In the series: Note 7.
Subject: The ex and ln(x) functions.
Date : 4 March, 2016Version: 0.3
By: Albert van der Sel
Doc. Number: Note 7.
For who: for beginners.
Remark: Please refresh the page to see any updates.
Status: Ready.
This note is especially for beginners.
Maybe you need to pick up "some" basic "mathematics" rather quickly.
So really..., my emphasis is on "rather quickly".
So, I am really not sure of it, but I hope that this note can be of use.
Ofcourse, I hope you like my "style" and try the note anyway.
Preceding notes:
Note 1: Basic Arithmetic.
Note 2: Linear Equations.
Note 3: Quadratic Equations and polynomials.
Note 4: The sine/cosine functions.
Note 5: How to differentiate and obtain the derivative function .
Note 6: Analyzing functions.
This note: Note 7: The ex and ln(x) functions.
Each note in this series, is build "on top" of the preceding ones.
Please be sure that you are on a "level" at least equivalent to the contents up to, and including, note 6.
This note will be a very small note on the subjects of the ex and ln(x) functions
It is important for one of the next notes (note 10).
Note 8 will have as it's main topic of finding "primitive functions". Then, note 9, is a very light touch
on "complex numbers". Next, note 10 will focus on "differential equations", and indeed,
especially the function ex often plays an important role as a solution.
1. Introduction "ex".
There are some numbers with a "sort of" special status, like '0', or '1', or π (as we have seen in note 4), or "e".The number "e" is close to about '2.7', but you can try to calculate as far as you can, the fraction (behind the dot, or comma),
but it never ends.
As a "reasonable" aproximation, the number 2.71828 is often used in many calculations.
I must take care not to dwell on the number itself, since it takes too much time. However, I can tell you that
for physicists (like me), "e" is an "old friend", which is present in a awful lot of equations in physics.
The number which is named "e", is also known as the number of "Euler", and maybe it's nice to Google on
"significance of euler's number", on a rainy Sunday.
1.1 A few remarks on general exponential functions in the form f(x)=bx.
We by now have seen quite a few types of functions, like linear-, and quadratic functions, polynomials of higer degree,the sin(x) and cos(x) functions etc..
Here we will meet a new class of functions, namely f(x)=bx, where "b" is some constant number (like '2').
These functions are easy to plot. In figure 1 below, I have plotted three examples, namely:
f(x)=2x (left side), and
f(x)=5x (middle), and
f(x)=0.3x (right side)
Figure 1. f(x)=2x, f(x)=5x, f(x)=0.3x
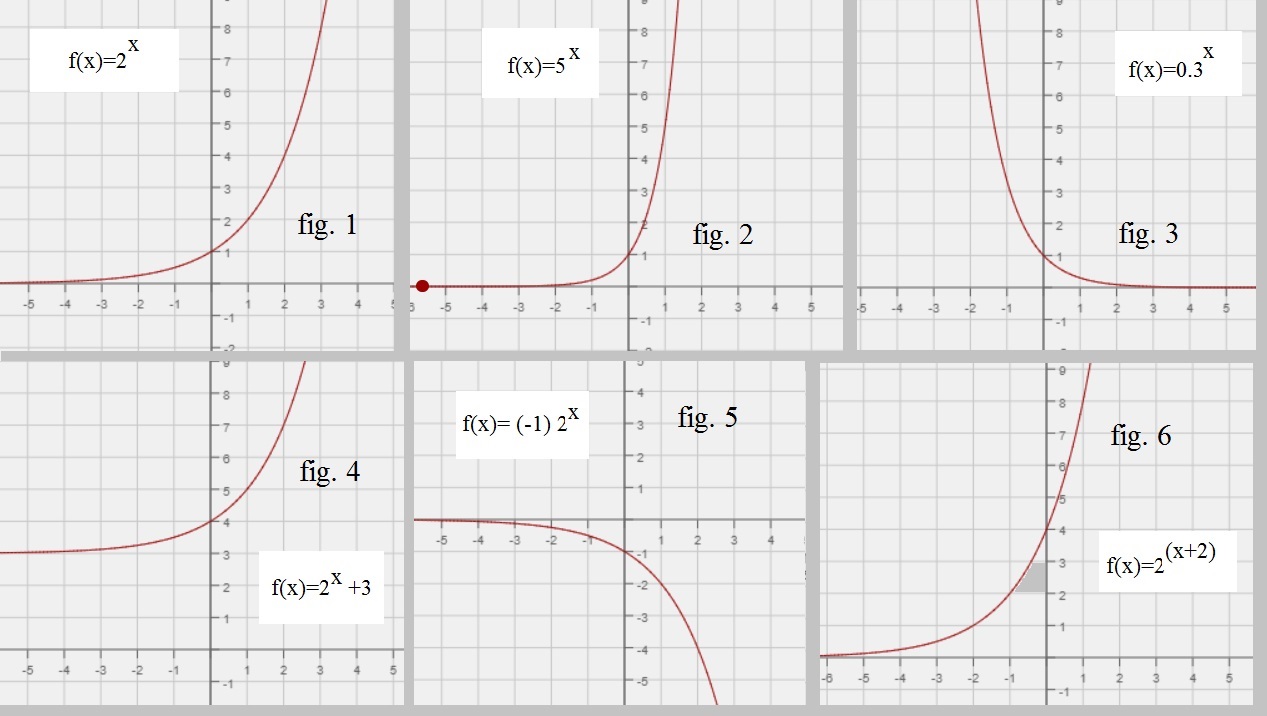
Le's concentrate for a moment on f(x)=2x and f(x)=5x. It's easy to plot them, since having
just a few points, already gives a reasonable picture on how the function "looks like".
Let's take a look at f(x)=2x
| value of x: | value of y=f(x) |
| x= -2 | y= 1/4, since 2-2=1/4 |
| x= -1 | y= 1/2, since 2-1=1/2 |
| x= 0 | y= 1, since 20=1 |
| x= 1 | y= 2, since 21=2 |
| x= 2 | y= 4, since 22=4 |
| x= 3 | y= 8, since 23=8 |
Question:
Can you make a similar table for f(x)=5x ?
Here are a few observations:
- If b > 1, then a fuction as f(x)=bx has a shape as we have seen above. However, the larger b is,
the faster the function "climbs". Suppose b=10, then when x=3, then f(x)=103 = 1000,
and when x=6, then f(x)=106 = 1000000.
- If 0< b < 1, then a function as f(x)=bx has a shape similar to the right curve in figure 1.
When x is positive (like 2, 3 etc..), the function decreases fast. For example, for f(x)=0.3x it holds,
that if x=2, then f(x)=0.32 = 0.3 x 0.3 = 0.09, and if x=3, then f(x)=0.33 = 0.3 x 0.3 x 0.3 = 0.027.
- Note that those functions exhibit aymptotic behaviour. They never reach the x-axis completely, but they get "nearer and nearer".
For a example, for an exponential function with b > 1, then when x approaches "-infinity", then f(x) approaches '0'.
Or, lim x → - ∞ f(x) = 0.
1.2 The exponential function f(x)=bx when "b"=e.
As as graph, f(x)=ex is quite similar to the graphs we have seen above (where b > 1).So, you might say that we have not much "news" here.
Figure 2. f(x)=ex
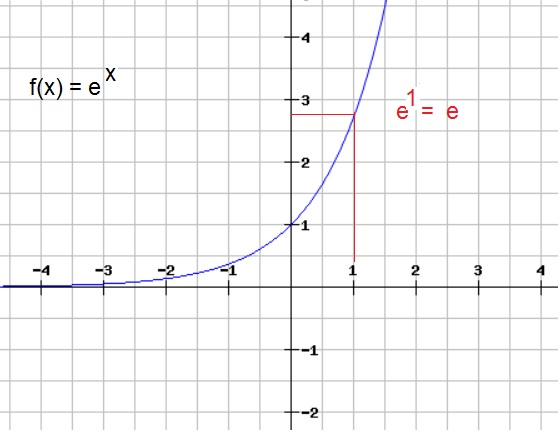
Ofcourse, when x=1, we have f(x) = e1 = e.
Note in figure 2, that e is about 2.7.
1.3 Some background on "e".
Around the year 1683, Jacob Bernoulli found that as "n" goes to infinity in the following expression,
the outcome "converges" to a very specific number. Today we call that specific number 'e'.
lim n → ∞ (1 + 1/n)n = e.
So, if you would say: let's take n=100, then the expression would be (1 + 1/100)100
Let's do some calculations. If you would calculate (1 + 1/10)10 then we have 2.59.
if you would calculate (1 + 1/100)100 then we have 2.70.
You see, if we only take n=100, then we are already pretty close to the "true" 'e'.
You get more and more closer, the larger 'n' is.
People with a background in economics or accounting would see a rather familiar formula.
It resembles the formula when you set away an amount of money, to a certain rate of interest, for period of "t" (n).
The formula "(1 + 1/n)n" seems to be fundamental to describe a sort of accumulated growth with a constant interest rate.
Yes, but what about physics? Just too much examples are available. Here is one that that also resembles the above.
Suppose you have N0 particles of radioactive material. Each nucleus has a certain "chance" to decay. But as a statistical ensemble,
which is a very high number of such nuclei, each have a (general) expectation value to decay.
Say that this expectation value is 6 hours, and you single out one of such nuclei, then there still is a chance
that you stare to it for several years. But on average, each nuclei has a good chance to decay in about 6h.
The "half-life" is defined to be that time, that halve of the material has decayed (with a very high probability).
The amount of original (not decayed) nuclei, can be described by:
N(t)= N 0 e -kt
In this case the e -kt factor, resembles the utmost right curve in figure 1 a bit, as of x > 0.
Many natural processes can be described using expressions, where 'e' plays a major role, especially at
all sorts of events where an "ensemble" growths or diminishes.
What is that with "e"? I don't think it's only math or physics. I bet that it's a matter for philosophy too.
2. Introduction "ln(x)".
2.1 Inverse function in general.
Suppose you have the functions u and v, in such a way, that u(v(x)... is x again !Well, it's not uncommon to have such functions. Suppose we have these two:
u(x)=√ x
v(x)=x2
Then u(v(x)= √ (x2) = x.
So, if we let "v" operate on x first, en then let "u" operate in "v(x)", we have x again. So, if both functions
are applied, then nothing happens to "x". The funcion "u(v(x)" maps "x" onto itself.
If we look at these two again:
u(x)=√ x
v(x)=x2
Then people also often say, that "v" is the inverse function of "u", and the other way around.
When two functions are related in such a way, people often do not talk of 'u" and "v" functions,
but the use the f anf f-1 notation.
Thus: f(f-1(x)) = f-1(f(x)) = x
The functions "f" and " f-1" are both each others inverse function.
Note: (optional reading)
In other mathematical disciplines, like that of studying vectors, matrices etc.., when a "mapping" or "operator" A
has an inverse operator, A-1, then it is often said that "A A-1 = I",
where I is the Identity operator, or "the doing nothing" operator, which nicely sums it up.
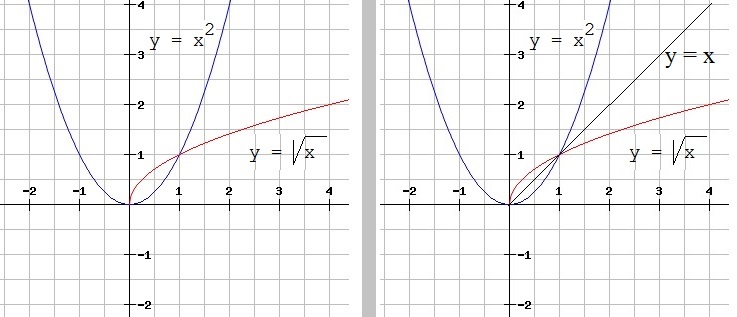
Let's plot both √ x and it's inverse x2 in the XY plane.
See figure 3. Note that if you would also plot the line "y=x", then it becomes visible that both functions
are "mirrored" through "y=x".
Ofcourse, when we say "x is mapped onto itself", it means the line y=x, since that function is f(x)=x,
thus for example f(f-1(x))=x, means that f(f-1(x)) really is the same as y=x.
Figure 3. x2 (in blue) and √x (in red) x
2.2 ln(x) as the inverse function of ex.
Another class of functions are the logarithmic functions. In many technical applications and stdies,the logarithmic function using the number '10' as it's "base", is very helpful.
A couple of examples may illustrate that.
The "claim" here, is that if g(x)=ex, then it's inverse function is h(x)=ln(x).
But, if that is true, then h(x)=ln(x), must be the inverse function of g(x)=ex.
We know how the the curve of ex looks like. Then, the inverse function must be the mirror with respect to f(x)=x.
Indeed, ofcourse it's possible to draw such an inverse curve, since you only need to mirror ex in f(x)=x.
Sure, it would be great to prove it. However, I can't prove it right now, since I like to do that using a primitive function.
Figure 4. g(x)=ex and h(x)=ln(x)
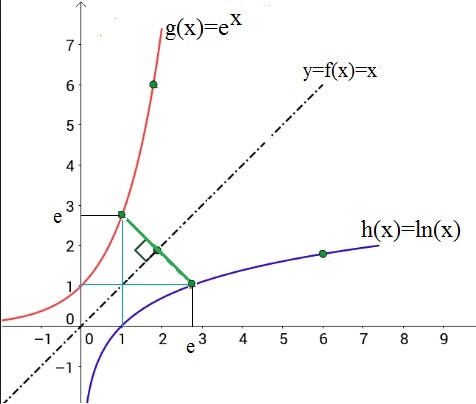
Thus, if they are each others inverse, then it should be true that:
ln(ex) = e ln(x) = x
2.3 The derivatives of ln(x) and ex.
Ofcourse we need to know the derivatives of both functions.1. The derivative of ex:
From note 5, we know that the fundamental relation for "the rate of change" is:| lim h -> 0 | f(x + h) - f(x) ---------------- h |
It's important to know, that the upper equation really is the "heart" of finding derivatives.
If needed, please check note 5 again, where the relation is fully explainend.
Now, using "ex" in the equation:
| lim h -> 0 | e(x + h) - ex ---------------- h |
Remember from note 1, that an+m = an am, where a can be any number.
Thus:
| lim h -> 0 | ex eh - ex ---------------- h |
Now, we can "factor out" ex:
| lim h -> 0 | ex (eh - 1) ---------------- h |
So, we may write that as:
| ex lim h -> 0 | (eh - 1) ------------ h |
Note: Do you see that we have managed to pull out ex from the Limit?
While the Limit itself converges to "1" (I should have proved that too), we have found the very remarkable fact, that:
If f(x)= ex then
f '(x)= ex
or:| ∂ ex ------ ∂ x |
= ex |
This fact, that the derivative of a function is itself, has amazed countless mathematicians and philosophers.
Indeed. It's a very remarkable fact. But we also know that ex is involved in accumulated natural growths
So, it might be argued, that it's very remarkable status, should not surprise us at all.
2. The derivative of ln(x):
Here we do not provide for a proof. I'am afraid to "clutter up" my notes too much, while they are intendedfor "quick" introductions in math. But I really like you to remember the following:
If f(x)= ln(x) then
f '(x)= 1/x
or:| ∂ ln(x) ------ ∂ x |
= 1/x |
Note that the function 1/x, shows asymptotic behaviour if "x" approaches "0".
We have seen 1/x before, so we were already aware of that fact.