This note is especially for beginners.

Maybe you need to pick up "some" basic "mathematics" rather quickly.
So really..., my emphasis is on "rather quickly".

So, I am not sure of it, but I hope that this note can be of use.
Ofcourse, I hope you like my "style" and try the note anyway.

Chapter 1. Introduction "Matrices":

1.1. Introduction "Vectorspace":

In "somewhat" more formal literature, you will encounter the term "vectorspace".
There exists a rather formal definition for it.

There is nothing to worry, since that definition is perfectly logical (if you have read note 12).

We already have seen some examples of vectorspaces, like the vectors in R³.
So we already seen them before. However, it is good to see also a formal description.
Now, a vector can be written in a row format (like e.g. (1,0,-2)) or column format.

The elements of a vector are just numbers (like the "-2" above). But in a formal definition, people say
that those elements are from a (scalar) field "K", which is just a number space, like the set of "real numbers".

Formal description:

A vectorspace "V" over the field "K" is a set of objects which can be added, and multiplied by elements of K
in such way that the sum of elements of V, is again an element of V (a vector), and the product of an element
of V by an element of K is again an element of V, and the following properties are satisfied:

Given that u, v, w are elements of V (vectors), and λ and μ are elements of K (scalars):

1. (u+v)+w = u+(v+w)
2. 0+u = u+0 = u  (where "0" is the nulvector, like for example (0,0) or (0,0,0) etc...
3. u+(-u) =0
4. u+v = v+u
5. λ (u+v) = λ u + λ v
6. (λ + μ) v = λ v + μ v
7. (λ μ) v = μ (λ v)
8. 1 v = v  (where "1" is simply the scalar "1")

These 8 properties of "V" will not really amaze you. For most properties, we have seen examples in note 12.
Let me recapitulate one. Say, number 4.
Suppose we consider the vectorspace R³. Suppose we have the vectors A and B, like:

A =	┌ a1 ┐ │ a2 │ └ a3 ┘

B =	┌ b1 ┐ │ b2 │ └ b3 ┘

Then A + B = B + A, which can be made plausible (or proven) by:

A + B =

┌ a1 ┐ │ a2 │ └ a3 ┘

+

┌ b1 ┐ │ b2 │ └ b3 ┘

=

┌ a1 + b1 ┐ │ a2 + b2 │ └ a3 + b3 ┘

=

┌ b1 + a1 ┐ │ b2 + a2 │ └ b3 + a3 ┘

=

B + A

1.2. What is a "Matrix"?:

A matrix is an (rectangular) "array" of numbers. It has "m" rows, and "n" columns.
In many applications, we have m=n, so the number of rows is equal to the number of columns. In that case, it's a "square" matrix.

Here is an example:

Figure 1. Example MxN matrix ("m" rows, and "n" columns)



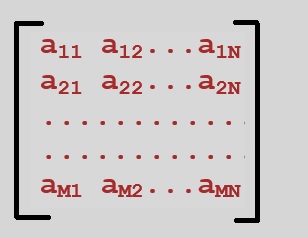
Do not forget that the "elements" like a₁₂, in the matrix, are just numbers, like for example 1, -5, 27.344, π etc..

Ofcourse, a matrix is not "just" an array of numbers. It must have a "real" meaning to it.
I am going to make it plausible for you, that a Matrix can be interpreted as:

Listing 1:

1. An object that determines and describes all the coefficients of a set of linear equations.
2. A "mapping" (or Operator, or Linear Transformation) on vectors.
3. That it can represents a tensor (in some fields of math or physics).

That a matrix can be identified as a linear "mapping" (sort of function on vectors), is probably
the most common idea on matrices.

Note:
In professional literature, scientists often use a sort of "shortcut" notation for a matrix.
Instead of the large rectangular array, they might simply write the matrix as:

  a_ij

where it is "implicitly" assumed (or clear) that we know that i "runs" from "1 to m", and j "runs" from "1 to n".
I will not use it much, but as you might see, it's a great way not to have the trouble of writing down such a "large object"
as a N x M matrix, like in figure 1. Saves a lot of time and effort.

Besides that we are going to understand how to interpret matrices, we ofcourse will do some great excercises too.

1.3 The matrix as a "coefficient matrix" of a set lineair equations

Example: coordinate transformation.

I'am going to use a "famous" problem here: a coordinate transformation. The discussion will show that a matrix is indeed
a "mapping", as well as that you can interpret it as an object that determines all the coefficients of a set of linear equations.

Suppose we have a vectorspace "V" of dimension "n". Then we need "n" independend basisvectors (or unit vectors),
in order to be able to describe any other vector.
It's quite the same as we already saw in note 12 (if needed, revisit note 12 again).

But actually we can have multiple (unlimited) of such sets of basisvectors. Suppose that we look at the familiar R³ space.
Then it's quite common to take (1,0,0), (0,1,0), and (0,0,1) as such basisvectors.
But this is not the only possible set. Just imaging that you "rotate" all axes (x-, y, and z-axis) over π/2 degrees
in some direction. Then, you can see that there is another set of unit vectors, tilted by π/2, compared to our first one.

So, suppose we have the following two sets of unit vectors of V:

Listing 2:

Β = {v₁, v₂, .. ,v_n}

Β' = {w₁, w₂, .. ,w_n}

Then each w_i can be viewed as an ordinary vector in the set Β, and thus can be expressed
as a linear combination of the v₁, v₂, .. ,v_n basis vectors.
In fact, we thus obtain a "set of linear equations".

Listing 3:

w₁ = a₁₁v₁ + a₁₂v₂ + .. + a_1nv_n
..
..
w_n = a_n1v₁ + a_n2v₂ + .. + a_nnv_n

All those coefficients a_ij form a square nxn matrix.

Figure 2. the NxN matrix that belongs to listing 3.



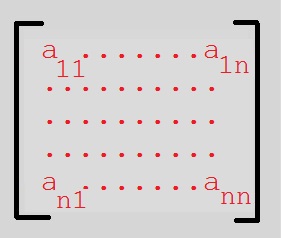
So, the coordinate transformation (which is a mapping too) of our example above, leads to a set of linear equation,
and we can have all coefficients of that set, correspond to a Matrix.

1.4 The matrix as a "Mapping" or Linear Transformation

This chapter is ony an introduction. I want to establish a certain "look and feel" at an early moment.
A more thourough discussion follows at a later moment.

We can multiply an n x n matrix with an 1xn Column Vector.
It will turn out, that in many cases we can identify that multiplication with a "mapping", meaning
that a vector will be mapped to another vector.

I must say that the statement "We can multiply an n x n matrix with an 1xn Column Vector" is not
a universal enough. As we will see, we can multiply a "MxN" matrix with a "NxS" matrix, leading to a "MxS" matrix.
Note how general such statement is. The results could thus also return a column or row vector,
which in many cases can be identified as a mapping too.

We must make that "plausible" ofcourse, meaning that the statements really make sense.

However, for the moment, please take notice of the following two statements:

Statement 1: general multiplication

M x N . N x S => leads to a M x S matrix It's quite easy to remember, since the result matrix uses the "outer" indices (m and s) only.
It will be proven at a later moment.

Statement 2: two special cases.

2.1 A 3x3 matrix and a column vector (1x3):

Let's explain how it's done. Each element of each row of the matrix, starting with the first row, is multiplied
with the elements of the column vector. This should be quite easy to remeber too.
Note that the operation leads to another column vector.
We can identify such matrix as a Linear Transformation on objects in R³, so in general we speak of a R³ -> R³ mapping.

2.2 A 2x2 matrix and a column vector (1x2):

┌ a b ┐ └ c d ┘

┌ x ┐ └ y ┘

=

┌ ax+by ┐ └ cx+dy ┘

=

┌ x' ┐ └ y' ┘

It's quite the same as 2.1, however here we can see a R² -> R² mapping.
Note that here too, the result of the mapping is a vector again.

Examples:

Let's try a few examples of the procedure of 2.2:

Example 1:

┌ 3 0 ┐ └ 0 3 ┘

┌ 1 ┐ └ 2 ┘

=

┌ 3*1+0*2 ┐ └ 0*2+3*2 ┘

=

┌ 3 ┐ └ 6 ┘

So, in this example, the vector (1.2) is mapped to (3,6).
Actually, this will happen with any vector in R². So, this mapping is a sort of "scaling" operator,
"enlarging" any vector by "3".

Example 2:

You do not need to "verify" or something, the following mapping.
Let's again stay in R². If we have any vector (x,y), then a clockwise rotation
of the vector over an angle ϕ, can be expressed by:

┌ cos(ϕ). sin(ϕ) ┐ └ -sin(ϕ) cos(ϕ) ┘

┌ x ┐ └ y ┘

So, if indeed would have a particular vector, say (1,2) or any other, and you know the angle ϕ,
then you can calculate sin(ϕ) and cos(ϕ). Then using the general procedure as shown in 2.2,
allows you to calculate the result vector.

Remember, the main purpose of this chapter, is to give you a pretty good idea on the several interpretations
of matrices (as was shown in listing 1 above). And at this point, real "calculations" are not important.

1.5 Matrices and Tensors.

Maybe it's not appropriate to say something on tensors at this stage, but I like to try
to provide a good overview on matters.

As it is now, we have scalars, vectors, and matrices.

-scalar: just a number, like the temperature at points in space.
There is no "direction" associated with scalars.

-vector: an object with magnitude (length) and direction.
Many physical phenomena can be expressed by vectors, like an Electric field,
which has a certain magnitude at points, but a "direction" as well (e.g. a positively charge partice moves along the field).

-Matrix: It's probably best to associate it with an "operator", or "linear mapping".

Well, it's math so take stuff seriously. However, not too "strickt"....

You can easily say that some scalar, is an operator as well. Just look at this:

5 *

┌ 3 ┐ └ 2 ┘

=

┌ 15 ┐ └ 10 ┘

Here the scalar "5" looks like a (linear) operator... and here it really is.

Now, about tensors. Tensors have a "rank". A tensor of rank 2, can be identified as a matrix.

You know that a matrix is characterized by it's elements. We generally have a mxn Matrix,
with m rows and n columns. We need two indices, to run over all m and n.

So, with a_ij=a₂₃ we indentify the element in the second row, the third column.

But tensors exist with even a higher rank, for example rank 3.

Some structures in physics, can only adequately be described by a rank 3 tensor.
For example, SpaceTime. Einstein described gravity, as the result of curved SpaceTime.
He extensively used higher rank tensors in the theories.

But we can stay closer to home as well. Suppose you have some material, like a block of metal.
I you apply a torque at both ends, then the inner "twist" of directions that the material feels,
is so complex that you need a sort of a_ijk mathematical object, to describe it mathematically.

But wait, we can only have mxn matrices, described by elements a_ij. So clearly, an a_ijk tensor
is really beyond a normal mxn matrix.

For tensors (in physics), ijk indices can be used, but more often, physicists like indices as μ, ν η.
So, in professional literature, you may see a third rank tensor as T_η^{μ ν} or T^{μ ν η}.

A third rank tensor may be visualized as a "stack" of a_ij matrices, or better, as a cube.
For higher rank tensors, we cannot visualize it anymore. We can only do math with them.

The figure below, might give an impresson on a (second rank) matrix, and a third rank tensor.

Keep in mind, the nxm does not determine the rank of a true matrix: it's rank is always 2 (or 1 in case
of a 1xn or nx1 matrix, where you only need one index).

So, even if you have a 8x10 matrix, you still have only 2 indices, "i" and "j". Indeed, you still only have to deal
with rows and columns. A matrix will always resemble a part of a spreadsheet if you like.

Only a rank 3 tensor, or higer rank tensor, needs more than 2 indices to describe the elements.
A rank 3 tensor, looks like a "cube", or stack of matrices, where thus one extra index is required.

The above text, is kept rather general, and indeed, there are some special exceptions.

Figure 3. Comparing a second rank tensor (or matrix), with a third rank tensor.



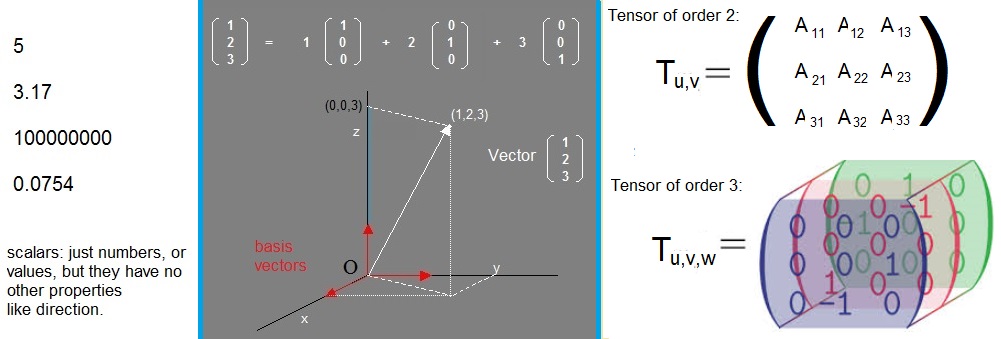
The next chapter deals with further properties of matrices, and matrix calculations.

Chapter 2. Properties of matrices, and calculating with matrices:

If we see a matrix operating on a vector, no matter what the dimension the Vectorspace is,
like for example:

┌ a b ┐ └ c d ┘

┌ x ┐ └ y ┘

=

┌ x' ┐ └ y' ┘

Then we will often use the following condensed notation:

AX = X'

Where A is the matrix, X is the original vector, and X' is the (mapped) resultvector.

Next, we will see a listing of short subjects, all of which are important in "vector calculus" or "linear algebra".

1. Multiplication of a matrix with a scalar:

Suppose A is a matrix, and λ is a scalar (a scalar is just a number).

Then: multiplying the matrix with λ, means multiplying each element a_ij with λ.
So, for example for a 2x2 matrix:

A =	┌ a b ┐ └ c d ┘

then λ A would yield:

λ A =

┌ λa λb ┐ └ λc λd ┘

2. Addition of matrices:

This is only defined and meningful, if both are of the same "size", thus both are "mxn" matrices, with the same "m" and "n".
So both have the same number of columns and rows, like for example "3x3" or "2x4" or "2x5" etc...

Suppose:

A =	┌ a11 a12 a13 a14 ┐ └ a21 a22 a23 a24 ┘

B =	┌ b11 b12 b13 b14 ┐ └ b21 b22 b23 b24 ┘

Then:

A + B = B + A=

┌ a11+b11 a12+b12 a13+b13 a14+b14 ┐ └ a21+b21 a22+b22 a23+b23 a24+b24 ┘

3. The Identity Matrix:

This special "square" nxn matrix, will have all a_ij=0, except voor those a_ij where i=j. If i=j, then a_ij=1
In effect, only the diagonal elements, from the upper left to the lower right, will be "1".
We will see that this matrix, maps a column vector onto itself. In effect, the matrix does "nothing".
Hence the name "Identity matrix", often denoted by "I".

Here the 3x3 "Identity matrix":

I =	┌ 1 0 0 ┐ │ 0 1 0 │ └ 0 0 1 ┘

The 2x2 "Identity matrix" is this one:

I =	┌ 1 0 ┐ └ 0 1 ┘

Let's perform an operation with 3x3 "I", on the column vector "X"

IX =

┌ 1 0 0 ┐ │ 0 1 0 │ └ 0 0 1 ┘

┌ x ┐ │ y │ └ z ┘

=

┌ 1x+0y+0z ┐ │ 0x+1y+0z │ └ 0x+0y+1z ┘

=

┌ x ┐ │ y │ └ z ┘

So, "I" maps the vector onto itself, and the result vector is the same as the original vector.
You may wonder why it is neccessary to mention "I" at all. Well, It can help to understand the "inverse" matrix A^-1 of matrix A.

Note:
In some articles you may also see the "Kronecker delta" notation for the Identity matrix, using the δ_ij symbol.
Using this notation, it is understood (or actually agreed upon), that:

δ_ij = 0 for i <> j, and
δ_ij = 1 for i = j.

4. The Inverse Matrix:

If the matrix "A" can be identified as a "mapping" (or transformation), then generally we may write:

AX = X'

In many cases, the mapping A has an "inverse" mapping A^inv, or also notated as A^-1,
which is the precise opposite mapping of A.

Suppose that A is a clockwise rotation of vectors in R² over some angle ϕ.
Then A^inv is the counter-clockwise rotation over that same angle ϕ.
When you apply A, and next A^inv, a vector is again mapped onto itself.

For a mapping A and it's inverse mapping A^inv, it holds that:

AA^invX = X

or:

AA^inv = I

So if you apply A (on some source vector), and then apply A^inv, then the result is that you have the original again.

5. Viewing the rows and columns of a Matrix, as vectors:

We have seen quite a few nxm and square nxn matrices by now.

Sometimes, it can be handy to view the "n" columns of the matrix, as "n" columnvectors.
And, likewise, to view the "m" rows of the matrix, as "m" rowvectors.

There are some good reasons for viewing a matrix that way, in some occasions. For example, suppose that you see
that for a certain matrix, the columnvectors are not independent (like the second column is just equal to a scalar times the first column),
then the are implications for the "mapping" that this matrix represents.

A =	┌ a11 a12 a13 ┐ │ a21 a22 a23 │ └ a31 a32 a33 ┘

Then sometimes it's handy to take a closer look at the column vectors of A.

For example, are the following vectors:

┌ a11 ┐ │ a21 │ └ a31 ┘

,

┌ a12 ┐ │ a22 │ └ a32 ┘

,

┌ a13 ┐ │ a23 │ └ a33 ┘

independent? That is, is one vector not just a "multiplication" of a number with another vector?

In chapter 3, we will appreciate this better.
For now, the only thing that I like to say here, is that we can also view a matrix as a set
columnvectors, or rowvectors, which may give us some extra insights on several occasions.

6. The Transpose of a Matrix:

If you have any mxn matrix A, then if you simply interchange all the rows and columns,
you get the transpose matrix ^tA.

Example:

Suppose that matrix A is:

A =	┌ 2 1 0 ┐ └ 1 3 5 ┘

Then the transpose Matrix "^tA" is:

tA =	┌ 2 1 ┐ │ 1 3 │ └ 0 5 ┘

There are several reasons why the transpose matrix is defined. One of which we will see later on.

One reason we will see here now: if a nxn matrix is "symmetric" with respect to it's diagonal, then A = ^tA,
thus in that case, the matrix A is fully equal to it's transpose matrix.

Example of a symmetric matrix (neccessarily nxn ofcourse):

A =	┌ 2 1 5┐ │ 1 3 0│ └ 5 0 2┘

For that matrix, it is true that A = ^tA. You can easily check it by interchanging the rows and columns.

7. The Determinant of a Matrix:

For a square nxn matrix, you can calculate it's determinant. It's just a scalar, specific for that matrix,
using a certain calculation of the elements a_ij of that matrix.

This number, belonging to the matrix A, is denoted by either det(A), and often also by |A|.

For a 2x2 matrix, the determinant is calculated as in the example below:

A =	┌ a b ┐ └ c d ┘

Then:

det(A) = ad - bc

What use can we possibly have from calculating the determinant?

There are several properties of the matrix you can immediately deduce, once you have the determinant.
One important one is this: can we view the columnvectors of the matrix as being independent?

Consider this matrix:

A =	┌ 3 0 ┐ └ 0 3 ┘

Then |A| = 3*3 - 0*0 = 9.

Now, consider this matrix:

B =	┌ 1 2 ┐ └ 2 4 ┘

Then |B| = 1*4 - 2*2 = 0.

In the latter case, |B|=0. If you look more closely to the columnvectors of matrix B,
then those two vectors are not independent.
Here we can see that:

┌ 2 ┐ └ 4 ┘

=

2*

┌ 1 ┐ └ 2 ┘

So, those two columnvectors are not independent.
If the det(A)=0 for some matrix A, then we know that the columnvectors are not all independent,
which can be important in certain occasions (see chapter 3).

Chapter 3. More on Linear mappings or Linear transformations:

It's true that many subjects in physics, can be described by what is called "a linear mapping".

We already have seen some examples, like the rotation of vectors in R² over an angle, which can
can be described by a matrix.

However, there also exist several classes of "non-linear mappings", which often are a subject in
more advanced notes.

The definition of a Linear mapping or Linear transformation is certainly not difficult.
We will see it in a moment.

In a somewhat more formal description in linear algebra, folks speak of vectorspaces "V" and "W",
where both can have any number of dimensions.

We often, "silently", assumed that we were dealing with a mapping from e.g. R² -> R², or R³ -> R³ etc..
However, exploring mappings from e.g. R⁴ -> R², are very common subjects in linear algebra.

So, when a formal description talks of vectorspaces "V" and "W", you ofcourse may think of examples like R³ -> R³,
or simply go with the general formulation using the V and W vectorspaces.

3.1 What is a Linear Transformation?

Let V and W be vectorspaces over the field K.
Let the vectors u and v be members of V (that is: u and v ∈ V).
Let λ be an element of K.

A linear mapping F: V -> W is a mapping with the properties:

F(u + v) = F(u) + F(v)

F(λv) = λ F(v)

Note that V -> W might thus also be V -> V (like R³ -> R³).

These are pretty simple rules. In a interpretation from physics, one might say that the mapping has no bias
for a certain direction in the vectorspaces.
You might also say that you see some "associative" and "distributive" properties here.

As an example of property 1:

Suppose we have a rotation operator A.

Method 1:
Let's first add two vectors u and v in the usual way. This will yield result vector w = u + v.
Next, we let the rotation operator work on w. This will yield w'.

Will this be the same as the following sequence of events?

Method 2:
Let the rotation operator first work on u and v. This will yield the result vectors u' and v'.
Then we will add u' and v', resulting in w' = u' + v'.

Does both methods result in the same w' ? If so, then A is a linear mapping.

Let's try it, using a simple example.

Let the mapping A have the associate matrix:

A =	┌ 0 -1 ┐ └ 1. 0 ┘

This is a counter clockwise rotation over 90 degrees. Yes, I indeed choose a simple one, but that does not matter at all.

Let the vectors u and v be:

u =	┌ 1 ┐ └ 0 ┘

v =	┌ 0 ┐ └ 1 ┘

Yes, these are the standard basis vectors of R², but that's OK too.

=> Let's do method 1 first.

Adding u and v results in the vector w = (1,1).
Next, let A operate on w:

Aw =

┌ 0 -1 ┐ └ 1. 0 ┘

┌ 1 ┐ └ 1 ┘

=

┌ -1 ┐ └ 1. ┘

=> Next we do method 2:

Au =

┌ 0 -1 ┐ └ 1. 0 ┘

┌ 1 ┐ └ 0 ┘

=

┌ 0 ┐ └ 1 ┘

Av =

┌ 0 -1 ┐ └ 1. 0 ┘

┌ 0 ┐ └ 1 ┘

=

┌ -1 ┐ └ 0. ┘

So:

Au + Av =

Aw =

┌ 0 ┐ └ 1 ┘

+

┌ -1 ┐ └ 0. ┘

=

┌ -1 ┐ └ 1. ┘

Yes, both methods work out the same way. So, in this particular example we have A(u+v) = A(u) + A(v)

3.2 A Linear Transformation and it's Matrix, and the mapping of the basis vectors.

Example of directly finding the matrix of some Linear Transformation:

Suppose we have a linear mapping F: R⁴ -> R².

Yes, this is from a 4 dimensional vectorspace (V) to our familiar 2 dimensional vectorspace (W).

Suppose further that the set of vectors {E¹, E², E³, E⁴} form a set of basisvectors in V.

Next, suppose that we know of the following mappings of F:

F(E1)=

┌ 2 ┐ └ 1 ┘

,

F(E2)=

┌ 3. ┐ └ -1 ┘

,

F(E3)=

┌ -5 ┐ └ 4. ┘

,

F(E4)=

┌ 1 ┐ └ 7 ┘

Then I immediately know the matrix that we can associate with F, namely

F =	┌ 2 3. -5 1 ┐ └ 1 -1 4. 7 ┘

I will make it plausible to you, how I came to this knowledge.

I will show you, that if you have a linear mapping "F", that then the mappings of the basisvectors, immediately
will show you the column vectors of the matrix of "F".

In fact, this is exactly what happened in the example above.
Let's try this in R³. Watch the following reasoning.

Suppose F is a "linear mapping" from R³ to R³.
So, we suppose that the matrix of F is:

F =	┌ a b c ┐ │ d e f │ └ g h i ┘

We further do not know anything of F, except that it is a linear mapping. Hence also the unknow elements in the matrix above.

In R³, we have the following set of orthonormal basisvectors:

┌ 1 ┐ │ 0 │ └ 0 ┘

,

┌ 0 ┐ │ 1 │ └ 0 ┘

,

┌ 0 ┐ │ 0 │ └ 1 ┘

Next, we let the matrix F operate on our basisvectors. I will do this only for the (1,0,0) basisvector.
For the other two, the same principle applies. So, this will yield:

┌ a b c ┐ │ d e f │ └ g h i ┘

┌ 1 ┐ │ 0 │ └ 0 ┘

=

┌ a*1+b*0+c*0 ┐ │ d*1+e*0+f*0 │ └ g*1+h*0+i*0 ┘

=

┌ a ┐ │ d │ └ g ┘

Well, this is indeed the first column vector of the matrix F.

So, one fact to remember is: the mappings of the basis vectors correspond to the column vectors of the matrix.

Chapter 4. Distances in Rⁿ (flat Eucledian space):

In another note, I will show hoe to deal with "distances" in non-Eucledian curved spaces, or using a different non-Cartesian
coordinate system. Then also "contravariant" and "covariant" vectors and indices will be discussed.
I think that this sort of stuff will go into note 18.

In this section, we going to discuss the "distance" between points in Rⁿ (like R² or R³).

You can view this stuff in multiple ways. You can say that we "just" have two points P and P', and the line segment
which connects those two points, clearly determines the distance between them.
You can also say that we have a vector P and vector P', and the length of the vector P-P',
simply is the distance.
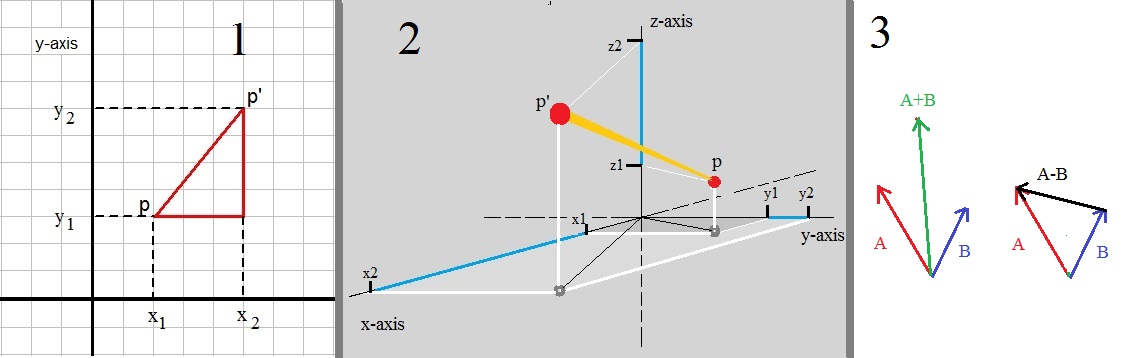
For about the last statement: take a look at figure 4, the third picture. Here we have vectors A and B, and the lenght
of the vector "A-B", defines the distance between the endpoints of A and B.

Figure 4. Some example distances.

In R²:

In figure 4, in the first picture, we have R² space. You can see that we have two points:

P : (x₁, y₁)
P': (x₂, y₂)   (note the accent on the "P")

We want to find the length of the segment PP'. Usually, the lenght of such a segment is denoted by |PP'|.

You can always "find" or construct a "right-angled triangle", when you have two points in R².

Here we can see that the lenght parallel the x-axis, is "x₂-x₁".
And that the lenght parallel the y-axis, is "y₂-y₁".

In our specific example in figure 4, we have x₂-x₁ = 5 - 2 = 3.
And for the y part, we have y₂-y₁ = 7 - 3 = 4.

Applying the "Pythagorean theorem", we find:

|PP'|² = (x₂ - x₁)² + (y₂ - y₁)²

Thus:

|PP'| = √ ( (x₂ - x₁)² + (y₂ - y₁)²) )

In R³:

For R³, we simply have one additional coordinate. So, we would have:

|PP'|² = (x₂ - x₁)² + (y₂ - y₁)² + (z₂ - z₁)²

Thus:

|PP'| = √ ( (x₂ - x₁)² + (y₂ - y₁)²) + (z₂ - z₁)²) )

In Rⁿ:

Suppose we have two points "P" and "Q" in Rⁿ, with the coordinates:

(p₁, p₂, .. ,p_n) and (q₁, q₂, .. ,q_n)

then:

|PQ|² = (p₁ - q₁)² + .. + (p_n - q_n)²)

Thus:

|PQ| = √ ( (p₁ - q₁)² + .. + (p_n - q_n)²) )

In general, a "distance", is quite often denoted by "S" or "s", so you may also use that in equations.

Note that a term like (p_n - q_n)² is equivalent to (q_n - p_n)².
This is so since the two have the same absolute value, but may differ in "sign" (+ or -). But, since we square it, the end result is the same.

Chapter 5. Intersections of lines:

Example of the "calculus" method in R²:

In note 2 (linear equations), we investigated how to find the "intersection" of two lines in R².
In R², if two lines are not "parallel", then they will intersect "somewhere".

In note 2, we used the following example:

Suppose we have the following two lines:

y= -3x - 3
y= -x - 1

At which point, do they intersect?

One thing is for sure: the point where the lines intersect, is the same (x,y) for both equations.
Thus we may say:

-3x + 3 = -x - 1   =>
-2x = -4   =>
x = 2.

Thus at the intersection, x must be "2". Now use one of both equations to find the corresponding y. Let's use "y= -x - 1" :

y = -x -1 => y = -2 -1 => y = -3.

So, the point where both lines intersect is (2,-3).

Example of the "vector" method in R³:

Since the dawn of mankind, or slightly later, it was already known that you only need 2 points to completely define a line.

Again we are going to see how to determine where (at which point) two lines intersect. However, this time we will use linear algebra.
The method shown here, works the same way in vectorspaces of all dimensions (e.g. R³, R⁴ etc...).

In figure 5 below, I tried to draw 2 lines in a Cartesian coordinate system (R³).
Hopefully, you can see a green line and an orange one.

Figure 5. Example lines in R³ (2 points A and B is enough to describe any line)



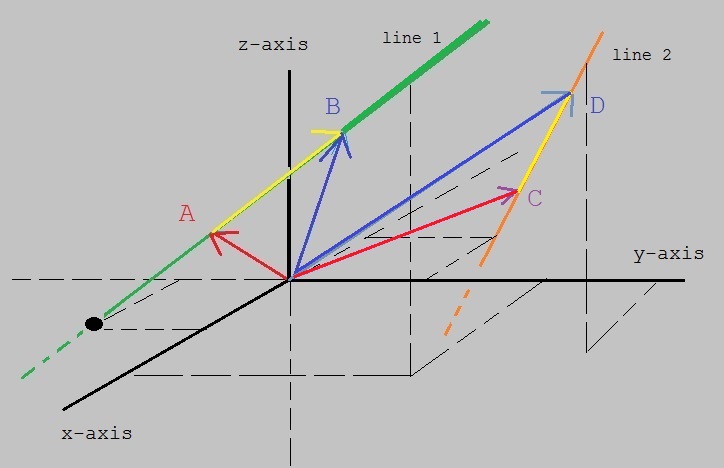
-Let's focus on the green line for a moment.

Say that we have two points on that line, A and B. Then we also have the vectors A and B,
depicted as arrows, originating from the origin.
By the way, it does not matter at all, where those two points are, as long as they are on that line.

You may wonder how we can write down an equation, by which we can "address" any random point (x,y,z) on that line.
Well, here it is:

┌ x ┐ │ y │ └ z ┘

=

A + λ (B - A)

It's just a matter of vector addition. The vector (B - A), is the yellow part, and lies on the line.
By varying the scalar λ, you can reach any point on the line (e.g. λ=0.3, or λ=5 etc...).

You should see it this way: use vector A, to "step" on the line, and then you can use λ(B - A) to reach any point on the line.

-Now, focus on the orange line.

A similar argument can be used, and we can "address" any random point (x,y,z) on the orange line line, by using:

┌ x ┐ │ y │ └ z ┘

=

C + μ (D - C)

Now, suppose in row vector notation, we have:

A = (a₁,a₂,a₃)
B = (b₁,b₂,b₃)
C = (c₁,c₂,c₃)
D = (d₁,d₂,d₃)

If the two lines really intersect, then at that point, we have the same x, y, z.

Thus, it must hold at that point, that:

A + λ (B - A)

=

C + μ (D - C)

If we write that out, we have a system of 3 linear equations:

a₁ + λ (b₁ - a₁) = c₁ + μ (d₁ - c₁)
a₂ + λ (b₂ - a₂) = c₂ + μ (d₂ - c₂)
a₃ + λ (b₃ - a₃) = c₃ + μ (d₃ - c₃)

Do not forget that the a₁, b₁ etc..., are simply known values, since we know the coordinates of A, B, C, and D.
The set of equations then boils down to resolving λ and μ, which is possible by substituting.
I am not going to work this out any further. For me, it's only important that you grasp the method of handling this problem.

I agree that solving the set of three linear equations is quite some work, but the method is generic for multiple dimensions.
Suppose we have the same problem in R⁴. Then only one extra coordinate is involved (for all 4 points),
but the principle really stays the same.

That's it. Hope you liked it !

The next note will explore some more advanced differentials like the Grad, Diff, and Curl operators.