In the series: Note 8.
Subject: Primitive functions or Integral functions.
Date : 5 March, 2016Version: 0.2
By: Albert van der Sel
Doc. Number: Note 8.
For who: for beginners.
Remark: Please refresh the page to see any updates.
Status: Ready.
This note is especially for beginners.
Maybe you need to pick up "some" basic "mathematics" rather quickly.
So really..., my emphasis is on "rather quickly".
So, I am really not sure of it, but I hope that this note can be of use.
Ofcourse, I hope you like my "style" and try the note anyway.
Preceding notes:
Note 1: Basic Arithmetic.
Note 2: Linear Equations.
Note 3: Quadratic Equations and polynomials.
Note 4: The sine/cosine functions.
Note 5: How to differentiate and obtain the derivative function .
Note 6: Analyzing functions.
Note 7: The ex and ln(x) functions.
This note: Note 8: Primitive functions or Integral.
Each note in this series, is build "on top" of the preceding ones.
Please be sure that you are on a "level" at least equivalent to the contents up to, and including, note 7.
This note will be a very short note on Primitive fuctions, and "integrals".
The "core" idea is really easy, as you will see in a minute.
1. Simple introduction of the expression ∫ab f(x) dx
It's not too hard to explain an expression like ∫ab f(x) dx.Although it might seem a bit awkward at first sight. But it really is only a representation
of a "summation" of very small "elements", as you will see below.
In the expression above, you see the function f(x). Suppose that this function is a continuous
and "well behaved" function. For example, there is no asymptotic behaviour for the "x interval"
for which we will study f(x).
Let's study f(x) in the interval x ∈ [a,b], that is, x "runs" in the interval from "x=a" to "x=b".
Now, let's see what f(x) does, when x "runs" in that interval. Especially, we like to estimate
the area between f(x) and the x-axis.
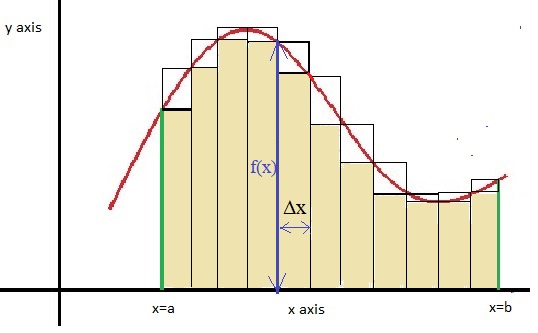
Take a look at figure 1 below. We see the function f(x) as the red curve. Also, we see the boundaries
defined from "x=a" to "x=b" (green vertical lines). Those boundaries, and the curve, determine the "area"
between the curve and the x axis.
Fig 1. The area defined by the boundaries x=a, x=b, and f(x).
For a rectangle with sides "b" and "h", we now that the area ("A") can be calculated as A=bh.
For a function as shown above, it cannot be that easy.
Well, actually, it will be quite the same procedure.
So suppose we divide the interval [a,b] into smal steps. Say that [a,b] is the range [1,9].
Then we could, for example, divide it in [1,2], [2,3], [3,4], [4,5], [5,6], [6,7], [7,8], [8,9].
Let's call such a smal interval like [2,3], Δxi. As you might know, the symbol Δ
is often used to denote a small interval, a sort of "delta" from a range of values.
For the example above, that is the set of [1,2], [2,3], [3,4],...,[8,9], each time
If you look at figure 1 again, you might agree that even that set of intervals, correspond to a set
of rectangles. The width of such rectangle is Δxi, and in this case, this is "1".
The height of such rectangle, then would be "f(Δxi).
So, the area defined by such rectangle would be A = Δxi f(Δxi).
If you would add all those up, that is add all those area's together, we could write it as:
AApproximation of the Area between f(x) and the x-axis = Σ i=1i=8 Δ xi f(Δxi).
Notice, that how smaller you would make such interval Δxi, the more accurate the sum would get.Ofcourse, if you would make Δxi smaller, then the number of intervals (let's call that "n"),
would get larger and larger.
Note: The Δ symbol, used to compactly write down a large summation. In this example: Σ i=1i=n ki,
it would mean the summation k1 + k2 + .. + kn, where each ki would be some number.
The area of f(x) to the x-axis in the interval a ≤ x ≤ b then can be approximated with:
approximation of the area = Σ i=1i=n Δxi Δf(xi) (equation 1)
If n would get very large, or what is the same, the Δxi's would get extremely small, then suchexpression can be written as shown below. It's just a matter on how you write things down. Thus:
∫ab f(x) dx = lim Δx ->0 Σ i=1i=n Δx f(Δx) (equation 2)
It's very important to understand that ∫ab is just another way to describe a summationas in the equation above. It's thus simply another way to write it down. It's just another way to put it on paper.
Only, Δxi would get infinitsemally small. That's all.
Note: if Δxi is really getting infinitesemally small, then it will be written as "dx".
In such case, the summation would have an extremely large number of elements. (going to infinite).
What we have established by now, is that the area between a function f(x) and the x-axis
where x runs from x=a to x=b, can be written as:
Area (between f and x-axis, from x=a to x=b) = ∫ab f(x) dx (equation 3)
Now, suppose that a very special function F(x) exist, for which would hold that:| f(x)= |
dF(x) ---- dx |
Or, F '(x)=f(x).
Or, f(x)dx=F '(x)
Remember from note 5 on derivatives, that a derivate function is also denoted by an accent " ' ".
If indeed a function F would exist, in such a way that F '(x)=f(x), then F is called the primitive function
of f(x). Also, an expression using ∫ f(x) dx, is called an Integral.
Now, I will show you how the area actually can be calculated, as is expressed in equation 3.
The area is:
Area (between f and x-axis, from x=a to x=b) = ∫ab f(x) dx = F(b) - F(a) (equation 4)
Here is my "proof":A mathematician would probably look very disturbed when he/she looks at my argument below.
However, my goal is: if I can make it likely for one good example, then you might accept the argument
to be "generally" true.
Example:
Suppose we have the line f(x)=2x. Figure 2 below, illustrates the graph of y=2x.
Fig 2. The area defined by the boundaries x=a, x=b, and f(x)=2x.
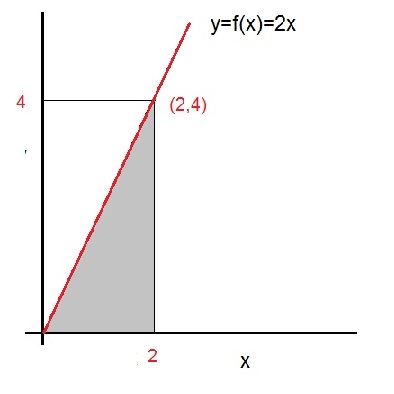
This line goes through the Origin of the XY plane (0,0), and also goes through the point (2,4).
You can probably see that a right-angled triangle exist, defined by the three points (0,0), (2,0) and (2.4).
This triangle is just exactly half of the rectangle with sidelengths 2 and 4.
So, the total surface area of that rectangle is 8, and thus for the right-angled triangle the Surface area is 4.
Thus: the area between f(x) and the x-axis where x runs from x=0 up to x=4, is "4".
Now, let calculate the integral. It should return the value 4 as well.
It's important to see that if f(x)=2x, then F(x) must be x2, since the derivative of F(x)=x2,
is f(x)=2x.
∫ 2x dx = x2
thus:
∫ab f(x) dx = F(b) - F(a) = F(2) - F(0) = 22 - 02 = 4
Indeed, the area is 4, just as we could see from the fact that the area of the right-angled triangle is exactly half
of the area of the rectangle defined by the points (0,0), (2,0), (0,4) and (2,4).
This reasoning will always work with linear equations of the form y=ax+b
Although ofcourse equation 4 is not proven, it is (hopefully) made likely and acceptable, by providing
just one simple example.
A key point is thus, to find F(x), if you only happen to know what f(x) is.
2. Primitive fuction: The indefinite integral ∫ f(x) dx.
Below we use the simple assumption that f(x) is a "well-behaved" function, with no gaps, and no asymptotes in the "neighborhood".Remember the "derivative" function, we saw in note 5? Here we found for example, that suppose we have f(x)=x2 + b.
Then the "derivative" function is f '(x)=2x.
In note 5, we also discussed some methods to calculate the "derivative", for several types of functions.
The interpretation of the "derivative" function was, that it described "the rate of change of f(x) : rate of change of x",
and therefore it determines the "slope", or gradient, of the tangent line to f(x), at "x".
This time, it's a bit the otherway around. Suppose we have f(x). Then what is F(x), in such a way that F '(x)=f(x)?
Example:
Suppose f(x)=4x3
Then, what is F(x)?
Answer:
F(x)=x4
Since the derivative of F(x) is F '(x)= f(x) =4x3
Here, you knew how to obtain the derivative of x4, which is 4x3
actually, "F(x)=x4 + c", where c is a constant. The derivative of a constant is zero.
Notation of finding the primitive (integral) function:
We introduce a new symbol, used in the equation of finding the primitive function, namely: ∫
Suppose we have funcion f(x). Then what is F(x), in such a way that F '(x)=f(x)? Thus f(x) is the "derivative" function of F(x).
∫ f(x) dx = F(x) + c
So, F(x) is called the antiderivative, or primitive function of f(x). It's just a way to write down stuff.Some rules (among many rules) of finding the primitive (integral) function:
- rule 1:
Suppose f(x)=xk
Then:
∫ xk dx = 1/(k+1) xk+1 + c
This is true since the derivative of 1/(k+1) xk+1 + c = xkThus F(x) = 1/(k+1) xk+1 + c
Again: Just think of for example the derivative of x3. The derivative is 3x2
Thus, the primitive of 3x2, is ofcourse x3.
You see how to interpret the "1/(k+1) xk+1" stuff?
Thus the derivative of 1/(k+1) xk+1 = (k+1) 1/(k+1) xk+1-1 = xk
- rule 2:
∫ a f(x) dx = a ∫ f(x) dx
where a is some constant.- rule 3:
∫ ( f(x) + g(x) ) dx = ∫ f(x) dx + ∫ g(x) dx
Example:Suppose h(x)=x5 + x3
Then what is the primitive function H(x)?
You can view h(x) as the sum of x5 and x3. So we can use rule 3, but rule 1 too:
H(x)=1/6 x6 + 1/4 x4
Indeed, you may say that we need to add a constant "c" too.It's true since the derivative of "1/6 x6 + 1/4 x4" is indeed "x5 + x3".
You see? The "core" idea is not hard to understand. But I agree that specific exercises can be quite spicy.
- rule 4:
Remember the "chain" rule from note 5?
It said that the derivative of the (compound) function f(x)=u(v(x)),
is f '(x) = u '(v(x)) . v '(x)
So..., it means that whenever you "reckognize" a function that "looks" like (or might be viewed as) u '(v(x)) . v '(x)
then it's primitive is u(v(x))
Doing many excercises will make you experienced in calculating primitives. For my purpose, understanding
the 'core' idea will suffice for the moment.
2. Integration over an interval "a ≤ x ≤ b": ∫ab f(x) dx.
This time, we will see an interpretation too. As we will see, integration over an interval meanscalculating the "area" below the function f(x) in two dimensions, like the XY plane.
Would we do a similar action in three dimensions, then we would calculate the "volume" bounded by some surface.
Later we will see more on the latter (not this note).
My statement now is, that in many cases:
∫ab f(x) dx = F(b) - F(a) = Area of f(x) in interval a ≤ x ≤ b
Ofcourse, it can be proved in a formal way. However, I like to provide an illustrative example.Example:
Suppse we have the line f(x)=2x.
This line goes through the Origin of the XY plane (0,0), and also goes through the point (2,4).
You can probably see that a right-angled triangle exist, defined by the three points (0,0), (2,0) and (2.4).
This triangle is just exactly half of the rectangle with sidelengths 2 and 4.
So, the total surface area of that rectangle is 8, and thus for the right-angled triangle the Surface area is 4.
Now, let's calculate the integral. It should return the value 4 as well:
∫ 2x dx = x2
thus:
∫ab f(x) dx = F(b) - F(a) = F(2) - F(0) = 22 - 02 = 4
So indeed. The integral returns the same value, as the Surface area we calculated before.Therefore, I hope that I made it "plausible" to be true in general as well.
If you believe that the example above is a representative example for a general case, then
we arrive as what is often seen as a "Fundamental Theorem of Integral Calculus":
∫ab f(x) dx = F(b) - F(a) = Area of f(x) in interval a ≤ x ≤ b
By the way, F(b) - F(a) is also sometimes denoted as [F(x)]abPlease remember that the indefinite integral (without the boundaries "a" and "b"), returns primitive functions.
And, the definite integral (over an interval) returns a value, to be intepreted as the Surface area below f(x).
Excercise:
Determine the definite integral of f(x)=2x3 -5, in the interval 1 ≤ x ≤ 3.
Answer:
We need to calculate:
∫13 (2x3 -5) dx
The primitive function of f(x)=2x3 -5, is F(x)=1/2x4 -5xThus:
∫13 (2x3 -5) dx = F(3) - F(1) = (1/2 * 34 - 5 * 3) - (1/2 * 14 - 5 * 1) = 30
Some more examples:
There are several methods to solve integrals.-learn basic primitives from tables (the standard functions and their primitives).
-investigate if it is possible to rewrite te integrand to something simpler.
-the method of "substituting".
-apply the "reverse differential" chain rule.
-the method of "integration by parts".
-know the most important goniometric and logarithmic identities.
-and other techniques.....
⇒ For some goniometric integrals, the following table may help:
| Rad | degrees | sin | cos |
| 0π | 0 | 0 | 1 |
| 1/6π | 30 | 1/2 | 1/2 √ 3 |
| 1/4π | 45 | 1/√2 | 1/√2 |
| 1/3π | 60 | 1/2 √3 | 1/2 |
| 1/2π | 90 | 1 | 0 |
1. Basic Examples:
Example 1:
In note 5 we found that:
If f(x)=sin(x) then f '(x)=cos(x)
If f(x)=cos(x) yhen f '(x)= -sin(x)
Thus:
∫ cos(x) dx = sin(x) + C
∫ sin(x) dx = -cos(x) + C
Example 2:
Suppose we have f(x)=x2(x-√x). What is F(x)?
In general, try to rewrite the expression, so to get rid of the "(" and ")".
This way, often it is easier to apply one of the rules listed above.
x2(x-√x)=x2x - x2√x = x3 - x2.5
Now we can apply our rules:
F(x)=1/4x4 - 1/3.5x3.5
This is the solution, but we need to rewrite it a bit more neatly:
1/4x4 - 1/3.5x3.5=1/4x4 - 2/7x3√x
F(x)=(1/4) x4 - (2/7) x3√x + c
Example 3: Two examples using "Simple substituting":
-Example 3.1:
Suppose we need to solve:
∫ (x-5)7dx
Call (x-5)=t.
Then our integral becomes:
∫ t7dt
Which is simple to solve, using our basic rules.
∫ t7dt = 1/8 t8 + C
Substituting (x-5)=t back, and our answer is:
F(x) = 1/8 (x-5)8 + C.
-Example 3.2:
Solve:
∫ 2x(x2+1)5dx
Rewriting the integrand will not help us much, that is, if you multiply the terms further, it gets very complex.
In example 2, the multiplication worked, but here it can be done in a more clever way:
Use t=(x2+1). Then dt=2xdx.
∫ 2x(x2+1)5dx = ∫t5dt=1/6 t6+C.
Substituting back:
F(x)=1/6 (x2+1)6 + C.
Example 4: Using chain rule:
In many cases, it's an alternative for the method of "substituting", and sometimes even simpler.
-Suppose we have f(x)=(2x+2)5. What is F(x)? This looks very similar to
what we had in Example 3.
Note that "2x+2" is a linear function.
You can see that something like (2x+2)6 puts us on the road. However, we still have the "2"
from the "2x" to deal with. So, if we try "1/12 (2x+2)6", would it work?
Using the chain rule for derivatives, we would then have "1/12 . 6 . (2x+2)5+1 . 2", which
gives us indeed (2x+2)5 again.
Note that what sits in the brackets, is linear, that is, of the form ax+b. With higher powers
of x in some terms, in the brackets, this method might need additional considerations.
- Suppose we have:
f(x)
=
x
-------- dx
(1+x2)3
Find the primitive of f(x). Note that you may also write f(x) as f(x) = x.(1+x2)-3.
We must somehow find a format, so that it fits the chain rule.
Note that d/dx (1+x2) = 2x.
Note that x = 1/2 . 2x
Note that the primitive of (...)-3, then must have a (...)-2 part.
It's not that we follow a very specific rule to get to our objective, but it might
be seen that F(x) = -(1/4) . (1+x2)-2
If you reckognize a function as f '(g(x)).g'(x), then the primitive is f(g(x)).
-Suppose we have f(x)=sin(2x). What is F(x)?
You always need a book of "tricks".
If you look at the derivative of cos(2x), then again using the chain rule, we have
-sin(2x).2 = -2sin(2x).
Thus:
F(x)=∫ sin(2x)dx =-1/2 cos(2x)+c
Here are a few important standard integrals with sin and cos:
∫ sin(ax)dx =-1/a cos(ax) + C (a is a constant)
∫ cos(ax)dx = 1/a sin(ax) + C
∫ sin2(x)dx =(1/2)x - 1/4 sin(2x) + C = (1/2)x - (1/2) sinx cosx + C
∫ cos2(x)dx =(1/2)x + 1/4 sin(2x) + C = (1/2)x + (1/2) sinx cosx + C
Example 5: More elaborate example of substituting:
Suppose we have f(x)=sin3(x). What is F(x)?
999First, note that sin3(x)=sin(x).sin(x).sin(x)=sin(x).sin2(x).
Now, in a former note we have seen that sin2(x) + cos2(x) =1.
Thus: sin2(x)=1-cos2(x).
So: sin3(x) = (1-cos2(x)).sin(x).
Now, d/dx (cos(x))=-sin(x). Thus d(cos(x))=-sin(x)dx.
Thus:
sin3(x)=(1-cos2(x)).sin(x)=(1-cos2(x)).-d(cos(x))
=(cos2(x) - 1)d(cos(x))
Now, we use the "substitution trick": u=cos(x).
Then we get:
(cos2(x) - 1)d(cos(x)) = (u2 - 1) du.
∫ (u2 - 1) du = 1/3 u3 -u +c
Thus:
∫sin3(x) = 1/3 cos3(x) -cos(x) +c
2. Examples with ex and exponential functions:
Example 6:
The derivative of ex, is ex. Therefore:
∫ exdx=ex + C
Example 7:
Let's try to find: ∫ ekxdx, where k is some constant.
Let's substitue u=kx. Therefore du=k dx. Thus (1/k)du=dx.
So, ∫ ekxdx = ∫ eu(1/k)du = (1/k)∫ eudu =(1/k)eu+C=(1/k)ekx+C.
Example 8:
Let's try to find: ∫ 2xdx. (this excercise is also model for ax)
If gLog(x)=y, then gy=x. Thus gLog(x)=x.
Thus:
eln(2)=2
∫ 2xdx = ∫(eln(2))xdx = ∫(eln(2) x)dx
Now, set u=ln(2)x. Thus du=ln(2)dx. Thus 1/(ln(2) du =dx.
Let's substitute that: ∫(eln(2) x)dx=1/ln(2) ∫eudu = 1/ln(2) eu +C.
Let's subsitute u=ln(2)x back:
1/ln(2) eln(2)x +C = 1/ln(2) (eln(2))x +C = 1/ln(2) 2x +C.
You can generalize this to: ∫ axdx = 1/ln(a) ax + C.
So, the method of "substituting" can be quite important, as we have seen in a few examples above.
3. Examples using the method of integration by parts:
The productrule from finding a derivative can be beneficial too, in finding the primitive function.
This rule is:
(f.g)' = f'.g + f.g' (note the apostrophes).
Thus:
f'.g = (f.g)' - f.g', and also f.g' = (f.g)' - f'.g
This means that:
∫ f'.g = ∫ (f.g)' - ∫ f.g' = f.g - ∫ f.g'
You may read this rule also as (to make it more clear):
∫ f.g = F.g - ∫ F.g' where F is the primitive of f, and g' is the derivative of g.
The difficulty is often to choose the most practical "f" and "g". Let's see some examples:
Example 9:
∫ x linx dx = 1/2 x2 lnx - ∫ 1/2 x2 . 1/x dx = 1/2 x2 lnx - 1/4 x2 + C.
Example 10:
∫ x sinx dx = -cosx x - ∫ -cosx . 1 dx = -xcosx - sinx + C.
Example 11:
∫ lnx dx = ∫ 1 . lnx dx = x lnx - ∫ x . 1/x dx = x lnx - ∫ 1 dx = x lnx - x + C
Example 12:
∫ x.ex dx = x.ex - ∫ ex . 1 dx = x.ex - ex + C.
4. Examples with fractions:
There are already a few facts that we know:
If f(x)= ln(x) then
f '(x)= 1/x
Thus if we have f(x)=1/x, then
F(x)=ln(|x|).
and, from example 11, we have seen that:
∫ lnx dx = ∫ 1 . lnx dx = x lnx - ∫ x . 1/x dx = x lnx - ∫ 1 dx = x lnx - x + C
Likewise:
∫ log(x) dx = 1/ln(g) . (x lnx - x ) + C
We might use that in some examples.
Example 13:
∫1/(2x+1) dx
set t=(2x+1). Thus dt=2dx. Thus dx=1/2dt
∫ (1/2) 1/t dt = 1/2 ∫ 1/t dt = 1/2 ln(t) = 1/2 ln(2x+1) + C
Example 14:
Suppose we have:
f(x)
=
4x4+4x3+x2+3
----------------
2x+1
Then ∫ f(x)dx seems a real challenge.
There are several ways to handle this. You might try a "tail divison".
2x+1 / 4x4+4x3+x2+3 \ 2x3+x 2 + x
---------4x4+2x3
---------2x3+x2
---------------------
---------2x2+x
with a remainder of "3".
This way, we have:
f(x)
=
4x4+4x3+x2+3
----------------
2x+1
=
2x3+x2+x+
3
----
2x+1
This way, we see that the integral
∫f(x)dx
=
∫ (
4x4+4x3+x2+3
----------------
2x+1
) dx
=
∫ (
2x3+x2+x+
3
----
2x+1
) dx
And we know how to handle each of those terms, including the 3/(2x+1) term (see example 13).
Example 15:
Sometimes, you can split the fraction in multiple terms.
Suppose we have:
∫f(x)dx
=
∫
x2+3
-------- dx
2x
We can split this into:
∫ f(x)dx
=
∫
x2+3
-------- dx
2x
=
∫
x2
--- dx
2x
+
∫
3
--- dx
2x
Where we can deal with both terms with the knowledge presented above.
5. Examples of more complex questions:
Example 16:
Suppose we have a bathtube, where the surface at any height x, is determined by:
C(x)=2500x0.5-70x (in cm2)
The max height of the bathtube is 50cm.
Can it hold 500l of water?
∫0p C(x)dx = ∫0p [2500x0.5-70x]dx=
[(2500/1,5) x1.5 - 35x2]0p =
(2500/1,5) p1.5 - 35p2 - 0 = (2500/1,5) p1.5 - 35p2
This must be equal to 500l . We have that 1l=1000cm3. Thus 500l=500.000cm3.
Thus (2500/1,5) p1.5 - 35p2 = 500000
Thus p=49.9
Example 16:
Fig 3. The area defined by the boundaries x=a, x=b, and f(x) and g(x),
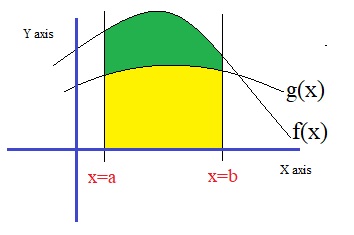
Often, at math Highschool exams, you may see tasks as the one listed below.
Suppose, over the domain [x-a, x=b] we have two functions f(x) and g(x).
Calculate the surface determined by the boundaries x=a, x=b, the x-axis, and which lies between
f(x) and g(x).
In this case, the question is about the size of the green area AGreen. See the figure above.
Thus:
AGreen = ∫ab f(x) dx - ∫ab g(x) dx
Note that we must always do "upper area - lower area".
Let's do a simple example. Say we have the line f(x)=4x+2, and the parabola g(x)=x2+2.
We do not have "a" and "b", so we must find the x value(s) of the intersection(s) first:
x2+2=4x+2 => x(x-4)=0 => x=0 or x=4.
The line is above the parabola, between x=0 and x=4, and for x>4, the parabola above the line.
The area we need to calculate, is thus in the interval 0<=x<=4.
We have ∫04 (4x+2) dx - ∫04 x2+2 dx =
[2x2 + 2x]04 - [1/33 + 2x]04 = 10.7.
Example 17: Calculating a Volume.
Imaging the function f(x)=√x. If you do not know how "the function looks like",
then look it up.
Now, imaging that we rotate the graph along the x-axis, over 2π. A tree dimensional object
is created, which looks like a 3D parabola, with the x-axis as it's center line.
If you would chop up the object over small Δx, we get small objects looking like small cilinders.
The volume of such small cilinder, at a certain location xi, is approximated by
π (f(x))2 . Δxi (like "π r2 . h", for a cilinder with width "h").
If you would add all those small cilinders, in an interval [x=a, x=b], you obtain the Riemann sum
which is a close approximation for the total Volume over the interval [x=a, x=b].
Thus, a definite integral exists, if Δxi gets infinitsemal.
Suppose we want to calculate the Volume in [x=0, x=4], we have:
∫04 π(√x)2dx = 8 π
-------- dx
(1+x2)3
----------------
2x+1
----------------
2x+1
----
2x+1
----------------
2x+1
----
2x+1
-------- dx
2x
-------- dx
2x
--- dx
2x
--- dx
2x