I like to talk about the Redshift, a little while later.
It's often cited that a cluster contains from about 100 to a 1000 galaxies, but ofcourse many have
even more galaxies. Superclusters contain usually many tens of thousends, or more, galaxies.
It is indeed true that the Galaxies in a cluster, are bound by Gravity. Today, there are good grounds
to say that the mass contribution from the galaxies themselves, to the total mass, is very low!
Generally, there is a consensus among astronomers that it's only a few percent. Then there is a contribution
due to "Intergalactic gas" (maybe up to 10%). But the very larger part comes from Dark Matter.
It's really amazing how many astronomers think of the total mass today, and that most of it is attributed
to Dark Matter.
Already in the early '30's of the former century, Zwicky found that the velocities of outer galaxies
in the Coma galaxy cluster, was way, way higher than could have been expected from the Mass of the Cluster
based on observable matter. He already at that time suspected a large contribution to the total mass due
to "dark matter" or "unobservable matter".
In his view, the Cluster would simply dissolve, simply because the galaxies would escape. It was just
a matter of time. So, "something" ties the observable matter (normal matter) together.
Indeed, Dark Matter is almost "unavoidable" in modern theories on Clusters. If it turns out that
it does nor exist afterall, an alternative explanation for the existence of clusters must be found.
1.2 Relative Positions of the Milky way, the Local Group, and the Virgo Cluster.
You see? A cluster is somewhat of a special thing, actually. But the Milky way, our own Spiral Galaxy,is that not part of a Cluster? This is a very good question !
First, the Milky way is part of the "Local Group", containing about 50 galaxies, where the Milky way,
M31, and M33, are the largest objects (spiral galaxies). Then, there are quite a few smaller dwarf galaxies.
The "Local group", is a "Galaxy Group", not so far from the edge of the Virgo Cluster.
Many folks say that the Local Group, span about 5 Million ly (Mly) or so, but some folks say its about 3Mly
while others go to about 10Mly. Anyway, as long as the Milky way, Andromeda (M31) and the Pinwheel (M33), and
about 50 or so dwarfsystems are in it, then it's OK I guess.
So, if someone would say that our galaxy is not really in a Cluster, I would not argue against it.
It's actually (relatively) near Virgo, but not really in it. It's near the rim of Virgo.
The figure below, explains it better. So, the Milky way is in a "Galaxy Group" (the Local Group), but
a bit outside the Virgo cluster.
Actually, if you would say "The Milky Way is not in the Virgo Cluster at all..", then you are
right. But as you will see below, our Milky way (and clusters and groups) are part of the Virgo supercluster.
Link to Figure 2.
Atlas of the Universe: neighborhood of the Local Group.
Figure 2, is much like a "zoomed in" part of figure 1. The Virgo cluster is about 65 million ly away from our
Milky way. Actually, what the whole of figure 2 shows, is The Virgo Supercluster, which contains the Virgo Cluster itself,
and the Local Group, and a number of other clusters like the Fornax cluster, the Eridanus cluster, and some dispersed
(smaller) Galaxy groups in that region.
We should now have a reasonable idea of "our Local neighborhood" on a Galactic scale.
1.3 Clusters as X-ray sources:
Typically, Clusters are X-ray sources, due to "hot" (but low density) "intergalactic intracluster medium (ICM)".This means that between the ordinary galaxy members, an intracluster medium (gas) exists, which is heated
to very high temperatures, thereby emitting X-ray radiation (interpreted as "bremstrahlung").
Although I said "low density", in comparison to intergalactic gas in our Local Group, the density is significantly
higher in Clusters.
Surveys using X-ray spectroscopy, like the ROSAT All-Sky Survey, clearly show that commonly the observable Clusters,
correspond to X-ray sources. X-ray spectroscopy can be used to further analyze the structure of Clusters.
It's even generally true that the Xray image displays the cluster as "one connected entity", That is, the full X-ray image
corresponds to the optical image.
This is a relevant difference between typical Clusters, and a typical "loose" Galaxy Group.
It's even true, that remote Clusters have been identified, initially by detecting the corresponding X-ray source.
It's still debated how the rather massive ICM originated, now to exist "inside" the cluster.
2. A few core concepts from Cosmology.
It's impossible to say something meaningful about Cosmology, in a simple note, of just a few pages.However, I just need a subset of elementary ideas from the whole of the Subject, so, let's see where I run off the clifs..
Below is a small potpourri of subjects, which I need for the Big Picture....
Note:
If you are young, it's good to say you should study Physics, or (probably) even better, Astronomy/Cosmology.
Ofcourse, you can later also choose to work at a silly Bank, or other silly financial institution, or silly government,
or something, and do boring stuff all day long, every "never-ending" day the same uttterly dull stuff.
Or..., you can study Astronomy/Cosmology, and discover the "why's" and "how's" !!!!
(ofcourse, something like Geology, Biology, or wild-life preservation, would be awsome too...)
2.1 Density parameter of the Universe:
It seems rather logical, that if the "density" of mass/energy is high, that the Universe might be positively curved,and that it possibly would shrink and collapse in due time. On the other hand, if the "density" of mass/energy is low,
the Universe might expand forever, and "gravity" cannot catch up (to let it collapse again).
The "critical density" ρcrit is exactly that bordervalue "in between" (so below it, would cause
the Universe to expand forever). Ofcourse, it has a certain value.
Historically, it was used to determine if the Universe is positively curved (slow down, plus collapse), or
negatively curved (expanding forever), or the Universe is flat, exactly at that bordervalue of ρcrit.
If we want to calculate the average "density" of mass/energy in our Universe, we need to consider:
(1): In our Universe, we ofcourse have Baryonic matter, by which we mean the ordinary particles like protons (or actually
the constituents, namely quarks) and leptons (like electron).
Maybe fermions was a better term (?), but everyone uses "baryonic matter".
(2): Secondly, it's strongly suspected that we also have "dark matter" (not the ordinary matter we all know of).
Dark Matter seems to interact only by Gravity. It's fully transparant for ElectroMagnetism, so, there is
not interaction with light, and other electromagnetic radiation, and is thus fully invisible.
(3): We also have radiation (photons) which represents mass/energy, so we must take that in account too.
Indeed, also stuff like neutrino's must be counted along.
We call that the "effective mass" from relativistic particles (photons, neutrino's).
(4): Now something strange: Dark Energy. Since 1998, this entity recieved an intense renewed attention. Indeed, it was
discovered that the Universe not only "expands", but it undergoes an "accelerated expansion", where the mechanics of it
is called "Dark Energy".
What is it? Countless physicists/astronomers/cosmologists, are breaking their brains on it.
Simply put: it's not certain yet. A good candidate seems to be Λ, which is the Cosmological Constant.
Einstein placed it in his equations, to make sure that the Universe would not collapse, since the consensus
at that time, was that we had a stable Universe.
It should work, sort of, as "repulsive gravity" to make sure that it counteracts the possible collapse,
due to "normal Gravity".
But since 1998, it was reckognized as a good "candidate" for the driving power behind the "accelerated expansion".
Note the difference between expansion, and accelerated expansion.
Yes, it all is not easy, but it's not easy for everyone...!
Now, we can add it all up, to arrive at the average density ρ. But it's better to scale it with the critical density,
that is ρ / ρcrit (and call that Ω), to see how far it deviates from "1" (>1 or <1).
That is:
Ω = ρ / ρcrit = Ωdensity due to (Baryonic + Dark Matter) + Ωdensity due to Radiation + Ωdensity due to Λ
Amazingly, the calculation shows that it is close to "1".There are several methods to figure it out. The CMB data of WMAP or (the later) Planck data has been used too.
Don't ask me now how they did that (sort of angular distances), because I will tell that slightly later.
The results are:
-Ω(Baryonic + Dark Matter) = 0.27%, where Baryonic matter only constitutes 0.044%.
Thus the "Matter" contribution is about 0,27%, and most of that is due to Dark matter.
-ΩRadiation = (about) 8.2 x 10-5. This is a very small contribution.
-ΩΛ = (about) 0.73%.
I am not amazed, if you would be amazed by that.
Slightly better calculations give: 71.4% due to Dark Energy, 24% due to Dark matter, 4.6% due to Normal matter.
(if you look at various articles, you may find slightly different values. Don't be alarmed by that.)
If Ω indeed would be "1", then something is not right?
Well, if ρcrit > 1, then it would be rather sound to say that the expansion slowly stops, and the Universe would contract,
probably into a Big Crunch.
If ρcrit < 1, then it would be rather sound to say that the expansion slows down, but goes on.
Now, what if Ω = 1? Then we are at the exact divisonline, between slowing down expansion and the followin collapse, and
that the Universe will go on with expanding. The only thing we then can say is that the Universe (SpaceTime) is flat,
with no curvature at all.
Now, we found Ω = ρ / ρcrit; to be "1" (with certain error margins).
Experimental data (since 1998), shows that we have an accelerated expansion. So, what is going on here?
Yes, We indeed need more information. Solely on the basis of section 2.1, we seem not to arrive at good conclusions.
But, the most important thing is, that you followed the reasoning, although we are puzzeled right now.
It is quite possible, that Clusters are not too much affected by the accelerated expansion. The relatively tight
object, in general, contains enough gravitational potential to slow down any expansion.
This too, is under study by nummerous astronomers. If it's indeed true, it might be interpreted as another
pointer for the existence (of higher amounts) of Dark Matter in Clusters, counteracting dispersion of galaxies.
Indeed, it seems that nowadays, consensus exists among astronomers, that at places which are strongly bound
by gravity (inside a Galaxy, a cluster of Galaxies), that this works "against" global expansion.
For this moment, global expansion seems to be valid only on larger scales, say over several millions of ly, outside
galaxies and clusters, because gravitational attraction, especially due to Dark Matter, seems to binds matter,
so that the global metric expansion is undetectable on smaller scales (like in a Cluster).
It's not confirmed, but it might even be so that the large voids between the filaments and walls, are thus
affected largely by the (dark energy driven) expansion.
Note:
Something is nagging me a bit. Dark Matter is not fully 100% proven. However, the majority of physicists accepts it.
But, before we explain everything, using Dark Matter, we must realize that it might be wrong.
I am not saying that it is wrong. But, some great thinkers in our time, are searching for alternative Gravity theories,
which possibly can do without Dark Matter.
Actually, I am not saying much substantially here, but only we need to be a tiny, very tiny bit careful, in taking a sort
of postulate for granted. Personally, I used think that there actually are too many pointers which make Dark Matter indeed a proven fact.
So, I was pretty much "pro", given the rather overwhelming amount of evidence.
Indeed, we can hardly do without Dark Matter anymore...
But I slowly start to loose faith in Dark Matter..., yes, me too. Unless it gets finally "found".
But who knows? Maybe an alternative pops up, or a better theory... Who knows..? Not very likely, as it seems presently,
but who knows? Large shifts in thinking are not uncommon in science.
- Maybe "primordial black holes" will replace the idea of Dark Matter (not so likely I think).
- An enhanced Gravity Theory then? (yes, as time moves on, I started to like the theory of Verlinde more and more).
Dark Matter is part of the Standard Model, notably the ΛCDM model. And for now, it's awfully difficult to explain the CMB analyses,
without Dark Matter (later more on that).
2.2 The Hubble parameter:
There is a one version ofcourse, but it's possible to wrap it up in a relatively easy description, anda bit more involved version.
Relatively easy approach:
In the early twenties of the former century, the Universe was considered to be "static".Slightly after the time when Einstein published his General Theory of Gravity, Friedmann gave a solution
for the "state" of the Universe, which can be interpreted as a Universe which expands.
The theory also uses a "scale factor" which directly relates to (or leads to) an expanding Universe.
Ofcourse, this all is related to the former chapter, but we will discuss this again in a while.
This section will discuss the Hubble parameter.
As of 1912 (Slipher), it was discovered that light from remote galaxies is redshifted. This suggested
as a sort of Doppler effect, meaning that those galaxies are fleeing away from us.
After important work of Friedmann and Lemaitre, Hubble did many observations, which finally led to
the famous Hubble Law (or Hubble-Lemaitre law):
v = H0 * D (Hubble's Law)
where "v" is the recession speed of such a Galaxy, H0 is Hubble's constant, and D is the distancebetween us and that remote Galaxy.
In present time H0 is probably in the order of 72 km s-1 Mpc -1,
meaning an additional 72 km/s (apparent) receding "velocity" per 3.26 million lightyears.
This relation is linear, so the further away that remote object is, the faster it seems to recede from us.
In the statement above, the observation is true, but the interpretation could be better.
Consensus among astronomers exist, that it is not that galaxies themselves which move through space, but that
it is space itself, which expands. In a manner of speaking, the galaxies drift along the Hubble Flow,
as many astronomers call this general (global) expansion.
As a result, light from remote objects like galaxies, is "redshifted", that is, the wavelenght of the radiation
will be increased. The higher the distance is, the larger this shift in wavelenght will become.
Although it looks as if everything is flying away from us, we are certainly not at the "center" of the Universe.
An observer 1 billion ly away from us, would see a similar Hubble shift.
Figure 1: illustration of redshift (increase in wavelength). Light gets more "reddish".
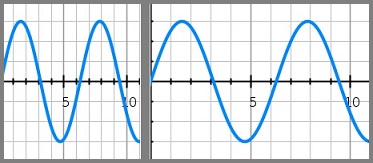
We already can try a simplyfied example of Hubble's law:
Example 1:
Suppose for a Galaxy it is found, that the recession speed "v" is 5*103 km/s.
Then: what is it's distance?
Using Hubble's law: 5000 (km/s) = 72 (km/s/Mpc) * D (Mpc)
So:
D = 5000 (km/s) / 72 (km/s/Mpc) => D = 69.4 Mpc = (about) 226.4 Million lightyears.
(1 pc = about 3.26 lightyear, 1Mpc = about 3.26 Million lightyears, 69.4 Mpc = 69.4 * 3.26 Million lightyears)
I can use this example, to state that the first true observable, is the redshift of light.
Thus this example is not how an astronomer would "start" to find "D",
Thanks to a relation of redshift and velocity, we thus can find the recession speed "v", and then we
have enough information to use Hubble's law to determine the distance "D".
Example 2:
As another example (not doing arithmetic this time, and just mentioning a fact): A galaxy of about 1 billion
lighyears away (109 ly), appears to recede from us with about 7% of the speed of light.
Can we already say something on the nature of the expansion of the Universe?
- Is "new" space created all the time? Likely not.
- Is space getting "streched" more and more? Likely not.
- Is it associated with the metric involved? Likely to be true.
The second option does not seem so strange, since an often used analogy of the expansion of the Universe,
is a balloon. If you draw some dots on the surface (representing galaxies) and you inflate the balloon,
then all dots are recede from each other.
This looks surprisingly as what seems to happen in the real Universe.
But the true mechanics behind it, is likely to be a time-dependent metric.
Although I personaly do not write off option 1. Because, since the start of the Inflationary period,
it's really so that Space is created (?), instead of a metric alteration... So, is inflation really over?
A little more involved approach:
Actually, it is pretty much sure that the Hubble constant "H", is time dependent.When we see the constant with a subscript, as in "H0", we mean that it is the Hubble value
as it is "today" (the present).
It is indeed true that current attempts to determine the value of the Hubble constant, deviate
considerably from determinations using CMB data. For example, current studies to remote objects
may give us typical values around 73.4 km/s/Mpc or even higher, while CMB data (from the first phases of
the Universe) may give a value of around 67.4 km/s/Mpc.
This is all reasonably close. When you compare that from values from the '30's up to (say) 1990,
then in these days the values obtained fluctuated many tens of km/s/Mpc.
Ofcourse, the question pops up: Is the Hubble constant really time dependent? And why?
Yes, it's likely time dependent. It seems that our Universe went through various phases of "Dominant stuff",
like in the very early phase, radiation dominance, then matter dominance, and now dark energy dominance.
Such a picture fits the expansion of the Universe quite well, counting from shortly after the Big Bang,
up to present times. Indeed, various degrees of expansion happened at those phases.
And now, we have an accelerated expansion, due to dark energy dominance.
Let's see what else we can do with the Hubble constant.
Let's see if we calculate the "inverse" of the Hubble constant (taken H0 as 72 km/s/Mpc):
| tH | = |
1 --- H0 |
= about 13.8 Billion years (13.8 * 109 years) |
Why? Look at this (if you do not like calculations, you do not need to follow the arithmetic below):
v=H0 * D. That is our basic Hubble Law.
Suppose we had a constant expansion since the Big Bang. Then we also have D = v * t => t = D/v thus:
t=d/v = d/(H0 * d) thus:
t=1/H0 (or tH=1/H0)
A good (*) value for H0 seems to be H0=72 km/s*Mpc, where 1 Mpc=(about) 3 * 1019km
Now, we have a time unit (s) in the relation above, so we can rework H0 to:
1/t = 72/(3*1019) = 24/10-19 => 1/t = 2.4 * 10-18
=> t = 1/2.4 * 10-18 = 4.2 * 1017 seconds.
Now, let's rework the number in seconds, to years:
=> t = 13.3 * 109 year.
So, using a reasonable value of the current Hubble constant, (taken H0 as 72 km/s/Mpc),
we arrive at t = 13.3 * 109 year. This is awfully close to the best calculated value of
13.8 * 109 years, which is the Age of the Universe.
I think it's safe to conclude that tH = 1/H0, corresponds to the Age of the Universe.
I am not saying that it exactly equates to the Age of the Universe. Do not forget that we also used
the idea of a constant expansion since the Big Bang, also evident in using D = v * t.
In the discussion, we also need to review what is behind the notions of "proper distance" and "comoving" distance.
That will be done in the next section.
It's true, that in some Local Group of galaxies, some galaxy might move towards some other galaxy.
That's certainly not uncommon. So, on smaller scales, blue shift due to motion towards the observer,
is quite common.
For example, the Andromeda Galaxy, M31, of a distance of about 2.2 - 2.6 million ly (which is relatively small),
moves towards our own Milky Way.
These motions, due to local gravity effects, are quite normal in a Group (or Cluster).
Hubble's law works for the "cosmological expansion". The smaller vectors (speed magnitude and direction) within
a Local Group of galaxies, do not count for the Hubble Flow, so to speak.
These (local) velocities are often called "Peculiar velocities". You might immediately say, that we should do
a velocity vector addition, of a (generally) larger velocity due to expansion, and a (generally) smaller
vector due to local movement in a Group. Sure, but Hubble deals with Cosmic expansion, where Space itself
expands, and the remote galaxies are simply in that flow.
This is an area where the notion of "comoving coordinates" may help, to understand these matters, better.
Thus: Hubble's law actually functions well on somewhat larger distances, thus where the Hubble flow is dominant.
Then we are really talking about the expansion of the Universe, and not about "local movements".
Also note, that in one example above, we used a Galaxy at a distance of a billion (109) lightyears, and
we found that the recession velocity (due to expansion) was 7% of the speed of light.
Any "local movement" of that Galaxy in some local group, is almost insignificant compared to 7% of the speed of light.
Note too that redshifts on larger distances are due to the expansion of Space, and is not really a Doppler effect.
Although many people say that it is (but it's not so terribly fundamental really, how one would call it).
The local movements within a group, which might lead to a redshift or blueshift of spectral light, is now
really due to relative velocities (not expansion), and this time it is more justified to call it the Doppler effect.
2.3 "Proper distance" and "comoving" distance: (1): A too simplistic approach!
In this section, there is a certain danger to talk in a circular fashion, or talk about objects which mighthave been gone already (or are beyond the "horizon").
=> For shorter distances (although we have not properly defined distances yet), like for the objects in the Local Group,
distances might be in the order of 5 million lightyears or so. This is pretty close, as you know.
There is not really a problem in saying that the Andromeda galaxy (M31), is about 2.2 million lightyears away.
Although the light from Andromeda we receive, was send out 2.2 million lightyears ago, at this time,
it has not moved dramatically further (or closer) to us.
All movements are due to gravity effects, and not noticable by cosmic expansion (for which the Hubble law applies).
For Galaxy Groups (like the Local Group), and inside clusters, then inside, the cosmic expansion is not "felt"
so much, due to the strong gravity bonds between the objects.
=> For larger distances, the cosmic expansion gets a grip. Very remote objects seem to fly away from us, and the further
they are, the faster they seem to go.
We know that the objects (like galaxies) do not move themselves, but it is in fact space itself which expands.
It's observed by the redshift of radiation emitted by those sources.
We know that in this case, the Hubble law does apply. As of (say) 100 Mpc (or about 300 Mly), Hubble's law works
pretty well.
Now, what is distance? Ofcourse we know what distance is, here on Earth, or in the Solar system etc..
But when it really is getting large, there are some extra considerations to do.
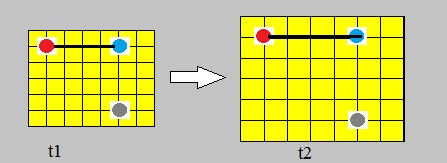
Comoving coordinates, Comoving distance "l", and Proper distance "L":
Figure 2: illustration of Comoving coordinates.
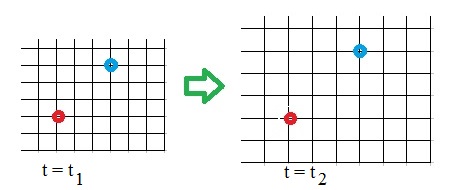
If we consider fundamental observers, in different Galaxies, then the Hubble flow would "preserve" the "pattern",
that is, we may think of them as tied on the grid (the coordinate system), and as space expands, so does
that coordinate system. However, the coordinates of the galaxies then does not change.
In figure 2, this is illustrated. Suppose in the left figure, at t=t1, the red system is in (0,0),
and the blue system in (3,3).
Now time passes, and space expands. The relative positions of those galaxies are still the same.
Thus at t=t2, the red system is in (0,0), and the blue system in (3,3).
This reasoning only holds, for rather large distances.
Comoving coordinates look like "rubber bands" between the galaxies, instead of rigid bands.
Note:
In many articles, it is said that the comoving distance between objects do not change, literally.
This is probably correct for relative small distances between objects. But for really larger distances,
it must change in time, otherwise you do not have expansion, or you would have a preference for direction.
And, you would not have any redshift (except for peculiar velocities).
What is often meant behind "distance between objects do not change" is that the relative postions
(in the comoving coordinate system) do not change, which is indeed true.
There are quite some opinions between authors, I have noticed. Some see this all equivalent to "scale factor expansion",
which seems correct to me. However, all in all, I would say that it's not an easy subject, and with some
If in this 2D analogy, the coordinates are know, we can easily calculate the distance "l".
Note, that at t=t1, and t=t2, the distance between both systems is still the same !
They do not "move" in this special "comoving coordinate system". But this whole system rescales with time.
But since (only) the scale of the coordinate system has changed, we also speak of a scale factor a(t).
Now you might say, that the real distance "L" has changed, otherwise it would be quite quirky.
Yes, that is true, the "real distance", or physical distance, or proper distance, might be written as:
L = a(t) * l (for shorter distance)
Note that a(t) indicates that the cosmic scale factor is a function of time, and its value thus changes with time.But what is the real distance? The comoving, proper, or geodesic? So, again, we must go deeper than this.
The further significance, and equation of a(t), will be discussed at the section of the Friedmann equations.
I must immediately say, that astronomers practically always talk about the redshift "z". We are going to see
this entity in the next section. So, for example "z=2" is rather far away, and "z=8.6" is almost at the Horizon.
Well, at least, the few astronomers I know, practically only talk about z, and only if the object is really quite close,
(say, couple of million ly, to a few hundreds of million ly), they use "ly" or parsec.
If a system shows a redshift of 9 (or thereabout), you might practically say that it is over 13 billion lightyears away.
It's very close to the Hubble Horizon. Furthermore, what can we say about the "current status" of such system?
It is over 13 billion years ago, that it send out that light, which we see now.
So what about it's status "now"? Such things are not easy to answer. That system might already have changed significantly,
or is now fully causally disconected, since it crossed our Horizon (later more on that).
How proper is the "Proper distance"?
I will repeat figure 2 again, but this time where the blue system send out a signal at t=t1.
We receive that signal at t=t2.
Figure 3: illustration of Comoving coordinates. The blue system at (3,3) sends a signal at t=t1. We receive that at t=t2.
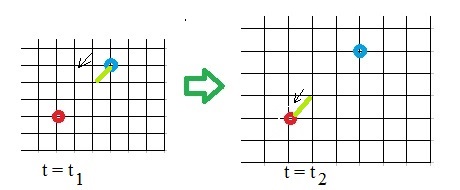
How about that? It looks like that the proper distance indeed is "one to one" to the physical, real distance.
There exists however, an interesting bug in this reasoning. And that relates primarily to "time".
There is another "bug" (so to speak), and that's related to "Ω.
So, the reasoning above is not correct, although for relative short distances it's a good approximation.
To understand this better, we also need to understand the "redshift", and, I'm afraid, review an enhanced "Ω" again.
Ofcourse, the 2D analogy depicted above, cannot model a Universe with a certain metric which has a certain curvature
depending on "Ω", and, which had a beginning (was "small") at about 13.8 billion years ago.
Suppose we wanted to calculate the real distance of a galaxy, say 6 billion ly away. Then there is a problem, since
we have observed the light, emitted 6 billion years ago (6 * 109). But then the Universe was much "smaller" !
It complicates the theory of large distances a bit. So, I will come back to this shortly.
The next section, I must say something substantial about the redshift.
2.4 Redshift "z":
Figure 4: illustration of redshift (longer wavelength) or blueshift (smaller wavelength).
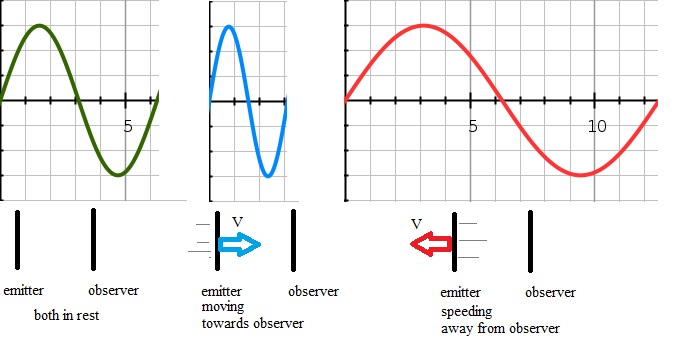
Change in wavelength of radiation, due to cosmic expansion, is not exactly the same, as the well-known
Doppler effect (due to relative velocities). But, the "effects" are quite comparable.
Note:
You: "Hey Albert. Don't be such a pain ***. Astronomers speak of a recession velocity, don't they?
So, it's Doppler !" Albert: "Uhhh.. Yes, that's a valid viewpoint, ofcourse. I only wanted to stress the wavelength change
due to expanded space. But observed, is redshift of spectra, related to recession velocity, due to expanded space.
Even Hubble's law shows this."
To illustrate the Doppler effect, imaging an emitter of sound waves, and you, the observer, and both are in rest.
Now suppose the emitter is moving towards you, with a considerable speed. Then, you hear a higher pitch.
In fact, the soundwaves are compressed, making the frequency larger and the wavelenght shorter.
Next, suppose the emitter is moving away from you, with a considerable speed. Then, you hear a lower pitch.
In fact, the soundwaves are stretched out, making the frequency lower and the wavelenght longer.
So, the Doppler effect has it's origin in relative velocities with respect to the observer and emitter.
However, here, we mean the readshift due to expansion of space. With respect to the observed effect, it
is completely similar to the Doppler redeshift. The idea is that in the laboratory, from a range of elements,
the spectra are known (related to the wavelength, or frequency).
Light from Remote objects then show a "shift" in those spectra, which has it's cause in the "additional" (in a
manner of speaking) space travelled. If it's about the cosmic expansion, it has to be a redshift, that is,
a shift to longer wavelengths.
If we would have an equation that relates the redshift to the receding velocity, or even better, directly to
the "distance", that would be fantastic ofcourse.
Some fundamental relations are:
c = λ * ν
where "c" is the (constant) speed of light, "λ" is the wavelength, and "ν" is the frequency.
This holds for any type of ElectroMagnetic radiation.
Note that if e.g. the frequency is high, then the wavelength is short, and vice versa.
| z | = |
λobserved - λemitted --------------- λemitted |
= |
λobserved --------- λemitted |
- 1 |
Above we see a completely logical relation. Ofcourse λobserved - λemitted is the difference
in wavelength, related to the travelled distance in expanded space. If we norm that against the emitted wavelength,
we have exactly in the "shift" in wavelength, or the "redshift".
(We may also write the above as: z + 1 = λobserved / λemitted).
Or even better: we know that the scale factor (see former section), a(t), works everywhere.
The scale factor ofcourse, simply must have a relation to the redshift.
Indeed, the relation found is:
| 1 + z | = |
a(tobserved) ----- a(temitted) |
Now, at the moment. we have a few relations of the redshift "z" to λ and a(t).
Can we show Hubble's law now, which relate the recession speed vr to the Distance?
Remember that Hubble's law is "vr = H0 * D".
Yes, we can do that, but you would immediately ask: Is it the proper distance? Is it the comoving distance?
Is it the Geodesic? If not, what sort of distance is this then? And at what time is it valid?
According to e.g. Peebles, Hogg, who are much involved in cosmic distances, the integration over time or z,
along the line of sight, represents the "best interpretation of distance". I will try to sketch that later.
This is why I want to derive Hubble at the end of section 2.5.
Hopefully, the goal of this section, namely a better understanding of "redshift", has been reached (a bit).
2.5 "Proper distance" and "comoving" distance: (2): A better approach!
Here, we will see (sort of) two parts:-The same theory as in section 2.3, but this time in accordance to general/classical large scale cosmography.
Thus, this will be more accurate.
-A description which is more in line with the model ("Ωtotal mass (baryonic + DM);", "ΩΛ") = (0.3,0.7).
Let's try to see how the latest CMB findings, might affect the above.
2.5.1 "Proper distance", "comoving" distance, Geodesic:
-"Proper distance" vs "comoving" distance:In section 2.3, we already have seen comoving coordinates. If we consider fundamental observers,
in different Galaxies, then the Hubble flow would "preserve" the "pattern",
that is, we may think of them as tied on the grid (the coordinate system), and as space expands, so does
that coordinate system. However, the coordinates of the galaxies then does not change.
It's meant to work where the cosmic expansion is in effect.
Let's call the comoving distance between Galaxies "s(t)". The expansion can be described by the scale factor "a(t)".
Ofcourse, when we consider two galaxies which are relatively remote from each other, s(t) will increase with time.
The "proper distance R(t) = comoving distance s(t)", at a certain time. This may sound strange
at first, but suppose you freeze the Universe at a certain precise moment. Then, you, in the Red Galaxy, measure
the distance to the Blue Galaxy. Then you find the proper distance. If you then Unfreeze the Universe, the scale factor
expands the grid again and the comoving distance grows again.
But at any frozen time (specific "t", or "present time"), we have "proper distance R(t) = comoving distance s(t)".
So, the proper distance, has a great name, but is not so proper after all. You must have an instaneous ruler
from your Galaxy, to the remote Galaxy, to determine the proper distance.
For most practical distance determinations, it seems that the comoving distance gives us more substance.
If you want to calculate the comoving distance ST from t=tA to t=tB, then we should calculate:
ST = |
∫t=At=B |
c * dt
|
(Hopefully, you can properly see the equation. Sorry, I am not such a tiger with HTML and stuff.
Probably, that shows.)
You could explain the equation like so: Ofcourse, "c" is the speed of light. Thus c * t is a distance.
A small distance, but more accurate, would be "c * Δt", where "Δt" is extremely small
If we divide the whole timepath into a large number of "Δt's", and add all corresponding "c * Δt" parts,
we get the integral (as denoted by the ∫ symbol).
But we must "norm" that against the scaling factor, which determines the expansion of space.
So, the parts we all add up, is actually "c * Δt / a(t)". When we take the limit of Δ,
we get the integral.
Using this reasoning, it would follow that the integral is a "reasonable" to find ST.
Ofcourse, a bit problematic would be a(t), since we do not know the exact function right now.
However, the equation above, is in a general format. To get a more realistic equation, you need
the metric which is in effect (or you think is in effect), and somehow you need to take Ω in account too.
-"Geodesic":
In General Relativity, a geodesic is the equivalent of "straight line" in (e.g.) 3D euclidean space.
That's not an explanation ofcourse.
Again, the metric you want to use is critical. The traditional one, a school example in Cosmology,
is the Friedmann-Lemaître-Robertson-Walker metric (FLRW), also called FLRW Cosmology.
FLRW is not "just" a metric. It's the foremost solution of Einstein's equations,
and it has enormous important place in Cosmology.
It's the shape of the path of a "free" particle, except for the influences of the constituents of Ω,
and this should be accounted for in the metric.
There are many examples of FLRW, for example, where folks study a Universe with radiation only, or a Universe
where Ω equals ("Ωtotal mass (baryonic + DM);", "ΩΛ") = (0.3,0.7).
When I say that Ω is accounted for in the metric, is when you see a parameter (often called κ ),
in the equations, and this parameter then determines the curvature of SpaceTime.