Basic arithmetic/calculus.
In the series: Note 14.
Subject: Surface and Volume Integrals or calculations.
Date : 3 July, 2016
Version: 0.3
By: Albert van der Sel
Doc. Number: Note 14.
For who: for beginners.
Remark: Please refresh the page to see any updates.
Status: Ready.
This note is especially for beginners.
Maybe you need to pick up "some" basic "mathematics" rather quickly.
So really..., my emphasis is on "rather quickly".
So, I am not sure of it, but I hope that this note can be of use.
Ofcourse, I hope you like my "style" and try the note anyway.
This note: Note 14: Surface and Volume Integrals or calculations.
Each note in this series, is build "on top" of the preceding ones.
Please be sure that you are on a "level" at least equivalent to the contents up to, and including, note 13.
This note is a very short introduction into "Surface and Volume Integrals or calculations".
Chapter 1. What are we going to do here?.
In this note, we are going to explore how to deal with, and how to interpret, integrals as shown below:
1. Functions as y=f(x) (see Chapter 2)
These are our well-known functions, as y=f(x), which can be graphed as some curve or line in the XY plane.
Here we might encounter definite integrals like:
∫ab f(x) dx = F(b) - F(a)
Where F(x) is the "primitive" function of f(x).
Please see note 8 for a discussion of the "primitive" function. However, here we largely repeat it again.
But if needed, please revisit note 8 again.
The interpretation of such "definite integral" (with boundaries "a" and "b"), is that it often can be identified as the
surface area between f(x) and the x-axis, in the interval a ≤ x ≤ b.
2. Functions as z=f(x,y) (see Chapter 3)
Functions as z=f(x,y), which often can graphed as some "surface" in XYZ space (R3).
Here we might encounter definite integrals like:
∫A f(x,y) dxdy
Where "A" often is some rectangle in the XY plane, for which hold that a ≤ x ≤ b and d ≤ y ≤ e.
Sometimes, such an integral is also notated as:
∬A f(x,y) dxdy
The integral can often be interpreted as the Volume enclosed by z=f(x,y) and the area A on the XY plane.
Note: The double integral symbol, then should indicate that we work over multiple dimensions.
3. Functions as w=f(x,y,z)
Functions as w=f(x,y,z), cannot be simply graphed anymore: the space defined by points (w,x,y,z) is 4 dimensional.
Here we might encounter definite integrals like:
∭V f(x,y,z) dxdydz
Where "V" *might" represent a "volume" bounded by certain conditions.
In this case, various interpretations may exist, just depending on what f(x,y,z) actually represents, e.g. density of some material
throughout the body of material, or the value of some scalar function in Space etc..
I don't think that I will go into integrals of f(x,y,z) in this note. I'am afraid the note would be too cluttered.
I will do that later, in one of my "basic physics notes".
I think, that for a basic series of math notes, it would be great if you could browse through chapters 2 and 3,
and get the "general picture" on how this stuff works.
Note on interpretations:
Also in (1) and (2) above, it is true that we cannot always interpret the result of the integral, as to be a surface (1) or volume (2).
But in most cases, and certainly in the math we see here, the interpretations are correct.
Chapter 2. Definite integrals of y=f(x).
Let's first recall what the indefinite Integral (or primitive function) is:
The In-definite Integral
Please recall from note 8, that f(x) might have a "primitive function F(x)", if it holds that
F '(x)=f(x)
So, f(x) is actually the derivative function of F(x).
Example:
Suppose f(x) = 4 x2
Then what is the primitive function F(x) of f(x)?
F(x)=4/3 x3 + c
This is so since F '(x) = 3 * 4/3 x3-1 = 4 x2
In general, the (in-definite) primitive function is written as:
∫ f(x) dx = F(x) (equation 1)
Definite Integral
This time, the boundaries "a" and "b" in the integral equation, play a role.
The "claim" is, that:
∫ab f(x) dx = F(b) - F(a) =
Area between f(x) and the x-axis, in the interval where a ≤ x ≤ b (equation 2)
I am going to make this "likely" in the next paragraph. However, I like to provide an illustrative example first.
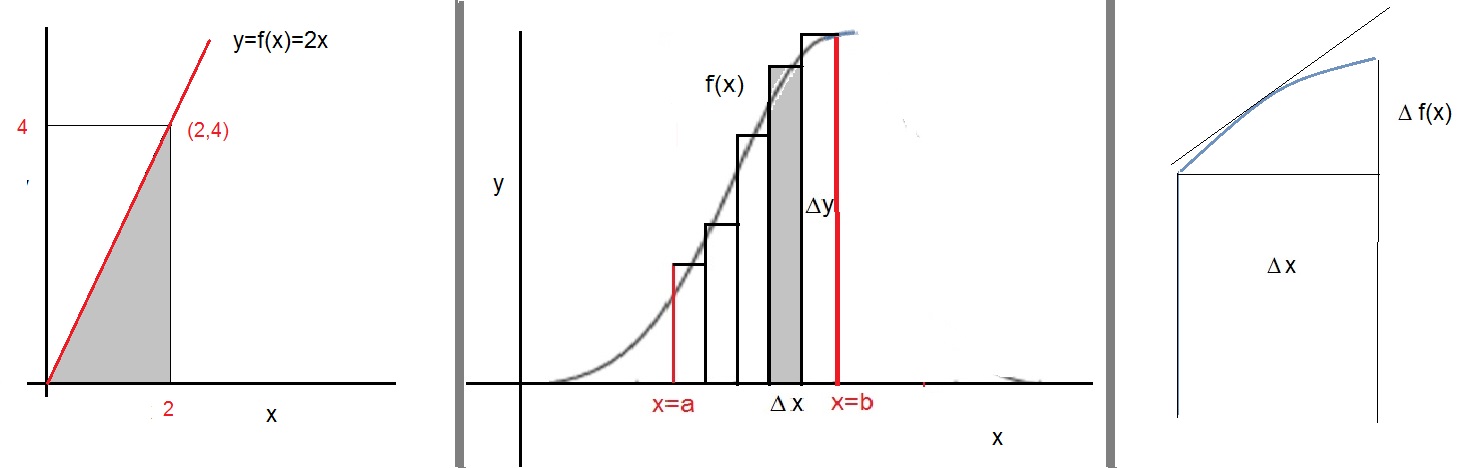
Suppose we have the line f(x)=2x. In figure 1, the left most picture illustrates the graph of y=2x.
This line goes through the Origin of the XY plane (0,0), and also goes through the point (2,4).
You can probably see that a right-angled triangle exist, defined by the three points (0,0), (2,0) and (2.4).
This triangle is just exactly half of the rectangle with sidelengths 2 and 4.
So, the total surface area of that rectangle is 8, and thus for the right-angled triangle the Surface area is 4.
Now, let calculate the integral. It should return the value 4 as well:
∫ 2x dx = x2
thus:
∫ab f(x) dx = F(b) - F(a) = F(2) - F(0) = 22 - 02 = 4
Indeed, the area is 4, just as we could see from the fact that the area of the right-angled triangle is exactly half
of the area of the rectangle defined by the points (0,0), (2,0), (0,4) and (2,4).
This reasoning will always work with linear equations of the form y=ax+b
Figure 1. Some illustrations that help interpreting a definite integral.
Optional reading:
If you would say: "If it works with lineair equations, that is, that the definite Integral is the same as the surface area
between f(x), the lines x=a and x=b, and the x-axis... then I believe the general case as well...
If that would be so, the rest of chapter 2 is optional reading. But you might give it a try.
Now, let's try to make equation 1 "plausible" for (continuous) functions in general.
Take a look at the middle picture in figure 1. Here, f(x) represents any continuous function in the interval a ≤ x ≤ b .
Suppose that you would not have any clue as to calculate the area under f(x) and the x-axis.
Then you can always "divide" that area into thin rectangulars, as illustrated in figure 1.
Next, you can easily calculate the area of any rectangle, since it's simply "length x width".
Suppose you would use 10 of such rectangulars. You can calculate the area of all ten of them, and next sum them all up.
It would be a nice approximation.
The more you would use, the more accurate you get. Let's denote the number of rectangles by "n".
Note that the width (along x) of such rectangle can be denoted by Δx, and the length by Δy.
For each individual rectangle, say number "i", we can then say that the width is Δxi, and it's lenght is Δyi.
The area of f(x) to the x-axis in the interval a ≤ x ≤ b then can be approximated with:
approximation of the area = Σ i=1i=n Δxi Δyi (equation 3)
Note: Σ is a shortcut for "summation", that is, that we sum all Δxi Δyi for all i from 1 to n.
Actually, I should not have used Δyi in above equation, unless we understand how to interpret it.
Although, from figure 1 above, it's OK to use Δyi, it's a bit better to use f(Δxi).
The "narrower" the rectangles become, the more accurate it is to use f(Δxi) instead of Δyi.
When "i" get's very large, such equations like equation 2, will get very accurate. In the limit, when "Δxi -> 0", then people
also call equation 2, a "Riemann" sum.
In the equation above, I used Δyi. Ofcourse, that is suggested by figure 1.
However, if Δxi is very small, then the corresponding y values are ofcourse f(Δxi).
Not exactly, but very close. If Δxi is extremely small, then it's very very close to being exact.
Just remeber that, as always, we have y=f(x). So, that's also true for a certain xi in the small interval Δxi
So, then we get:
approximation of the area = Σ i=1i=n Δxi f(Δxi) (equation 4)
Whether you believe it or not, an "definite integral notation" (thus with boundaries "a" and "b") is just another way to represent
a Riemann sum. It's just a matter on how you write things down. Thus:
∫ab f(x) dx = lim Δx ->0 Σ i=1i=n Δx f(Δx) (equation 5)
(In equation 5, I left out the "i" subscripts).
Since ΔF(x) = f(x) Δx (remember that in the limit it is true that dF(x)/d(x) = f(x), thus dF(x)=f(x)dx), we can write:
∫ab f(x) dx = lim Δx ->0 Σ i=1i=n ΔF(x) (equation 6)
But, suppose F(x) is a climbing function for x in [a.b]. Then summing Σ ΔF(x) over the interval x=a to x=b,
is really the same as F(b) - F(a).
Thus:
Surface Area = ∫ab f(x) dx = F(b) - F(a) (equation 7)
A few examples on calculating the area:
=> Example 1:
-Calculate:
∫02 (x2 + 1) dx
-Solution:
Since F(x)= 1/3 x3 + x + c (where c is any constant),
the calculation will be: F(2) - F(0) = (1/3 23 + 2 + c) - (1/3 03 + 0 + c) = 1/3 * 8 + 2 + c - c = (about) 4.6
Note that with definite intergral calculations, any "c" will have no bearing whatsoever, since it will cancel out.
=> Example 2:
This example may have a surprise for you. Let's calculate the area enclosed by sin(x) on the interval [0,2π]
-Calculate:
∫02π sin(x) dx
-Solution:
We know that if f(x)=sin(x), then the primitive function is F(x)=cos(x).
Thus:
F(2π) - F(0) = 1 - 1 = 0.
This is a surprising result. If you look at a graph of sin(x) in the interval [0,2π], then there is
definitely an area enclosed by sin(x) and the x-axis. However, at x=π, the function changes sign, and
the y values are negative. Please take a look at note 4, figure 4. Here it can be seen, that the area left
of x=π is equal in size to the area right of x=π.
You might say: the "positive" area, and the "negative" area, precisely "cancel" each other out.
That would not be the best interpretation. Most folks would argue that both area's should be added.
However, mathematically, in this example, the total integral just simply returns "0".
This is why a definite integral is often calculated over an interval, where the function does not flip it's sign.
So, if a function does changes it's sign at x=b somewhere in the interval [a,c], most people "split" the integral
in two parts, namely [a,b] and [b,c], and simply add the results.
It's not really strange, since it's a matter of interpretation too. Most people would do a split,
in order to obtain positive area's. But mathematically, you can integrate over an entire interval.
=> Example 3:
-Calculate:
∫02 1/(1+x) dx
-Solution:
First note, that the function "1/(1+x)" exibits asymptotic behaviour when x->-1, since when x=-1,
the denominator would be "0".
You can ofcourse calculate integrals, but not very close to "x=-1".
These sort of functions, using fractional components, might seem somewhat impressive at first sight.
In reality, when people use math a lot, they often "reckognize" classes of functions, and their primitives,
just by experience.
But here, we too are not defenseless. In note 7, we explored the "ex" and "ln(x)" functions.
There we saw that the derivative function of "ln(x)" is "1/x". So, here it is the other way around.
If needed, please see note 7 again.
Thus:
∫02 1/(1+x) dx = ln(1+2) - ln(1+0) = ln(3) - ln(1) = 3
Now, let's go to integrals of z=f(x,y).
Chapter 3. Definite integrals of z=f(x,y).
Take a look at figure 2. Here, you see a certain f(x,y), represented by the surface in R3.
Figure 2. A surface, as the representation z=f(x,y) in XYZ space.
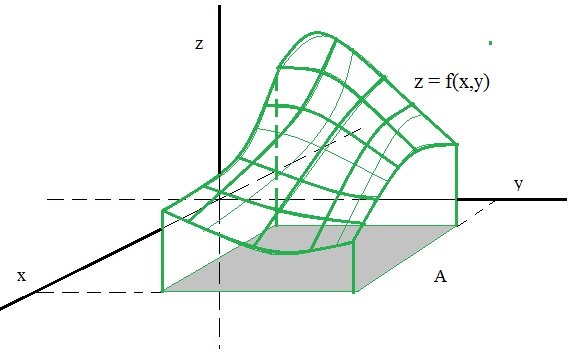
I'am not much of an artist, so I just hope you indeed see a "surface" in figure 2.
In figure 2, you see the square region "A" which lies in the XY plane. This is the region over which we integrate.
By the way, it does not have to be a square, or rectangular shaped.
If we integrate "over" "A", the definite integral is equal to the volume under the surface z=f(x,y).
Depending on certain circumstances, different interpretations exist, so a double integral must not always (!)
be interpreted as a "volume calculation". But often, it is indeed correct.
In analogy of chapter 1, we can divide the volume in small 3D blocks, starting on "A" and rising up to z=f(x,y).
You can always do an approximate Volume calculation, by using, say a count of 10 blocks along x, and 10 along y,
making a total of 100 rectangular blocks. The volume of each block is ofcourse "length x width x height", and you get
your approximation by summing all individual volumes to a grant total.
Or, you could use "n" blocks along the x direction, and "m" along the y direction, to make it more "general".
Algolrithm to approximate the Volume, if "A" is rectangular:
- you would take n=1 (along x), and then sum all volumes of the m blocks along the y direction,
- then you would take n=2 (along x), and then sum all volumes of the m blocks along the y direction,
- ...
- ...
- at last, you would take n=n, and then sum all volumes of the m blocks along the y direction.
Then, sum over all "n". Do you already see a double Riemann summation appear?
So, the approximation of the volume then would be:
approximation of the Volume = Σ i=1i=n Σ j=1j=m Δxi Δyj f(Δxi,Δyj) (equation 8)
Suppose area "A" is really rectangular. The corners then can be notated as "a" and "b" (along x) and "c" and "d" (along y).
If the blocks get very narrow, or in other words, n and m are very large, then we have a Riemann sum again.
Another way to denote the Riemann sum is using the integral notation:
∬Area f(x,y) dxdy = lim Δxi Δyj Σ Σ Δxi Δxi f(Δxi,Δyj) (equation 9)
Whether you believe it or not, in the "limit", the "definite integral notation" here, is just another way to represent
a Riemann sum again. It's just a matter of a universal agreement among folks, on how you write things down. That's all really.
Just as the algolrithm above, we would calculate the double integral, by integrating "over x" first, considering y as constant.
Then we would integrate "over y".
Or, if the math seems to be easier, we can integrate "over y" first, and then "over x".
In this way, you have a sort of "inner integral" you do first, en then you go for the "outer" integral.
I would not like to give you the impression that it always goes like this, because that would not be true.
But, in many cases, it does, so that's why you see it here as listed as the main method to solve integrals of this type.
To appreciate all this, you need to see an example:
Example:
Suppose we have the function z=f(x,y)=x2y.
It's a relatively simple function, but the "principle" applies to general functions as well.
We want to get the volumw of f(x,y), when the area "A" in the XY plane is characterized by:
A is the rectangle for which hold: 0 ≤ x ≤ 1 And 0 ≤ y ≤ 1
So, we have:
∬A x2y dxdy
∫01 ∫01 x2y dxdy
We can integrate "over" y first, treating x as constant. So, our "inner" integral then is:
∫01 x2y dy
= x2 ½ y2 │y=0y=1
=(x2 ½) - (0)
We are now left with the integral:
∫01 ½ x2 dx
This works out as:
1/2 * 1/3 x3 │x=0x=1
= (1/6 * 1) - (0) = 1/6
That's it ! Hope you liked it.

