Basic arithmetic/calculus.
In the series: Note 20.

Subject: Geometry

Date : 2 Februari, 2020
Version: 0.3
By: Albert van der Sel
Doc. Number: Note 20.
For who: for beginners.
Remark: Please refresh the page to see any updates.
Status: Ready. But subjects will be added in time.

This note is especially for beginners.

Maybe you need to pick up "some" basic "mathematics" rather quickly.
So really..., my emphasis is on "rather quickly".

So, I am not sure of it, but I hope that this note can be of use.
Ofcourse, I hope you like my "style" and try the note anyway.

This note: Note 20: The facinating world of Geometry.

Each note in this series, is build "on top" of the preceding ones.
Please be sure that you are on a "level" at least equivalent to the contents up to, and including, note 19.

-It's especially useful having knowledge about the goniometric functions (sin, cos, tan).
For example: see Note 4, completely.
-And, it's very important to have a good idea about vectors.
For example: see Note 12, up to section 2.1.

If so, then you are ready for this note !

I will not follow a crisp and clear "outline" here, but instead will "hop" from important topics in Geometry.

Chapter 1: Lines in vector representation.

1.1 Vector representation of a line in 2 Dimensional space (R²)

Especially from "calculus" (or "analysis"), we know how to represent a line in a 2 dimensional
(orthogonal) coordinate system (using an x- and y axis). Such a line can be written as "y = ax + b".

However, from "vector analysis", we know how we can represent vectors in some space (like a 2dimensional,
or 3dimensional space). If needed, study note 12 again (up to section 2.1 is quite enough).
Also, we know how to add two vectors, and we know of some other operations as well.
Take a look at figure 1 below:

Figure 1: two lines in R² in vector representation.

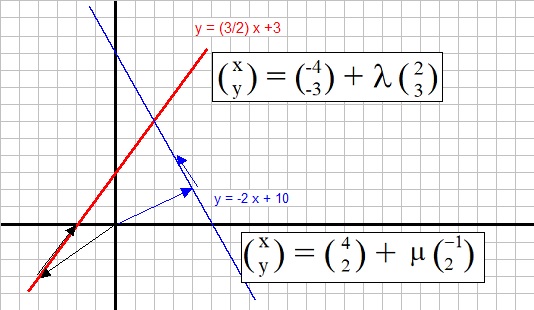
We see two lines, with the familiar notations "y = 3/2 x + 2" (the red one), and
"y = -2x + 10" (the blue one).

We can also represent the lines in vector notation. Let's try this for the red line:

┌ x ┐
└ y ┘

┌ -4 ┐
└ -3 ┘

┌ 2 ┐
└ 3 ┘

What a difference. No not really. The vector notation above, can be explained. It says: any point (x,y)
on this line "can be reached" by starting with vector (-4,-3) and, then adding the vector (2,3), where
λ defines the "amount" of which (2,3) must be multiplied.

So, for example the point (0,3) clearly is a point on the red line. To get there, from the Origin,
we can write it like so:

┌ 0 ┐
└ 3 ┘

┌ -4 ┐
└ -3 ┘

┌ 2 ┐
└ 3 ┘

Now, to reach any arbitrary point on the line, λ must take on specific values for those points.
So, for all points on the line, λ takes on values from the "real numbers" ℝ, like
for example 2, -2, 5, 100, 26.15, 19, 55290 etc... Only λ varies "per point".
Note that this is simply a matter of vector addition of 2 vectors.

So, indeed, this vector notation is able to fully describe this line, just like the counterpart
from calculus does (y=ax+b).

Note: the first vector is often called "position vector", and the second (in the direction of the line),
is often called the "direction vector".

A similar vector notation is ofcourse possible for the blue line. See below:

┌ x ┐
└ y ┘

┌ 4 ┐
└ 2 ┘

┌ -1┐
└ 2 ┘

Task: Try to verify that this notation is correct, using figure 1.

Here, ofcourse the number μ has a similar purpose as λ.

1.2 Vector representation of a line in 3 Dimensional space (R³)

Here, we have not really a fundamental change with respect to section 1.1 The only difference is,
that we now have one additional spatial dimension.
Take a look at figure 2 below:

Figure 2: A line in R³, in vector representation.

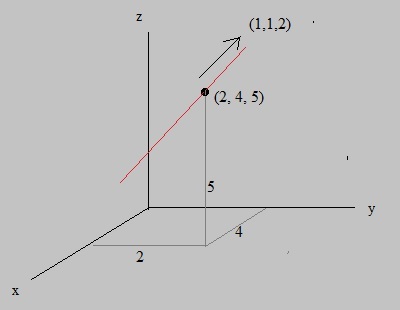
An example of a line in 3Dim space, in vector representation, is:

┌ x ┐
│ y │
└ z ┘

┌ 2 ┐
│ 4 │
└ 5 ┘

┌ 1 ┐
│ 1 │
└ 2 ┘

1.3 Intersection of 2 lines in 2 Dimensional space (R²)

Let's use the same lines again as we used in section 1.1. See figure 1 above. Suppose we want to find
the point of intersection of the two lines:

y = 3/2 x + 3 (the red one)
y = -2x + 10 (the blue one)

Obviously, where the lines intersect, the "y" (and "x") of both lines are the same.
So, we must solve:

3/2 x + 3 = -2x + 10 =>

3x + 6 = -4x + 20 =>

7x = 14 =>

x = 2.

We can find the corresponding "y" by using either one of the equations, and substitute "x=2".
Then we will find "y=6". So the point where both lines intersect is (2,6).
We have seen this theory before in "note 2: Linear Equations".

Now, we will do the same, but this time with the vector representations:

┌ x ┐
└ y ┘

┌ -4 ┐
└ -3 ┘

┌ 2 ┐
└ 3 ┘

┌ x ┐
└ y ┘

┌ 4 ┐
└ 2 ┘

┌ -1┐
└ 2 ┘

At the intersection, the "x" and "y" at that point must be the same for both lines.
Thus we have:

-4 + 2λ = 4 - μ (equation 1)
-3 + 3λ = 2 + 2μ (equation 2)

This is a set of two equations with two variables. We can solve it in the following way:
I want to isolate either λ or μ. I can do it like so: Multiply equation 1 by "2", and then add both equations:

-8 + 4λ = 8 - 2μ
-3 + 3λ = 2 + 2μ
---------------------------
-11 + 7λ = 10

-11 + 7λ = 10 =>

λ = 3.

Now, I may use the vector equation:

┌ x ┐
└ y ┘

┌ -4 ┐
└ -3 ┘

3 *

┌ 2 ┐
└ 3 ┘

┌ -4 ┐
└ -3 ┘

┌ 6 ┐
└ 9 ┘

┌ 2 ┐
└ 6 ┘

This is indeed the vector (from Origin) pointing to (2,6). So, we have found the point of intersection
of both lines. Note that the traditional representation (2,6), and the "vector", are equivalent in this context.

1.4 The perpendicular vector, to some vector.

From note 12, you may recall that, if we have two vectors A and B, then they are perpendicular
if the inner product A . B = 0. If needed, visit note 12 again.

The inner product is just a number (a scalar), and in case the vectors are not perpendicular, then
the inner product produces a number NOT equal to "0".
For vectors in R², the inner product is defined as:

A =	┌ a ┐ └ b ┘

B =	┌ c ┐ └ d ┘

Then A.B = a*c + b*d

Example:

Let A and B the vectors:

A =	┌ 1 ┐ └ 2 ┘

B =	┌ 3 ┐ └ -2┘

Then A.B = 1*3 + 2*-2 = -1

But if two vectors are perpendicular, the inner product is "0".

Thus: suppose we have the vector "A":

A =	┌ 1 ┐ └ 2 ┘

Now we want to find the vector A^P which is perpendicular. By drawing the vector above in the XY coordinate system,
we may quickly "guess" that the perpendicular vector is:

A^P =

┌ -2┐
└ 1 ┘

Let's check that. We calculate the inner product as: 1*-2 + 2*1 = -2+2 = 0.
So, we have indeed found the vector which is perpendicular.

Indeed. If we have:

A =	┌ a ┐ └ b ┘

Then the following vector is perpendicular.

B =	┌ -b┐ └ a ┘

Also, we see that in this case a*-b + b*a = 0.

One application is the following. If you have the vector representation of a certain line,
then you ofcourse have the "direction vector" in that representation too.

Now, you can immediately find the "direction vector" which is perpendicular. Just apply the theory above.
So, now you are almost done in finding the equation of the line which is perpendicular to the first line.

All you need now, is just finding (or locating) some point (which can be any point), which
lies on that second line. If you have that too, you can easily write down the vector representation
of that perpendicular line.

Chapter 2: Representation of a flat surface in 3 Dimensional space (R³).

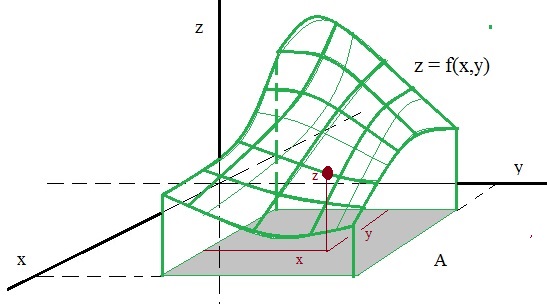
Usually, a function z=f(x,y) in R³, can be interpreted as a Surface in R³.
I say "usually", since that is not always the case.

If it's a function, then the points x, y in the plane defined by the x-axis and y-axis,
are mapped to "z values".
A simple example can be seen in figure 3, below.

Figure 3: An example function z=f(x,y) (green surface).

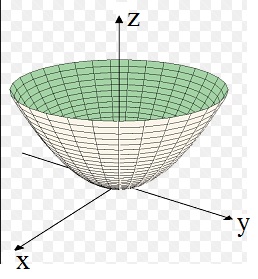
The next figure shows a 3D parabola surface, defined by z=f(x,y)=x²+y².

Figure 4: The function z=x²+y².

What about a flat surface? Again, just as we had with a line, we can use an approach from "calculus/analysis",
or we can try to formulate a vector representation of the plane in R³.

The Calculus/Analysis way:

If you look at the formula for a line in R², then it is the familiar formula "y=ax + b".
Maybe you will not be too much surprised to see that the relation for a plane in R³, can be written as:

z = ux + vy + h (u,v,h are some constant numbers)

However, usually the relation is rewritten (in generalized form) as:

ax + by + cz = d (a, b, c, d are some constant numbers)

Maybe you find the upper two equations plausible. There are only linear terms (no quadratic or other powers),
which strongly suggests that "z" varies linearly with x and y. Should be a plane indeed.

If you look at "z = ux + vy + h", and the numbers u and v are both zero, we have "z=h", which is a plane parallel
to the XY plane in the coordinate system.

A vector representation of a plane in R³:

It looks a bit like an "extended" vector representation of a line. You may ask yourself, which vectors do you need
to "reach" any arbitrary point in that plane.

Figure 5: A plane in R³, and how you can access any point in that plane.

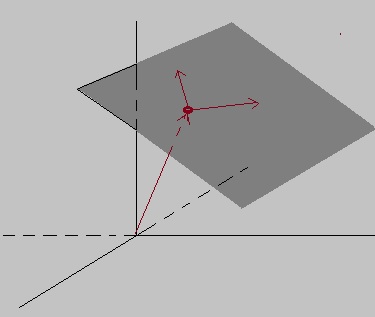
You need one "support vector" from the Origin, to any arbitrary point in that plane.
Next, you need two independent direction vectors, which reside in that plane. That way, using vector addition,
you can reach (or describe) any point in that plane.

The vector representation below is an example. The first vector is a vector from the origin to some point
in that plane. Then, we have two direction vectors in the plane. The factors λ and μ determine
how those direction vectors vary in "size", in order to reach any specific point in that plane.
In other words: specific values for λ and λ, determine a specific point in the plane.

Note that you can take any two independent direction vectors in the plane. So, the example below,
is just one of the infinite possible representations. However, it allows to describe any point on that specific plane.

┌ x ┐
│ y │
└ z ┘

┌ 2 ┐
│ 3 │
└ 2 ┘

┌ 1 ┐
│ -1│
└ 3 ┘

┌ -1┐
│ 3 │
└ 2 ┘

Chapter 3: Some further applications of the Pythagorean theorem.

We all know the Pythagorean theorem ofcourse. In a right triangle, where one angle is 90 degrees,
we have the relation that the square of the hypotenuse "c", is equal to the sum of the squares
of the other 2 sides.

Figure 6: A right angled triangle and the Pythagorean theorem.

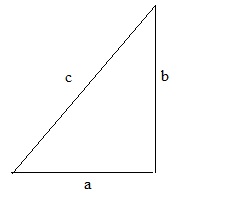
The relation is: c² = a² + b²

Suppose a=3, b=4, then we can calculate c² = 3² + 4² = 9 + 16 = 25. Thus c = √25 = 5.

You can also use the theorem, if for example "c" and "a" are known, and you want to calculate "b".

The upper is rather basic, ofcourse.

Some further applications:

3.1 Application in 3D objects:

Actually, there is nothing "new" here. I just want to make sure that you see the application of the Theorem on a 3D object.

Example 1:

Suppose we have a beam as shown in figure 7.

Figure 7: Application of the Pythagorean theorem in a 3D object.

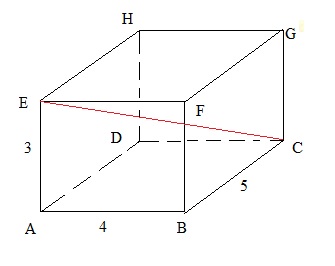
Can you calculate the length of EC (the red line)?

Solution:

You cannot immediately apply the Pythagorean theorem. But if we calculate the length of AC first,
then a triangle can be seen where EC is the hypotenuse, and ten the other two sides (EA, AC) are known.

So:

AC² = AB²+BC² = 4²+5² = 16+25=41

Thus AC= √41.

Now we have the triangle ACE, where AC and AE have known values (√41, 4).

Thus EC² = AC²+AE² = 41 + 9 = 50 => EC=√50.

We have our answer. But do you notice the remarkable fact that:

EC² = AE²+AB²+BC² <=> 50 = 3²+4²+5²

So, the square of such a diagonal in a beam is always the sum of the squares of the sides.
You do not need to memorize that. The important thing here, is that you indeed realized that you
needed to calculate AC first. Then the rest follows automatically.

Example 2:

We have the same beam again, as in example 1.
Figure 8:

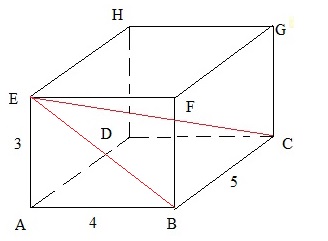
Are you able to calculate the ∠ BEC (the angle between the lines BE and EC)?

I hope you can remember the expressions voor sin, cos, and tan in a right angled triangle.
If not, please see note 4.

Solution:

There are multiple ways here.
Note that EBC is a triangle. One angle is 90 degrees. Which one? It's ∠ EBC.

I can calculate the length of EB first. Can you confirm that EB = 5?

Next, I can use the tan function.

tan(∠ BEC) = BC/EB = 5/5 = 1.

So, now I have "tan(certain angle)=1". That's great, but I want to find the angle.
For this we can use the "inverse" function of tan, namely notated as "arctan()" or "tan^-1".

You know how a function, and it's inverse work? If "f" and "g" are each others inverse, then f(g(x))=g(f(x))=x.

For example, f(x)=x² and g(x)=√x. Then f(g(x)) = (√x)² = x again!

Thus:

tan^-1( tan(∠ BEC) ) = tan^-1(1)

∠ BEC = tan^-1(1)
= (about) 0.78 rad = 45 degrees.

Don't worry. We will see many more angle calculations, with better explanation.

Example 3:

Take a look at figure 9 below. For now, concentrate on (sub)Figure 1.
If someone would ask you to calculate the length of PQ, you might think that this is quite some task.

Figure 9:

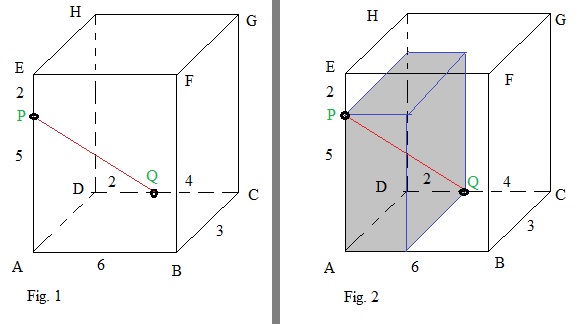
However..., you see what I did in (sub)Figure 2? I drew a "sub beam" inside the "main beam", and
the points P and Q form two edge points of that sub beam.

Would you agree that you can apply the theory of "example 1", here too?
Yes, it's *exactly* the same method as demonstrated in example 1 above !

You see: often in math, one has to be a bit cunning to approach problems.
It's not intelligence at all. Once you have seen it "one time", you can apply it to nummerous other tasks.

3.2 Distances:

Main Theory:

Here we will see about the "distance" between 2 points. Let's first see how we handle this in R²,
that is, the familiar 2 dimensional XY coordinate system.
Take a look at figure 10 below.

Figure 10: The distance between two points in the XY plane.

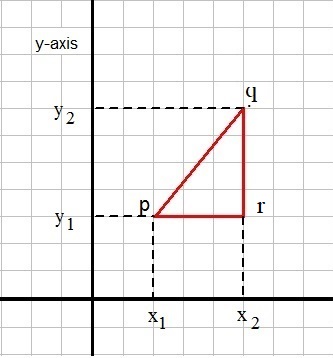
We see two points, "P" and "Q". Ofcourse, you will reckognize a right angled triangle, and the
hypothenuse represents the shortest distance between "P" and "Q".

But do you also notice that we can express the distance in coordinates?
Let me explain:

Suppose:

P is the point (x₁, y₁), (like for example (2, 3), but it could have been any point).
Q is the point (x₂, y₂), (like for example (5, 7), but it could have been any point).

If you look at figure 10, then indeed P and Q have the coordinates (2, 3) en (5, 7).

The length PR is 3. You can easily see that in fig. 10. Do you notice that this also holds for x₂-x₁ = 5-2 =3 .
The length RQ is 4. You can easily see that in fig. 10. Do you notice that this also holds for y₂-y₁ = 7-3 =4 .

We know that:

PQ² = PR² + RQ², => PQ = √ (PR² + RQ²).

This is equivalent to:

PQ² = (x₂-x₁)² + (y₂-y₁)² =>

PQ = √ ( (x₂-x₁)² + (y₂-y₁)² )

This holds in all cases. So, if you have any two points P=(x₁, y₁) and Q=(x₂, y₂),

Then the distance "D" between those points is:

D_pq = √ ( (x₂-x₁)² + (y₂-y₁)² )

Task: try to calculate the distance between two points P and Q in figure 10.

In 3 dimensional space, it's no difference at all, except that we have one extra coordinate.

The distance PQ between the two points:

P=(x₁, y₁, z₁ ) and Q=(x₂, y₂, z₂)

is:

PQ = √ ( (x₂-x₁)² + (y₂-y₁)² + + (z₂-z₁)² )

Example:

What us the distance "D" between the two points P=(3,6) and Q=(-2,-5)?

D = √ ( (-2 - 3)² + (-5 - 6)² ) = √ ( (-5)² + (-11)² ) = √(25+121) = √146 = (about) 12.

Example: Distance between a line and a circle.

This time, we want to calculate the distance between a line and a circle.
If you see a task like that, most often people actually mean the distance between the line and the center of that circle.
We need to find the point of the line, "closest" to the center of the circle. Then, we can simply apply the theory
of the theory above.

Obviously if you look at such a line, there can only be one point on that line which really has the shortest
distance to the center of that circle.

As an example of such a situation, see figure 11 below.

Figure 11:

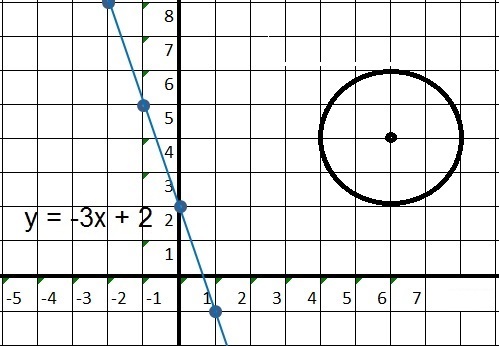
We have:

-The line L₁: y=-3x+2
-The circle with it's center at (6,4) and radius "r" is 2.
How to approach this? One line of thinking is this:

- We might be able to construct the line L₂ which is perpendicular to L₁,
and let it also go "through" (6,4).

- Next, if we have L₂, then we might be able to find the intersection of L₂ with L₁.

If we would succeed, we then have two points, for which we must calculate the distance between them.

From note 4, we know that if two lines are perpendicular, then "slope_of_line1 * slope_of_line2 = -1".

So, the equation for the line which is perpendicular is: y=⅓x + b. We still need to find "b".
We know that y=⅓x + b must pass through (6,4), so we can use that to determine "b":

4 = ⅓ * 6 + b => b=2.

The equation for L₂ is: y = ⅓x + 2.

If we can find where y = ⅓x + 2 intersects with y = -3x + 2, then we find the second point (next to
the first point (6,4)). Then we can easily calculate the distance between them.

Finding where L₂ intersects with L₁:

⅓x + 2 = -3x + 2 => 3⅓x = 0 => x=0. If x=0, then use either of the two equations,
to calculate the corresponding "y". Let's take y=-3x+2. For x=0, then y=2.

We finally have our two points for which we must calculate the distance between them: (0, 2) and (6, 4).

Can you calculate the distance yourself?

Chapter 4: Surface area's and Volumes of some common objects in Geometry.

Yes, we are going to look at some Surface area's (of 2D objects), and Volume calculations (of 3D objects),
of a number of common objects.

It's certainly true: the stuff in this chapter is not "shocking" at all.

It's really easy. In some tasks, having the formulas for Surface area's and Volume calculations at hand,
can be important.

4.1 Surface area's:

In figure 12 below, you see a rectangle of length "L" height "H". In this case, L=10 and H=3.
The units of L and H are not given, so it could be in meters, centimeters, or feet etc...
If the units are not given, you simply focus only on the numbers themselves.

Figure 12:

What we see above, are two identical rectangles, both with L=10 and H=3.
The one on the right side, is also divided in elementary "surface units". If we count them all,
the total number will turn out be "30". It does not surprise us, that this is equal to "L*H".

It should all be rather trivial to us. The nice thing is, that many other objects, with any form
of symmetry, will fit rather nicely in a rectangle, or square, and if we do that, we will
see that the surface area of such an object equates to "factor * L*H". Such a factor could be e.g. ½.

Let's see some common examples:

- Geometric diamond:

Figure 13: Geometric diamond

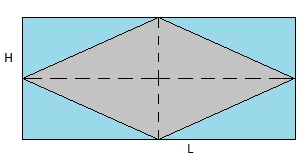
Above we see a geometric diamond. A requirement for a 2D object to qualify as a diamond,
is that all 4 sides are of equal length. As you might also notice, is each angle and it's opposite angle,
have the same value.

In the figure above, I also drawed a rectangle surrounding the diamond. You probably have not much
trouble in agreeing with me, that the Surface (S) of the diamond, is exactly half that of the rectangle.
There exists "proof" of this, but we are going to skip that. I know it sounds a bit simple: but if you
look at it, you know it's correct. Thus:

S_diamond = ½ * L * H

where L and H are the length and height of the enclosing rectangle.

The dotted lines inside the diamond are called the "diagonals". Let's call them d₁ and d₂.

You probably have noticed that d₁ and d₂ have the same magnitude as L and H.
So:

S_diamond = ½ * d₁ * d₂

Example: Suppose we have a diamond where d₁ = 3 cm, and d₂= 4 cm, then S = ½ * 3 * 4 = 6 cm².

- Triangle:

Figure 14: A few triangles (green area's)

Althoug a triangle looks so simple, there exists a tremendously amount of valuable theorems on triangles.
We are going to see a couple of them later on.

But what about the Surface area? I will apply the same trick as with the "diamond" above.
However, instead of Height and Length, with a triangle (in the context of surface calculations),
one of the sides (usually displayed "on the ground") is called the "base b", and the "height h"
is the length of the side perpendicular to "b".

If you look at figure 14 above, I have 3 examples. In each occasion, you can see that again
the surface area of the triangle, is exactly half of the rectangle.

S_triangle = ½ * b * h

Example: Suppose we have a triangle with b = 8 m, and 3₂= 3 m, then S = ½ * 8 * 3 = 12 m².

- Circle:

The area of a circle is π r², with "r" the radius of that circle.. It's an amazing result.
Using an integral, it's not hard to prove this. In note 8, we have seen how to calculate integrals.
But there are many other ways to prove it.

It should be intuitive too. The only "parameter" where the Surface area of a circle can be dependent of, is "r".
A circle is completely symmetric. There is absolutely nothing on the graph of a circle, that stands out
in some way. It's fully symmetric. The area can indeed only depend on the radius "r".

If you would inflate a certain circle, then only "r" grows, and indeed the area (and circumference) grows too.

S_circle = π r²

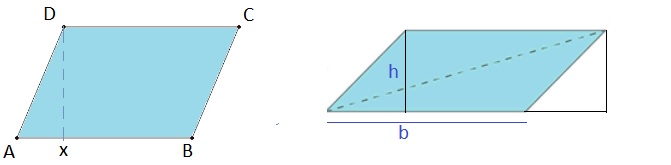
- Parallelogram:

For this object, the requirement is that we have "two sets" of parallel lines, where the lines
in each set, are equal in lenght. See figure 15 below.

Figure 15: Parallelogram

If you like, you can punish your brain with the following questions:

-Can see say something about opposite angles?
-Can you say someting about the angles connected by one side?

Take a look at the first subfigure in Figure 15. Do you notice, that you might "shift" the triangle AXD
to the right, which then forms a rectangle?

So, for a parallelogram, the surface area "S" is:

S_{parallelogram} = b * h

where "b" is one side, and "h" is the height of the corresponding line perpendicular to "b".

4.2 Volumes:

Ofcourse, it's impossible to take a look at all 3D objects. So, just let us review a couple
of such objects.

In figure 16 below, we see a sort of (unofficial) "archetype" of volume calculations. We see a 3D beam.
Take notice of the "unit of volume", that is, the small blue box in the right lower corner of that beam.

Figure 16:

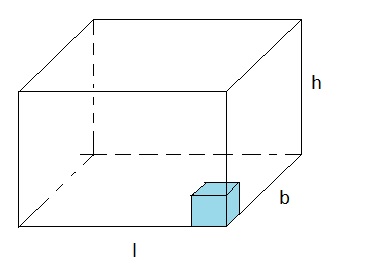
If you would stack them up, first to the left, then in all the other directions, you will count to (l * b * h).
Indeed, the "volume" of the larger beam is (l * b * h) number of "units of volume".

Ofcourse, the dimensions (l, b, h) of some 3D object will not always be a nice integer number
of "units of volume", like l=5 etc...
But so what? You might find for some beam that it's volume is 6 * 2 * 3.45 = 41.40 cm³.
In such a case, l=6 cm, b=2 cm, and h=3.45 cm. Instead of "cm", it could have been "feet", or "yards", or "meters" etc..

For a cube with side "l", the Volume=l³. For any beam with side "l", "b", and "h", the Volume=l*b*h.

- Pyramid:

Well, there are multiple types of pyramids, like one having a rectangle at it's base, or a triangle at it's base.

-rectangle at it's base:

Figure 17: Pyramid (rectangle at it's base).

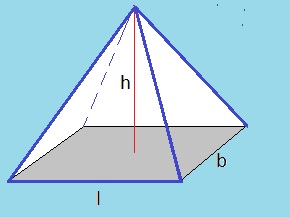
If you have a pyramid with rectangle at it's base, and you would surround it by a beam, you would see that
it's Volume is only ⅓ of the Volume of the beam. So:

V_pyramid-rb = ⅓ * l * b * h

Note that if the Surface of the base rectangle is "A", then the upper equation is equivalent to:

S_pyramid-rb = ⅓ * A * h

-triangle at it's base:

Here we will simply list the formula:

V_pyramid-tb = ⅙ * l * b * h

- Sphere:

Again, this is a completely symmetrical object. Nothing on it's surface stands out.
If you would inflate a smaller sphere, "r" increases in the x-, y-, and z-directions.
Maybe you find it plausible that the Volume depends on "r" only, and that's it, actually.

V_sphere= 4/3 π r³

- Cone:

Figure 18: Cone (with a circle at it's base).

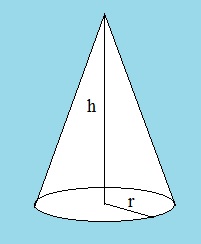
A cone has a circle at it's base. So, the surface area "S" of the base circle is S = π r²,
where "r" is the radius of that circle.

Suppose a cone has a height "h", from the base, to it's top.
Then the volume of the cone is:

V_cone= ⅓ * h * πr² = ⅓ * h * S_{base circle}

Those sorts of formula's can be proven, and it's even not so difficult to do so.
But, I only like to have in this text some illustrations of some common objects, and their associated volumes.

Example:

Suppose a cone has a height "h" of 7 centimeter, and a radius of 3 centimeter of the base circle.
What is it's volume in cm³ ?

V = ⅓ * 7 * π3² = (about) 65.94 cm³

Chapter 5: A few important Theorems on triangles.

Since a triangle is such a common object in Geometry, and also in exam questions, I like to review
some important Theorems, and properties, with triangles.

5.1 Relations between sides (constant ratio), in two similar triangles:

The following Theorem provides us with tools, to calculate unknown sides from similar triangles.

Similar triangles have the same shape, but may differ size (and ofcourse, they usually do).
When two triangles, have two same angles, they are similar. Ofcourse, since all angles add up to 180 degrees,
the third angle in both, must be the same too.

In order to establish if two triangles are similar, it's sufficient to find two equal angles in both triangles.

Figure 18: Two similar triangles.

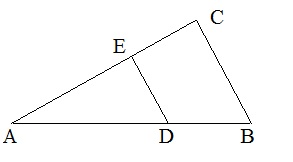
Triangle ABC is similar to ADE. We can see "by the eye", that this is obvious. How to prove it?
We need to find two angles in both, which are the same. The first one, is obvious. ∠A is common
to both triangles. Secondly, ∠D is equal to ∠B, due to the "F rule/F shape".
Thus: Triangle ABC is similar to ADE.

Now, here is the toolkit: for similar trangles, the ratio between corresponding lines is the same
for all lines in the triangles.

Take a look at figure 18 again. If you inflate the smaller triangle, all corresponding lines
will increase with the same ratio. Suppose AB=8 and AD=6, AC=7. What is AE?

Using this "ratio rule" we get:

AB
--
AD

AC
--
AE

8
--
6

7
--
AE

AE = 5.25

5.2 The sine and cosine rules in arbitrary triangles:

The sine rule:

The sine rule we mean here, is applicable for any arbitrary triangle.
It does not have to be a right angled tiangle. This is great for calculations.

Ofcourse, we already have seen definitions for the sin(), cos() etc.. in a "right angled" triangle,
for example, we have seen that in note 4.

But now, we mean a new rule.

Take a look at figure 19 below.

Figure 19: Just some triangle with sides a, b, c and angles α, β and γ .

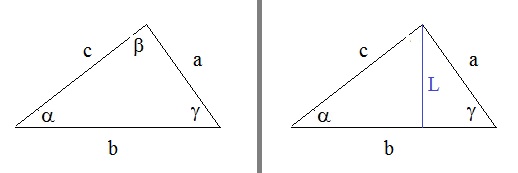
Take a look at the first subfigure. We have line "a" opposite to α, line "b" opposite to β,
and line "c" opposite to γ.

If you know two sides, and two angles, and you want to quickly calculate the unknown side or unknown angle,
then you can use the "sine rule":

a
---
sin(α)

b
---
sin(β)

c
---
sin(γ)

In the formula above, you see "three parts", but obviously you can use it for only "two parts" too,
like the equation using "a, sin(α), b, sin(β)".

Proving this rule is quite simple. Take a look at the second subfigure. Here I drew line "L",
which is perpendicular to the base of the triangle. Note that now you can see two right angled triangles,
for which we can use the orinary sin definition.

Using the common definition for the sin, we have:

sin(α) = L/c => L = c sin(α)
sin(γ) = L/a => L = a sin(γ)

Thus: c sin(α) = a sin(γ)

Thus: c / sin(γ) = a / sin(α)

Such a proof can be used for the other line and angle too.

Example:

Lets take a triangle that looks like figure 19. Suppose c=20, b=15, and γ = 55 degrees.
Question: calculate β.

20
---
sin(55)

15
---
sin(β)

=> 20 /0.82 = 15 / sin(β) => sin(β) = 0.61.

It's great that we have a value for sin(β). But we need β. So we use the sin^-1 function:

β = sin^-1(0.61). For the answer, use your calculator. Ofcourse, for this, you need to know
how to put the sin^-1 at work. I admit, sometimes that is a small chalenge.

However, it's the method which is important here. I you get that, all is fine.

The cosine rule:

The sine rule is pretty simple to proof, and fortunately, quite simple to remember too.

The "cosine rule" is just a tiny bit more difficult to proof, and to remember.
But just as the "sine rule" is, the "cosine rule" can be enormously helpful in calculating
unknown sides, or angles, in arbitrary triangles.

Please understand that both the sine and cosine rules, work for arbitrary triangles.

We can use figure 19 again, as a reference figure. Here are the cosine rules:

a² = b² + c² - 2bc cos(α)
b² = a² + c² - 2ac cos(β)
c² = a² + b² - 2ab cos(γ)

Maybe they are not so difficult to remember after all. Example given:

If you want (a certain side)², then sum the squares of the other sides, -2 times "product other sides", times cos(opposite angle).

Often it is used if you know two sides, and the angle they close in, and you want to know the other missing side.
In that case, you know the opposite angle (thus cos too), and the two other sides.

Example:

See figure 20 below.

Figure 20: One example on how to apply the cosine rule.

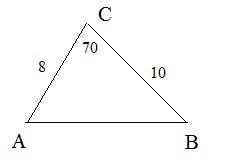
We know the lengths of the sides AC and BC. We also know the angle that those lines include, namely 70 degrees.
What is the length of side AB?

AB² = 8² + 10² - 2*8*10 cos(70).

The further calculation is work for the calculator.

Well, to apply the cosine rule is indeed that simple.

Basic arithmetic/calculus. In the series: Note 20.

Subject: Geometry

This note is especially for beginners. Maybe you need to pick up "some" basic "mathematics" rather quickly. So really..., my emphasis is on "rather quickly". So, I am not sure of it, but I hope that this note can be of use. Ofcourse, I hope you like my "style" and try the note anyway.

Chapter 1: Lines in vector representation.

1.1 Vector representation of a line in 2 Dimensional space (R2)

1.2 Vector representation of a line in 3 Dimensional space (R3)

1.3 Intersection of 2 lines in 2 Dimensional space (R2)

1.4 The perpendicular vector, to some vector.

Chapter 2: Representation of a flat surface in 3 Dimensional space (R3).

z = ux + vy + h (u,v,h are some constant numbers)

ax + by + cz = d (a, b, c, d are some constant numbers)

Chapter 3: Some further applications of the Pythagorean theorem.

Some further applications:

3.1 Application in 3D objects:

Example 1:

Example 2:

Example 3:

3.2 Distances:

Example:

Example: Distance between a line and a circle.

Chapter 4: Surface area's and Volumes of some common objects in Geometry.

4.1 Surface area's:

Sdiamond = ½ * L * H

Sdiamond = ½ * d1 * d2

Striangle = ½ * b * h

Scircle = π r2

Sparallelogram = b * h

4.2 Volumes:

Vpyramid-rb = ⅓ * l * b * h

Spyramid-rb = ⅓ * A * h

Vpyramid-tb = ⅙ * l * b * h

Vsphere= 4/3 π r3

Vcone= ⅓ * h * πr2 = ⅓ * h * Sbase circle

Chapter 5: A few important Theorems on triangles.

5.1 Relations between sides (constant ratio), in two similar triangles:

5.2 The sine and cosine rules in arbitrary triangles:

Basic arithmetic/calculus.
In the series: Note 20.

This note is especially for beginners.

Maybe you need to pick up "some" basic "mathematics" rather quickly.
So really..., my emphasis is on "rather quickly".

So, I am not sure of it, but I hope that this note can be of use.
Ofcourse, I hope you like my "style" and try the note anyway.

1.1 Vector representation of a line in 2 Dimensional space (R²)

1.2 Vector representation of a line in 3 Dimensional space (R³)

1.3 Intersection of 2 lines in 2 Dimensional space (R²)

Chapter 2: Representation of a flat surface in 3 Dimensional space (R³).

S_diamond = ½ * L * H

S_diamond = ½ * d₁ * d₂

S_triangle = ½ * b * h

S_circle = π r²

S_{parallelogram} = b * h

V_pyramid-rb = ⅓ * l * b * h

S_pyramid-rb = ⅓ * A * h

V_pyramid-tb = ⅙ * l * b * h

V_sphere= 4/3 π r³

V_cone= ⅓ * h * πr² = ⅓ * h * S_{base circle}