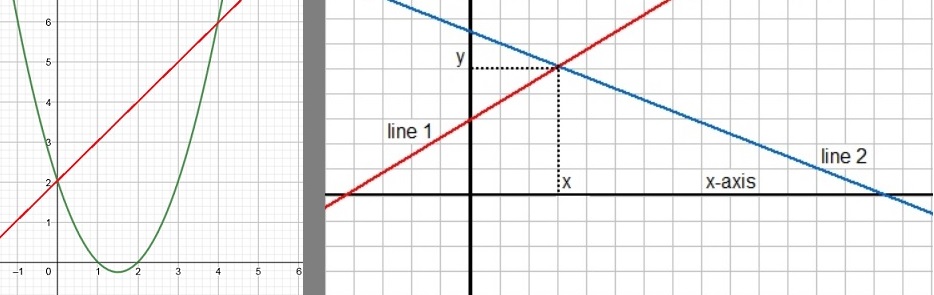
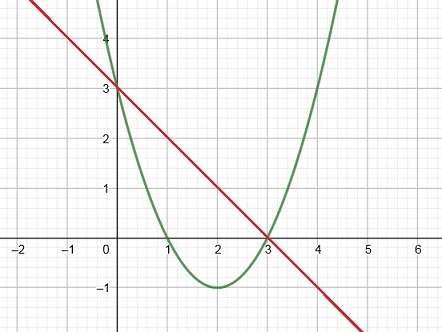
So, let's find the intersection first:
2x - 6 = -3x + 4 => 5x = 10 => x=2.
If we fill in "x=2" in either of the equations, we find the corresponding "y".
Let's use the first one: "y=2x - 6". Then y=2*2-6=-2.
Thus, the lines intersect at the point (2,-2). However, we only need the "x" value,
we already have found before, namely "x=2". The question was: for which x values is
the line f(x)=2x-6, above the line g(x)=-3x + 4? So, finding the "y" value was not needed after all.
It's reasonable to use, say x=3 as a test value in f(x)=2x-6. This gives 2*3-6=0.
Now insert it in g(x)=-3x + 4. This gives -3*3 + 4 = -9 + 4= -7.
Thus for x=3, we have indeed that it is true that 2x - 6 > -3x + 4.
Thus the solution for "2x - 6 > -3x + 4" is "x>2".
So, the method above is not very complicated.
-But let's use algebra only:
For the example above, we have:
2x - 6 > -3x + 4
=>
5x > 10
=>
x > 2
You see that? Without any drawing of graphs, we immediately have found "x>2".
One thing to beware of: multiplying or dividing by a negative number:
When we have some sort of inequality, and during solving, we need to multiply or divide
both sides of "<" or ">", by a negative number, then:
"<" becomes ">".
">" becomes "<".
Example:
Suppose we have:
7x + 5 < 9x + 4
add -5 to both sides (or some say: bring 5 to the other side, and flip sign).
7x < 9x – 1
add -9x to both sides (or some say: bring 9x to the other side, and flip sign).
Now we are left with:
–2x < –1 => -x < -½
As usual, we like to have it in the for "x=", instead of "-x=".
Just think about it: for what "-x", would it be smaller than -½?
Suppose "x=1" (the plus 1), then would it be true? Fill it in: -1 < -½? True.
-x < -½
multiply both side with "-1", and flip the "<" to ">".
x > ½
Another example of solving inequalities.
Figure 6. The costs that three companies charge you for phone services.
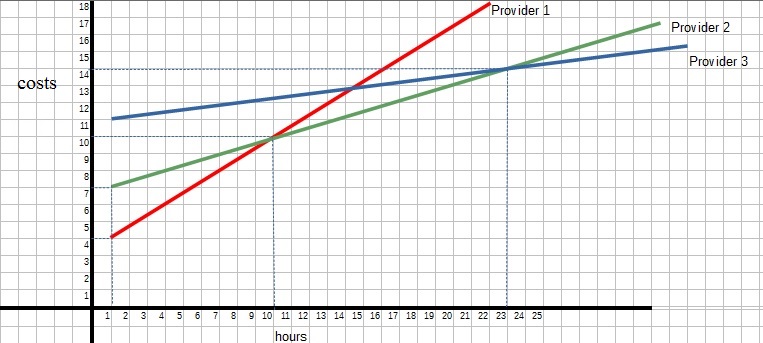
If you use a cell phone, the costs are dependent on how many hours you use your phone.
In the figure above, we see the graphs of "costs per hour" that 3 different providers
would charge you.
The y-axis represents the costs, and the x-axis represents the numbers of hours you
use you phone.
Question: which provider is the cheapest?
There is not "one" answer, because if you study the figure above, there are different x intervals
for which a certain provider would be the cheapest one.
Could you work this out, that is, finding the x intervals which identifies the cheapest provider?
The next two sections are optional reading. You may skip this, if you want to follow my series.
7. Quadratic functions and relations.
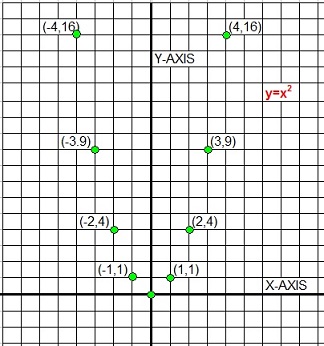
The equation "y=ax2 + bx + c" is also called a funcion because every "x" is mappedto exactly one "y". This is just an "agreement" among mathematicians, established a long time ago.
You can take a look at the parabola we have shown sofar, and it's true. For each x on the x-axis, you find only 1 "y".
By the way, if you have equations like "y=ax+b", or "y=ax2 + bx + c", then those are quaranteed to fullfill
the "rule" that every "x" is mapped to exactly one "y" only.
You can see that very clearly with a line defined by "y=ax+b". There really is just one "y" for every specific "x".
In such cases, people also write y as y = f(x), where f(x) is for example "ax+b". The "f" then suggests,
that we are dealing with functions.
But not every relation between "x" and "y" is a function. Take a look at figure 4:
Figure 7. An example of a "circle" and "ellips".
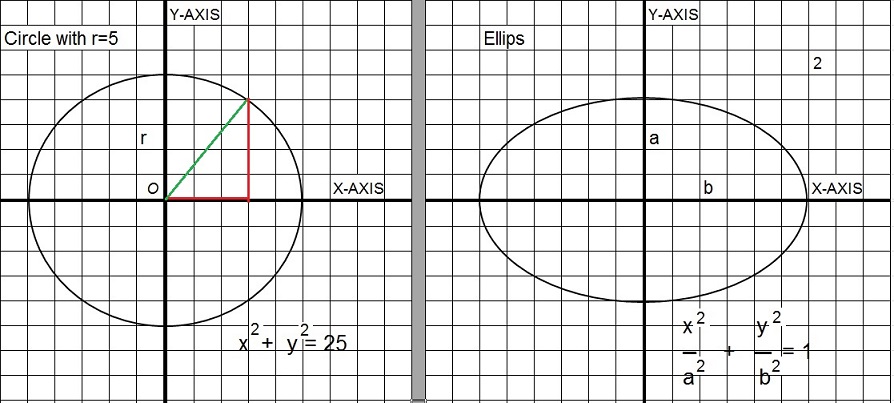
If you look at the circle, you will see that any "x", is mapped to 2 "y's".
For example, x=3 is mapped to y = 4 and y = -4.
For this reason, the circle is not described by a function, but by a "relation" between x en y.
For a circle centered around the "origin" (where x-axis and y-axis comes together), the relation is:
x2 + y2 = r2
Where "r" is the radius of the circle. Since a circle is fully symmetrical, if I prove the equation for a few
x's en y's, then you probably "believe" the equation is right.
Well, for example, take a look at the circle in figure 4. For that circle, the radius "r" is 5. So r2 = 25.
For the point (5,0) holds: 52 + 02= 25 + 0 = 52 = 25. This is true.
For the point (-5,0) holds: -52 + 02= 25 + 0 = 52 = 25. This is also true.
For the point (0,5) holds: 02 + 52= 0 + 25 = 52 = 25. This is also true.
Alright, these were special points. But now, for example for the point (3,4). Does the relation then holds too?
If you look closely, you will see that (3,4) sits on the circle, so this is true. Now, let's calculate:
32 + 42 = 9 + 16 = 25
Right again.
For points on a circle (centered around the origin), "x2 + y2 = r2" is always true.
Maybe you see the "connection" with the famous Pythagorean theorem.
Let's focus on the point (3,4) again. It's on the circle. In figure 4, you can see that the length of y = 4,
and the lenght of x = 3. You notice the right-angled triangle shown in figure 4?
For the point (3,4), the equation "x2 + y2 = r2" is simply the same as the Pythagorean theorem.
Actually, if you think about it, you can always create (or imagine) such a right-angled triangle for any point on the circle.
8. Higher order polynomials.
We have seen linear equations, and quadratic equations up to now. The are of the form:y=ax+b
y=ax2 + bx + c
But, ofcourse, higer powers of "x" are possible too. Let's see a simple function of "x" to the power of three.
We also often hear that the "degree is three".
y=ax3
Or, in a general format:
y=ax3 + bx2 + cx + d
Sometimes, equations of a certain degree, are also called "polynomials" of that degree (like 3).
Usually, in basic math, these sorts of equations are "left alone", like in the sense of finding
intersections with the x- and y-axis.
So I won't tought them here either. But I like you to know about them.
By the way, the point where such higher-degree function crosses the y-axis, is very simple to calculate.
Because, at that point, neccessarily (as always) x just has to be 0.
So: for the intersection with the y-axis:
y=ax3 + bx2 + cx + d, and if x=0, it means: y=a03 + b02 + c0 + d = d.
So the point where the curve hits the y-axis is (0,d).
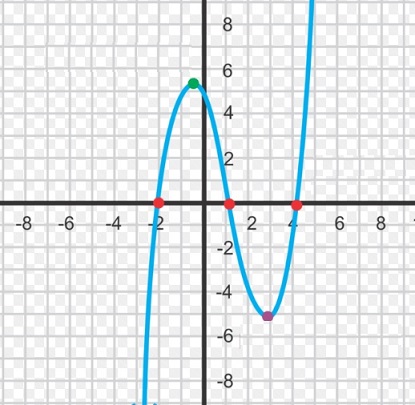
Since y varies mainly with ax3, usually, the function "climbs or sinks" really fast.
For example, if we look at the simplest one, namely "y=x3", then when x=6, y already is 216.
You might like to Google on the shape of polynomials of the 3rd degree. They often have one "top" (maxima),
and one "crest" (minimum), and tend to rise or sink steeply with larger (positive or negative) "x".
But depending on the values of the coefficients (a, b etc..) their shapes can vary enormously.
(Some polynomials of the 3rd degree, with specific coefficients, do not have a distinguished maxima or minima).
Figure 8. An example of a polynomial of the 3rd degree.
Optional reading (you absolutely don't have to):
You don't need to memorize the following.
Indeed, the following might look pretty awkward at first sight. But really, it not so difficult at al.
We might thus also have "n" th degree polyniomials
For example, in a very general form:
y=anxn + an-1xn-1 + ... + a1x + c
So, we might have one of the fourth degree:
y=a4x4 + a3x3 + a2x2 + a1x1 + c
Note that the usual coefficients like a,b, and c, are replaced by numbers designated as an, an-1 etc..