This note is especially for beginners.

Maybe you need to pick up "some" basic "mathematics" rather quickly.
So really..., my emphasis is on "rather quickly".

So, I am really not sure of it, but I hope that this note can be of use.
Ofcourse, I hope you like my "style" and try the note anyway.

There are several methods to solve integrals.

-absolutely learn the basic primitives (the standard functions and their primitives).
-investigate if it is possible to rewrite the integrand to something simpler.
-the method of "substituting".
-apply the "reverse differential" chain rule.
-the method of "integration by parts".
-you must know the most important goniometric and logarithmic identities.
-and other techniques.....

⇒ For some goniometric integrals, the following table of values may help:

Rad	degrees	sin	cos
0π	0	0	1
1/6π	30	1/2	1/2 √ 3
1/4π	45	1/√2	1/√2
1/3π	60	1/2 √3	1/2
1/2π	90	1	0

Section 1. The f(x)=a/(bx+c) types, or f(x)=(ax+b)/(cx+d) types.
Thus functions using only the first power of "x". What is F(x)?:

First, you know that the primitive of f(x)=1/x, is F(x)=ln|x|.

You must really learn some basic functions, and it's primitives, by heart.

In general, functions as listed in the title above, immediately smell like having some form of "ln" function
as it's primitive. Take a look at these examples:

Example 1:

f(x)

=

1 ------ (3x-5)

It will have as it's primitive, the function:

F(x)= ⅓ ln|3x-5| + C

This is true, since if we take the derivative, we have ⅓ . 3 . 1/(3x-5)
where the "3" factor comes from the chain rule, which explains why we need to insert the ⅓ factor.

Example 2:

f(x)

=

(3x+7) ------- (3x-2)

Let's try this:

f(x)

=

(3x+7) ------- (3x-2)

=

(3x-2+9) ---------   (3x-2)

=

1+

9 ----- (3x-2)

And we know how to find the primitives of those 2 terms. So F(x) is:

F(x)=x + 3 ln|3x-2| + C

Note that finding the primitive of 1/(ax+b) terms can be also be found using "substitution",
which we will study a bit later.

Example 3:

f(x)

=

(2x+6) ------- (x+4)

We have unlike x terms in the nominator/denominator. Let's try this:

f(x)

=

(2x+6) ------- (x+4)

=

2

(x+3) ---------   (x+4)

=

2

(x+4-1) ----- (x+4)

=

2

(

1+

-1 ----- (x+4)

)

=

2

+

-2 ----- (x+4)

And we know how to find the primitives of those 2 terms. So F(x) is:

F(x)=2x + ln|x+4| + C

Section 2. Fractions with all sorts of x^m terms (m=1, 2, 3 etc..) in
both the nominator and denominator:

These can be really intimidating, depending on the complexity.

-However, first quickly try to see if you can simplify the expression, since possibly
you might be able to decompose nominator/denominator in "factors", which can be eliminated,
that is, "gummed away" from the nominator/denominator.

-You can also perform a "tail division" just like with arithmetic.

-You might be able to use substitution.

-You might be able to split the fraction into multiple terms.

-Other ways, like using the chain rule, integration by parts etc...

Example 4:

Suppose we have:

f(x)

=

4x4+4x3+x2+3 ----------------     2x+1

Then ∫ f(x)dx seems a real challenge.

There are several ways to handle this. You might try a "tail divison".

2x+1 / 4x⁴+4x³+x²+3 \ 2x³+x ² + x
---------4x⁴+2x³
---------2x³+x²
---------------------
---------2x²+x

with a remainder of "3".
This way, we have:

f(x)

=

4x4+4x3+x2+3 ----------------     2x+1

=

2x3+x2+x+

3 ---- 2x+1

This way, we see that the integral

∫f(x)dx

=

∫ (

4x4+4x3+x2+3 ----------------     2x+1

) dx

=

∫ (

2x3+x2+x+

3 ---- 2x+1

) dx

And we know how to handle each of those terms, including the 3/(2x+1) term (see example 1).

Example 5:

Suppose we have:

f(x)

=

x -------- dx (1+x2)3

Find the primitive of f(x). Note that you may also write f(x) as f(x) = x.(1+x²)^-3.

We must somehow find a format, so that it fits the chain rule.

Note that d/dx (1+x²) = 2x.
Note that x = 1/2 . 2x
Note that the primitive of (...)^-3, then must have a (...)^-2 part.

It's not that we follow a very specific rule to get to our objective, but it might
be seen that F(x) is:

F(x) = -(1/4) . (1+x²)^-2 + C.

In effect, I have used the chain rule. I indeed reckognized it as applicable.
If you would take the derivative of F(x) = -(1/4) . (1+x²)^-2, you would get
f(x) again.
So, If you reckognize a function that can be viewed as f '(g(x)).g'(x) (disregarding any constants),
then the primitive is f(g(x)).

Example 6:

Sometimes, you can split the fraction in multiple terms.

Suppose we have:

∫f(x)dx

=

∫

x2+3 -------- dx   2x

We can split this into:

∫ f(x)dx

=

∫

x2+3 -------- dx 2x

=

∫

x2 --- dx 2x

+

∫

3 --- dx 2x

Where we can deal with both terms with the knowledge presented above.

Section 3. Functions with ln(x), and/or e^x, and/or a^x.

You know that the derivative of e^x, is e^x.
Thus, the primitive of e^x, is also e^x.
It's a simple fact, and we are going to use that in various places.

Example 7:

Let's try to find: ∫ e^kxdx, where k is some constant.

Let's substitue u=kx. Therefore du=k dx. Thus (1/k)du=dx.

So, ∫ e^kxdx = ∫ e^u(1/k)du = (1/k)∫ e^udu =(1/k)e^u+C=(1/k)e^kx+C.

Example 8:

Let's try to find: ∫ 2^xdx. (this excercise is also model for a^x)

If ^gLog(x)=y, then g^y=x. Thus g^Log(x)=x.
Thus:

e^ln(2)=2

∫ 2^xdx = ∫(e^ln(2))^xdx = ∫(e^{ln(2) x})dx

Now, set u=ln(2)x. Thus du=ln(2)dx. Thus 1/(ln(2) du =dx.

Let's substitute that: ∫(e^{ln(2) x})dx=1/ln(2) ∫e^udu = 1/ln(2) e^u +C.

Let's subsitute u=ln(2)x back:

1/ln(2) e^ln(2)x +C = 1/ln(2) (e^ln(2))^x +C = 1/ln(2) 2^x +C.

You can generalize this to:

The primitive of f(x)=a^x is:

F(x)

=

1 ---- ln(a)

ax + C

Example 9:

Find the primitive of f(x)=xlinx

Here you might use the technique of "integration by parts".

It's based on the product rule of derivatives: (fg)' = f'. g + f. g'

You can always rearrange the expression into something like   f'.g = (fg)' - f. g'

Now you can integrate both sides of the equation. So, if you see a f' for which you can
easily find the primitive, and a "g" for which you can easily find g', then the trick may work.

Example using integration by parts:

∫ x linx dx = 1/2 x² lnx - ∫ 1/2 x² . 1/x dx = 1/2 x² lnx - 1/4 x² + C.

Example 10:

Find the primitive of f(x)=ln(x)

Again, using integration by parts:

∫ ln(x) dx = ∫ 1 . ln(x) dx = x ln(x) - ∫ x . 1/x dx = x ln(x) - ∫ 1 dx = x ln(x) - x + C

Example 11:

∫ x.e^x dx = x.e^x - ∫ e^x . 1 dx = x.e^x - e^x + C.

Above, again, we used integration by parts.

So, if f(x)=x.e^x, then F(x) is:

F(x)=x.e^x - e^x + C.

Section 4. Functions with goniometric terms (sin, cos, tan etc..).

Here, we better know a few goniometric identities. This might make life much easier
when solving such integrals. We will see them later on. First:

-Good stuff #1:

We know that:

If f(x)=sin(x) then the derivative is f '(x)=cos(x)

If f(x)=cos(x) then the derivative f '(x)= -sin(x)

Thus:

∫ cos(x) dx = sin(x) + C

∫ sin(x) dx = -cos(x) + C

Now, if we just put the constant "a" as a factor at "x", then we have:

If f(x)=sin(ax) then the derivative is f '(x)= a cos(ax)

If f(x)=cos(ax) then the derivative f '(x)= -a sin(ax)

Thus:

∫ cos(ax) dx = (1/a) sin(ax) + C

∫ sin(ax) dx = -(1/a) cos(ax) + C

If you take the derivative of say sin(ax), you know that you must use the chainrule,
which explains why we have the "a" in "a cos(ax).

For the other way around, finding the primitive, thus explains that we need the factor (1/a),
to cancel out the "a" factor.

-Good stuff #2:

-An important identity is:

sin²(α) + cos²(α) =1

On the unit circle (r=1), this is true, since x=cos(α) and y=sin(α),
and using the Pythagorean theorem, we see that it is correct.

-An important identity is:

sin(2x)=2sin(x)cos(x).

There are many ways to proof it. One way, is to use geometry, using triangles and circles.
Clever folks, who did that, then simply found that:

sin(A+B) = sinAcosB + cosAsinB

Thus:

sin(x+x) = sin(x)cos(x) + cos(x)sin(x) = 2sin(x)cos(x)

Many identities exist, with accompanying proof, which you easily can find on the Net.
As of now, here the mathematical proofs will be omitted.

-Another important identity is:

cos(2x) = 1-2sin²(x) = cos²(x) - sin²(x)

-Another important identities are:

cos²(x) = ½ (1 + cos(2x)).

sin²(x) = ½ (1 - cos(2x)).

Example 12:

Suppose we have f(x)=sin³(x). What is F(x)?

First, note that sin³(x)=sin(x).sin(x).sin(x)=sin(x).sin²(x).

Now, in a former note we have seen that sin²(x) + cos²(x) =1.

Thus: sin²(x)=1-cos²(x).

So: sin³(x) = (1-cos²(x)).sin(x).

Now, d/dx (cos(x))=-sin(x). Thus d(cos(x))=-sin(x)dx.

Thus:

sin³(x)=(1-cos²(x)).sin(x)=(1-cos²(x)).-d(cos(x))
=
(cos²(x) - 1)d(cos(x))

Now, we use the "substitution trick": u=cos(x).

Note the "smart step" of using du = d(cos(x)). This we can immediately fill that in
in the equation above.

Then we get:

(cos²(x) - 1)d(cos(x)) = (u² - 1) du.

∫ (u² - 1) du = 1/3 u³ -u +c

Thus:

∫sin³(x) = 1/3 cos³(x) -cos(x) +c

Above looked a bit like a fuss. Could we not have used directly u=sin(x)?
Yes, but you still needed to worry about du=cos(x)dx and use that into the new equation.

Example 13:

This should be an easy one.
Suppose f(x)=sin(3x). Then what is F(x)?

From the "Good stuff #1" section above, we can immediately see that:

F(x)=∫ sin(3x)dx =-1/3 cos(3x)+C

Example 14:

Suppose:

f(x)=sin²(x)
g(x)=cos²(x)

Task: Find the primitives F(x) and G(x).

No, it's not difficult. From the section "Good Stuff#2", we have seen that:

cos²(x) = ½ (1 + cos(2x)).

sin²(x) = ½ (1 - cos(2x)).

And those are easy to solve. For example:

F(x)=∫ sin²(x)dx = ∫ (½ (1 - cos(2x)) dx = ½x - ¼sin(2x) + C

Example 15:

Solve:

∫ sin⁵(x)dx

We might use the following approach:

∫ sin⁵(x)dx = ∫ sin(x) sin⁴(x)dx = ∫ sin(x) (sin²(x))²dx =

∫ sin(x) (1 - cos²)²dx

Now, use u=cos(x) => du= -sin(x)dx

Then we have:

∫ -(1 - u²)²du = ∫ -(1 - 2u² + u⁴)du

This is easy to solve:

F = -u + (2/3)u³ - (1/5)u⁵ + C

Substituting back:

F(x) = -cos(x) + (2/3)cos³(x) - (1/5)cos⁵(x) + C

Section 5. Some special cases, and Volume Integrals.

Example 16:

Suppose we have a bathtube, where the surface at any height x, is determined by:

C(x)=2500x^0.5-70x (in cm²)

The max height of the bathtube is 50cm.

Can it hold 500l of water?

∫₀^p C(x)dx = ∫₀^p [2500x^0.5-70x]dx=

[(2500/1,5) x^1.5 - 35x²]₀^p  =

(2500/1,5) p^1.5 - 35p² - 0 = (2500/1,5) p^1.5 - 35p²

This must be equal to 500l . We have that 1l=1000cm³. Thus 500l=500.000cm³.

Thus (2500/1,5) p^1.5 - 35p² = 500000

Thus p=49.9

Example 17:

Fig 3. The area defined by the boundaries x=a, x=b, and f(x) and g(x),



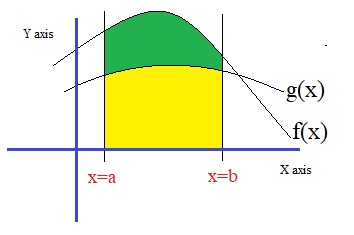
Often, at math Highschool exams, you may see tasks as the one listed below.

Suppose, over the domain [x-a, x=b] we have two functions f(x) and g(x).
Calculate the surface determined by the boundaries x=a, x=b, the x-axis, and which lies between
f(x) and g(x).

In this case, the question is about the size of the green area A_Green. See the figure above.

Thus:
A_Green = ∫_a^b f(x) dx - ∫_a^b g(x) dx

Note that we must always do "upper area - lower area".

Let's do a simple example. Say we have the line f(x)=4x+2, and the parabola g(x)=x²+2.
We do not have "a" and "b", so we must find the x value(s) of the intersection(s) first:

x²+2=4x+2 => x(x-4)=0 => x=0 or x=4.

The line is above the parabola, between x=0 and x=4, and for x>4, the parabola above the line.
The area we need to calculate, is thus in the interval 0<=x<=4.

We have ∫₀⁴ (4x+2) dx - ∫₀⁴ x²+2 dx =

[2x² + 2x]₀⁴ - [1/3³ + 2x]₀⁴ = 10.7.

Example 18: Calculating a Volume.

Imaging the function f(x)=√x. If you do not know how "the function looks like",
then look it up.

Now, imaging that we rotate the graph along the x-axis, over 2π. A tree dimensional object
is created, which looks like a 3D parabola, with the x-axis as it's center line.

If you would chop up the object over small Δx, we get small objects looking like small cilinders.

The volume of such small cilinder, at a certain location x_i, is approximated by

π (f(x))² . Δx_i (like "π r² . h", for a cilinder with width "h").

If you would add all those small cilinders, in an interval [x=a, x=b], you obtain the Riemann sum
which is a close approximation for the total Volume over the interval [x=a, x=b].

Thus, a definite integral exists, if Δx_i gets infinitsemal.

Suppose we want to calculate the Volume in [x=0, x=4], we have:

∫₀⁴ π(√x)²dx = 8 π

That's it. Hope you liked it !!!