In the series: Note 9.
Subject: Complex numbers.
Date : 10 March, 2016Version: 0.2
By: Albert van der Sel
Doc. Number: Note 9.
For who: for beginners.
Remark: Please refresh the page to see any updates.
Status: Ready.
This note is especially for beginners.
Maybe you need to pick up "some" basic "mathematics" rather quickly.
So really..., my emphasis is on "rather quickly".
So, I am really not sure of it, but I hope that this note can be of use.
Ofcourse, I hope you like my "style" and try the note anyway.
This note: Note 9: Complex numbers.
Each note in this series, is build "on top" of the preceding ones.
Please be sure that you are on a "level" at least equivalent to the contents up to, and including, note 8.
This note will be a very short note on Complex numbers.
1. Main sets of numbers, and why compex numbers.
It seems, numberwise, that we already have everything covered ! We have powers of any kind of number, square roots like √ 3,fractions like 2/7, "floating" numbers with a "." (dot, or comma) like 4.56287, numbers like π (which never end behind the ".") etc.. etc..
Not entirely so, as we will see in a few minutes. But first, let's see what exactly we have right now, and try to classify them.
1.1 The common classifications:
Since a long time ago, mathematicians have classified and labeled "sets" of main types of numbers.As you know, there exists a large variety of numbers, like "whole numbers" (1, 2, 7, 1000 etc..),
fractions like 1/3, 2/7 etc.. and "real" numbers which seems to include about "everything".
These classifications, are often viewed as infinite sets. The main sets are:
N: the set of "Natural numbers", which is {0,1,2,3, etc...}
Here, we have positive numbers only.
Z: the set of "whole numbers" or integers, which is {..., -3, -2, -1, 0, 1, 2, 3, etc...}
They can be positive or negative.
Q: the set of "fractions" or "Rational numbers", like for example -1/7, 2/3, 8/10, 9/1000 etc..
Don'y forget. Even integers are "Rational numbers", since we can always represent them as a fraction, like 3/3, 10/2, 27/9 etc..
-: the set of "IrRational numbers", which are numbers which cannot be written as a fraction, like e.g. √3
R: the set of "real numbers", which is all of the above, but also including numbers like π, "e" etc...
Note: there are a few more sets, but the most important ones are listed above.
These are all pretty "normal" numbers. There are many mathematical rules for operating on those numbers.
Let 'a' be one of such normal numbers. For example, we never have allowed that a2 is negative.
Really! In ordinary calculus or arithmetic, we have always assumed, or required, that a2 ≥ 0.
Now, sometimes we need to climb over some fence or barrier, to enter new territory.
1.2 The set of Imaginary numbers "bi":
However, what do you think of the next set: The "Imaginary" numbers? It probably looks strange at first sight.The following holds (or is defined/required) for Imaginary numbers:
the square of an imaginary number is "negative".
That is not compliant with the usual rules of engagement in arithmetic. Using numbers from N all the way up to R,
we always have required:
a x a ≥ 0 for any number we know in from N all the way up to R.
But, an "imaginary number" is defined as bi, where i2= -1.
Thus we might have the number 3i, and the square of that number is (3i)2 = 32 * i2 = 9 i2 = -9.
in effect, you may say that the square of bi is equal to -b2.
Pretty Strange isn't? We will understand it better when we see complex numbers.
1.3 A "pictorial" representation of number sets:
Let's take a look at the illustration in picture 1:Figure 1. Number sets
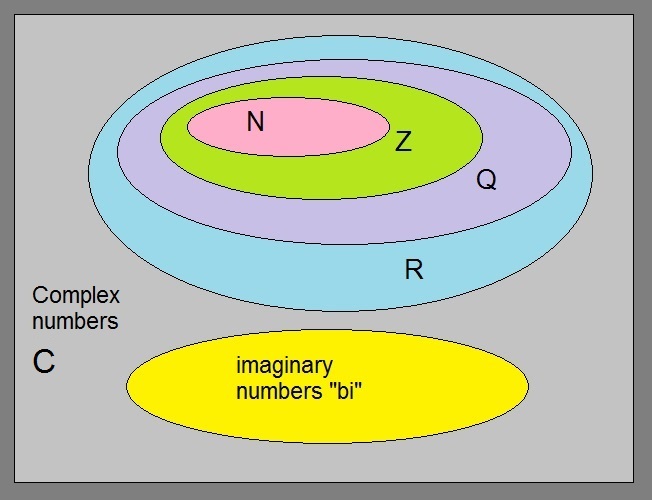
You should read figure 1 this way: Z encloses N (Z is bigger than N), but Q encloses Z, and R encloses everything.
Well everything? No, since the "imaginary numbers" are alien to the "normal" numbers, they are set apart.
In figure 1, you see the yellow ellips to illustrate that the are completely seperate from the rest.
Now, since scientists (like mathematicians and physicists) are completey "un-stoppable", they created a new set
of numbers: The complex numbers.
In figure 1, you see the square. In fact, it is everything inside the whole of figure 1.
Now, if you take a real number (from R), say "a", and multiply it with an imaginary number, say "bi",
then we have nothing new, since a x bi = ci (where axb=c), which is just an imaginary number again. That's nothing new.
However, if you take a real number (from R), say "a" and add it to an imaginary number, say "bi",
then we get a two dimensional construct "z":
z = a + bi
In a manner of speaking: the imaginary numbers are alien to the real numbers. We have no other choice, thanto represent the real numbers along the x-axis (as we already always did), and represent the imaginary numbers
along the y-axis. So, along the x-axis we have the usual arrangement of real numbers, just as we have seen many times before
in all those plots of functions in former notes.
Along the y-axis, we have the "bi" numbers, where b is a real number (and can vary in the usual way),
and i is that strange object for which holds that i2= -1.
The only point both axes intersect, is at (0,0) since then even an imaginary number is '0', if b=0.
Do we end up in something familiar? Yes, it all looks pretty much the same as the familiar XY plane we have seen so many times before.
So, instead of z=a+bi, we might just as well use "x" for "a" and "y" for "b", and so we have:
z = x + yi
Note that iy=yi. Some Folks are just more familiar with writing "z=x+iy" instead of "z=x+yi", but it's the same anyway.So we have complex numbers in the form of "z = x + iy". Note that both 'x' and 'y' are "real" numbers
The "iy" part, is the imaginary part. Indeed, it's the "i" which makes "iy" rather special.
Some obvious observations:
If y=0, then we have z = x + iy = x + i0 = x, which is just a common "real" number.
If x=0, then we have z = x + iy = 0 + iy = iy, which is just an imaginary number.
If x=0 ∧ y=0, then we have z=0. Viewed from the perspecive of the common XY plane,
z=0 corresponds to (0,0) and that corresponds to "the origin" (O) of the XY coordinate system.
1.4 Why complex numbers?
(i):Probably, the following is very important. In general, it is argued by almost all mathematicians,
that complex numbers are truly more fundamental than real numbers. In a sense, a real number is simply no more
than a special case of a complex number (namely, when y=0).
Complex numbers have been proved to be a fantastic generalization of numbers.
Although complex numbers seem to make things more complex, it's really the other way around !
As an example: some horribly complex differential equations, or integrals, from the presepctive of "R",
are greatly simplyfied using complex function theory.
(ii):
In physics, since a long time, it's an essential element in most theories.
For example, Quantum Mechanics would not be the same theory without complex numbers.
Actually, there would not be such a theory at all.
My "focus" here is on "math", but in note 10, we will see some examples from physics.
2. The complex XY plane, and some algebra.
In figure 2.1, you see a few complex numbers in a XY coordinate system.For example, note the number z = 2+5i, and for example the number z = -6 -i.
You see? It's really easy to plot complex numbers in a XY coordinate system, if you know 'x' and 'y'.
Figure 2. Complex numbers represented in a XY coordinate system.
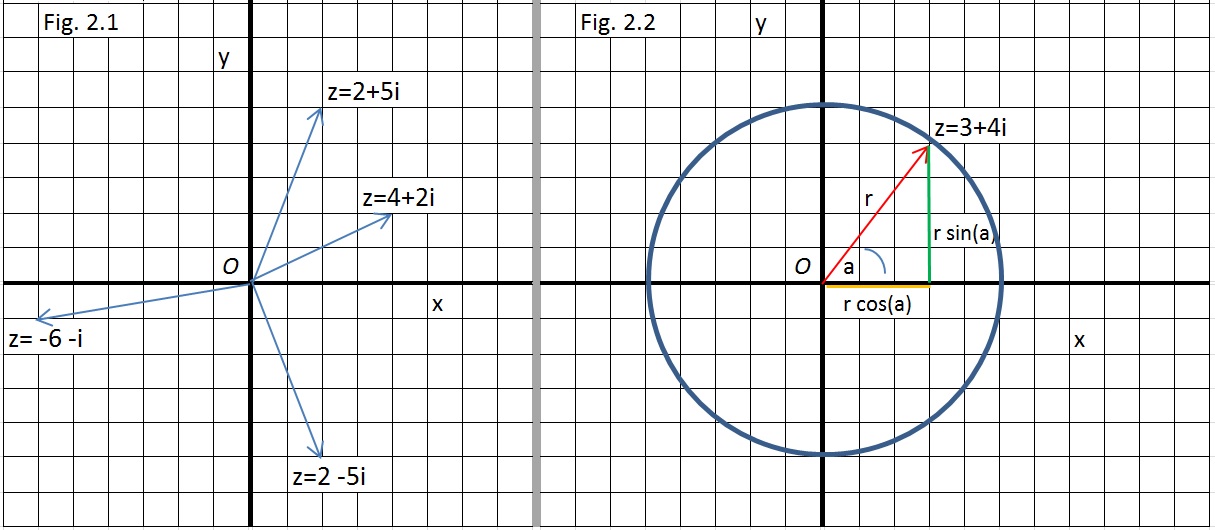
If you are familiar with 2 dimensional vectors, in a 2 dimensional Cartesesian coordinate system,
then indeed, it looks strikingly similar, but there are some differences.
If z=x+yi, you may, if you like, express it as point (x,y). However, keep in mind that "yi" is the
imaginary part of 'z', so that is not evident if you simply express 'z' as "(x,y)".
So, usually, it's not done that way, unless it's "handy" for some situation.
2.1 The Complex conjugate of a complex number:
In figure 2.1, you see the number z=2x+5i. As if that number is "mirrored" through the x-axis, you mayalso note the number 2x-5i. That one is called the complex conjugate of "z".
This fact can be important in later notes. The complex conjugate is often written as z with a small "-"
above the letter, or with an asterix as a superscript, like z*.
In general:
If z=x+yi then it's complex comjugate is z*=x-yi.
Note that if z=z*, then it must be a real number, that is, it's on the x-axis, and "yi"=0, thus y=0.
2.2 The "absolute value", or the length, of a complex number:
The "absolute value" is actually equal to the length of the number "z". You may interpret it as the distanceIn fig. 2.2 you see a picture that illustrates, that "x" and "y" and "r", always form a right angled triangle.
Here, the 'x' and 'y' then form 2 sides of that right angled triangle, and the hypotenuse is 'r'.
The "length" of r, is the "absolute value" (or it's length, or the distance to "O") of the complex number.
We can apply the "Pythagorean theorem" here, which states:
r2=x2 + y2
From note 4, we know that x=rcos(α) and y=rsin(α), if "α" is the angle between r and the x-axis.If needed, please check note 4 again, because I think this is very important to understand.
Thus:
r2=x2 + y2 = (rcos(α))2 + (rsin(α))2
= r2 ( cos(α)2 + sin(α)2 )
We already have seen in note 4, that r2 can be eliminated from both sides of the "=",and thus we again have cos2(α) + sin2(α) = 1
In general, people say that the lenght, or absolute value of the number z, notated as |z|, is:
|z|2=r2=x2 + y2
Thus:|z|=√ (x2 + y2)
2.3 z expressed as rcos(α) + rsin(α) i
From figure 2.2, we know that we may express z in a sum of rsin(α) and rcos(α) too.x = rcos(α)
y = rsin(α)
Thus:
z = x + yi = rcos(α) + rsin(α) i
If r=1, then "z" is on a circle with radius 1, and z= cos(α) + sin(α) i2.4 Euler's equation:
Having knowledge on how polar coordinates work, may also help to understand "Euler's equation".We have not dealt with anything else than "Cartesian coordinates" yet, which is like the XY plane having perpendicular
x- and y-axes. Indeed, you can perfectly "pinpoint" any number "z", by specifying the 'x' and 'y' values of z=x+yi.
There exists ofcourse a number of ways to mathematically "prove" Euler's equation. We are not going to do that yet,
since I will do it as a "special case" when we have a note on "coordinate transformations".
In that note (on "coordinate transformations"), the equation will get clear in a more natural fashion.
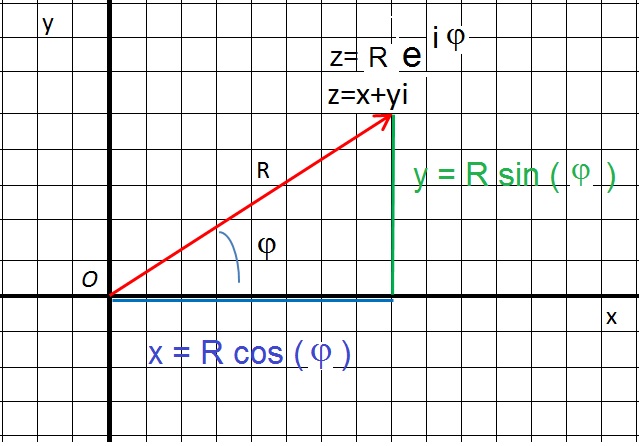
Here is Euler's equation. You only have take notice of the fact that it exists, and it's often used in many other derivations.
z = r eiφ =r cos(φ) + rsin(φ) i
At both sides of the '=', the factor 'r' is present, so we may eliminate it. The equation then becomes:eiφ = cos(φ) + i rsin(φ)
So, to "describe" or "pinpoint" any number "z", we may use:
- z=x+yi (Cartesian coordinates: the real values x and y fully pinpoint the number "z").
- z= r eiφ (the distance "r" of "z" to the Origin, and the angle between "r" and the x-axis,
fully pinpoint the number "z".
- z = r cos(φ) + r sin(φ) i (which was shown in section 2.3).
fully pinpoint the number "z".
Figure 3. Different ways to describe, or pinpoint, "z".
Ofcourse, there is much more to say on "complex numbers".
However, in my "series of notes", this will do for now.