with respect to each other.
For example, you can be stationary in frame S, which, as far as you can judge, is in rest.
Then you watch frame S' passing by, which moves along with a constant speed.
The direction to which S' is moving, is not so relevant. It could be along your +y direction,
or the direction defined by (1,-2,3) or whatever else direction. It does not matter at all.
The only requirement we need in this chapter, is that the relative speed between S and S', is constant.
For the purpose of this chapter, any direction where S' is moving to, is OK.
So, for simplicity, we can simply just assume that S' moves along your +x direction.
Let's further assume that S' moves with 5 m/s (relative to S).
Note that an observer in S', might say that it is frame S, which is moving with 5 m/s to the -x direction.
Let's assume that S uses the coordinates (t,x,y,z) and S' uses (t',x',y'z').
From a classical viewpoint, you might say that it is completely absurd to speak of t and t', since time
is the same everywhere, in any moving frame of reference. This is so true from a classical standpoint.
However, for the spatial coordinates, it is a bit different, and fully normal from a classical viewpoint.
Suppose, in your system S, you describe the point A by (5,2,5), meaning x=5, y=2, z=5.
That point will stay stationary, according to an observer in S, and it will be the same set of coordinates,
no matter what.
However, an oberver in frame S', sees point A moving with a constant speed in the -x direction.
So, let's just suppose that at a certain moment, S and S' exactly coincide, and then ofcourse, as S'
further moves to the +x direction, the observer in S' thinks that the position of point A is indeed (5,2,5)
when the two frames coincide. However, as time passes, the position of A (according to the observer in S'), will be
(0,2,5) when 1 second has passed, (-5,2,5) when 2 seconds has passed, (-10,2,5) when 3 seconds has passed etc.. etc..
Note that the observers in S and S both see that the "y" and "z" is the same for both frames.
Its' not too hard to see that:
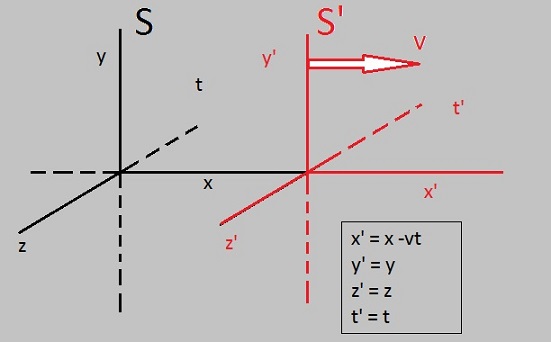
x' = x - vt
y' = y
z' = z
t' = t (equations 1-4)
For the spatial coordinates (x,y,z) or (x',y',z'), these relations must be true.And indeed, by using classical logic, it must also be true too, that t'=t.
The set of equations above, is often referred to as a "Galilean Transformation".
Figure 1. Frame of Reference S', moves with speed "v" (along the x-axis) relative to S.
1.2 Invariance of Physical laws under Transformations.
You have to admit this: if physical laws are different in S and S', we would have a real problem.
The observer in S simplys says that it is S', which is moving with 5 m/s to the +x direction.
The other observer in S' (who thinks that his/her reference frame is in rest), tell us that it is S which
is moving with 5 m/s in the -x direction.
Who is right? Impossible to say.
But fundamental physical laws have to be the same. So, conservation of Energy, conservation of momentum,
F=ma, or the laws of Maxwell (electrodynamics) etc.. etc.., have to be invariant.
A well-know example is to look "how good" F=ma will hold under transformations.
Let's say that a mass "m" is in space, where S and S are in too. Let's suppose a force F acts upon that mass.
You thus might say:
An observer in S says that F=ma holds.
An observer in S' says that F'=m'a' is true.
Since in a classical sense, mass is the same in any frame of reference, we then go for:
An observer in S says that F=ma holds.
An observer in S' says that F'=ma' is true.
This is so since, from a classical perspective, mass is not dependent on velocity. For example, in a flying plane
an object has the same mass as when it was still on the runway.
The whole of classical mechanics, treats mass as a constant. We don't know any better that that.
So what we want to know is, is:
F=ma
the same as:
F'=ma'
Thus: is it true that F' = F?
Let's try this:
F' = ma'
=
m
d
--
dt'
dx'
--
dt'
=
m
d
--
dt'
d (x-vt)
-------
dt'
(equation 5)
If we now in the classical sense, think that t=t' for the Space where the frames S and S' are part of,
(which is a logical and very resonable assumption), then in equation 2 above, we replace t' with t.
F' = ma'
=
m
d
--
dt
d (x-vt)
-------
dt
=
m
d
--
dt
d x
--
dt
-
m
d d (vt)
-------
dt dt
=
m
d2 x
-----
dt2
=
ma
=
F
(equation 6)
Note that the term in "red" "d / dt ( d(vt) / dt )" is "0", since "d(vt) / dt" is "v", which is constant, and d/dt of a constant, is zero.
So, F=F' in all frames of reference which move with a constant speed relative to each other.
The above reasoning is just an example. It is not too hard to "prove" that e.g. conservation of momentum, and oher classical laws,
are invariant for a Galilean Transformation.
1.3 Addition of velocity vectors (or speed) from a classical viewpoint.
Suppose you are sitting in a train which has a speed of 50 m/s, relative to the track.
Now you start walking in the train, with a speed of 5 m/s in the direction of the front of the train,
then your speed relative to the track (or relative to the surface of the Earth) is 50 m/s + 5 m/s = 55 m/s.
We can simply keep all the examples "one dimensional" here, that is, the speed of an object
is along the direction of a moving frame of reference.
As another example:
Take a look at figure 2 below.
Figure 2. In this example S' is moving in the +x direction with 20 m/s, relative to S.
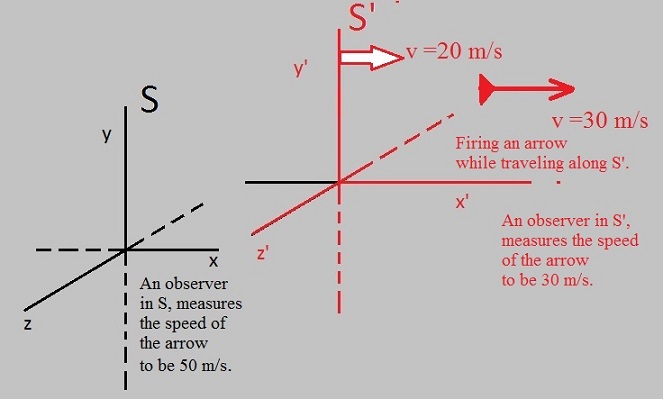
In this case, an observer in S sees that frame of reference S', is moving with 20 m/s into the +x direction.
So, "everything" in frame S' (including bow and arrow), is moving with that speed, relative to S.
However, since an "abosute" frame of reference does not exist, the observer in S' might simply say that
it is S which is moving into the -x direction with 20 m/s.
Now, suppose the observer in S', shoots an arrow with 30 m/s (relative to S') into the +x direction>
So in S' people would say: the arrow goes with 30 m/s into the +x direction.
But the observer in S measures the speed of the arrow to be 50 m/s. This sum is simply the initial (constant) speed
that the arrow already possesed, and the extra 30 m/s due to the power of the bow.
But this is already we all know what is true. We see it in daily life all the time.
Indeed, in classical mechanics we simply add the speeds, when the object (like the arrow) and the frame of reference
are moving in the same direction.
Now, the startling thing is, that this does not work with ElectroMagnetic radation, like radiowaves, light, x-rays etc..
In this case, such "radiation" travels with "c" (the speed of light), and "c" only.
So, suppose frame S' is moving with 0.7 c with respect to frame S. The observer in S', now fires a laser in the same
direction as S' is moving to.
For observers in S and S', that signal simply has a speed of "c".
So, for an observer in S, the speed of the signal is not 0.7c + 1.0c=1.7c
The speed of "c" (the speed of light) seems to be completely unrelated to the speed of any observer.
This is rather "un-classical".
Let's try to see what scientists did in the past, both on a theoretical and experimental basis, to finally
reach the conclusion that the speed of light is "constant".
Chapter 2. Speed of light.
2.1 A few Experimental observations:
The speed of light in true vacuum, called "c", is just slightly below 300000 km/s (3 * 108 m/s).
It is absolutely fenomenal that a Danish astronomer (Romer), already in 1676 determined that the speed is somewhere about 225000 km/s.
He used the eclips of the moon "Io" around Jupiter. The Earth revolves around the Sun in one year ofcourse.
In that orbit, in a period of half a year, we have (so to speak), a near "spot" and far "spot" with respect to
the line of sight with Jupiter.
By comparing the time difference at such eclips, at moments that the Earth is near or far, Romer came to his conclusion.
Note how ingeneous that was.
Ofcourse, at much later years, the speed was determined with increasing accuracy.
Around the mid of the 1800's, Maxwell created a theoretical framework decribing ElectroMagnetic (EM) phenomena in general,
including EM waves.
Somwhere around 1886, Hertz conducted a number of experiments which proved the actual propagation of EM waves
in "free space" (wireless).
Up until the year 1900 (or thereabout), folks still were convinced that ElectroMagnetic radiation (like visible light),
needed a fixed medium, the "ether" (or "aether"), for "propagation".
Indeed, all "waves" observed on a human scale, like the travelling waves in water if you drop a rock in a pond,
are propagating ocillations that use a "medium" for their expansion. Countless of other of such observations exists.
It was quite reasonable in those days, that the same sort of thing must be true for EM waves too.
The "Michelson and Morley" experiments.
One of the first "cracks" in the idea of a fixed "ether", arose with the experiments of Michelson and Morley.
Ironically, those researchers actually did the experiment, with the expectation that it would prove the existence of such an "ether".
If light and other EM radiation, uses a fixed and absolute frame of reference of some substance, called the "ether",
then using an ingeneous experiment might prove it to be true.
Again, it was used that the Earth revolves around the Sun, with an orbital speed of 20 km/s.
Now, in a span of 6 months, the speed of the Earth is opposite than it was 6 months before.
If light travels in an absolute frame, then small differences in the speed of light might be observed, due
to the different speeds of the Earth in 6 months difference.
The experiment was indeed set up in such a way, that differences would be greater than the experimental margins of error.
However, no difference was found !
By the way, in later years the experiment was often repeated, using different setups, with ever increasing accuracy.
In the years close to 1900, it is indeed true that physicists who were involved in this field, we quite puzzled.
Today, countless experiments and observations (including astronomical observations) have been done, and all confirm
that the speed of light is constant, and independent of the speed of the observer.
Note how "un-classical" this is, with respect to traditional classical mechanics.
The "Gedanken" experiment of Einstein.
Einstein passed away in 1955. However, some footage exists where we can hear the master talk.
I forgot a lot of details, but when I was fairly young, a saw a documentary of Einstein,
where he told the viewers of a rather remarkable moment in his early life, way before he published any of his theories.
In a tram, in Bern (Swiss), he watched a clocktower showing a certain time. Einstein then suddenly pondered that the light
of that particular moment, that particular image of the clock, "would be captured", "or frozen" in some way, traveling for ever.
As if time itself was frozen or was halted.
It seems that such event contributes to the early thoughts Einstein had, about Space and time.
While still not so exact as he would formulate it later on, but it seems that already in that tram,
Einstein felt that Space and time are not fully seperate, but connected in "SpaceTime".
As it turned out later on, a "SpaceTime interval" between two events will always has the same "distance",
no matter which frame of reference is used.
Exactly this, will be explained in Chapter 3.
2.2 A few Theoretical considerations:
Transmission of Information:
The relevancy that the "speed of light" is the "ultimate speed", and is always the same, independent of the frame of reference,
has "shifted" somewhat, for some scientists, to a (sort of) newer interpretation.
While it still is very true, I think that somewhere around the '70's, the "tone" shifted to that it is
actually the "transmission of information", which cannot exceed the speed of light.
The difference is quite a subtle one. As we will see later, an important thought is that "causality" must be preserved,
and that is also governed by means of how information can be "distributed" (so to speak) among processes and events.
As to how fast an individual "pure sine like" wave travels, is not so relevant: it contains no information.
Information "sits" in how (for example in EM waves) frequencies or amplitudes are modulated in carrier waves.
An individual "harmonic", or pure single wave, among a "group", might theoretically" even go faster than "c".
Before you say that this is an absurd statement, listen to this: some physicist believe that for example in an experimental setup,
where two very long metal sheets are very close, that inside, the amount of quantum fluctuations are somewhat less compared
to the "normal" vacuum (Casimir effect). They argue, on theoretical grounds, that the speed of light then might an extremely small
fraction higher than in regular vacuum c.
But at the same time, it is shown that it does not hold for information transmission.
So, it does not matter at all. Einsteins law is not breached.
Keep in mind that the latter alinea is fully theoretical, and is never tested or proven.
Many physicists also reject such a line of thought, while some still persist in such a view.
But when considering all of this from the perspective of "transmission of information", the case is settled
and done with anyway.
Speed of light in a "medium":
In matter (or a medium), the speed of light is slower than "c". For example, in water
the speed is be only 0.75c (where c is always the speed in vacuum).
In a way, the speed is only apparently lower, since from an "atomic" or "Quantum Mechanical" view,
the photons "collide" with the electrons of the atoms of the material, en gets re-transmitted again.
Overall, that consumes time, and is considered to be a fair explanation, among physicists.
Ofcourse, there is more to say on that, than only the couple of lines above. However, it does not affect
the way we must view "c" in the framework of STR.
The Vacuum:
The "true" speed of light, as the absolute constant, is considered to be in "vacuum".
There are still some "uncertainties" as to what the vacuum exactly is. For example, the concept of "vacuum fluctuations"
where virtual particles "pop up" from the vacuum, and destroy each other again, are considered very seriously in several
disciplines of Physics.
As to "how" this would have any effect on the speed of light, is "really" still not fully covered.
Also, it is generally expected that "c" has to be involved/connected with the fundamental structure of the Vacuum,
or SpaceTime, whether the best theory would turn out to be "superstring theory", or "Loop Quantum Gravity", or something else.
This too is still not fully covered by any theory sofar.
Other fundamental constants which depend (or relate) on (with) c:
Vacuum permittivity of Electric- Magnetic fields:
There is a relation that couples "c" to 2 fundamental electrical and magnetic constants of the Vacuum, namely
ε0 and μ0 which represents the "vacuum permittivity", or "permittivity of free space".
These constants say "something" about the capability/ability of the vacuum to permit electric- and magnetic fields.
c2
=
1
---
ε0 μ0
Whether the relation is truly fully exact, still seems to be a subject of debate among physicists.
Also, a correct and fully satisfactory interpretation of the relation, seems to be missing still, although such
a view is not shared by all physicists.
However (in SI units), those constants ε0 and μ0, keep on returning in every fundamental equation of Maxwell's
Theory of Electrodynamics.
A dielectric material, shows a certain permittivity too, which can be related to the polarization or orientation
of charged particles. For the electric field, such a permittivity can then be expressed as ε = εmε0
I am not suggesting that "c" can be exactly calculated from ε0 and μ0, or the other way around.
It's just such an equation that couples constants, and it seems to suggest that a constant "c" is a property of the Vacuum.
I have to confess that I like such discussions, and that is probably the reason why I have put it here.
That probably holds even more for the following subsection.
But you are strongly encouraged (by me) to do some further explorations on this facinating subject.
Planck's Length:
I am not going to say anything here, about the Planck's Length. But I think it will add "something"
to the discussion about the speed of light, why it is always constant, and why it is so important.
If "Planck's Length" really is unknown to you, you might consider to do a websearch, and read some articles.
You won't regret that, I am sure.
If you see the relation which defines the length of Planck and which connects it to fundamental constants, then ask yourself
what possibly the role of "c" can be here.
However, it's not neccessary for this note.
Chapter 3. Minkowski SpaceTime and Distance.
Let's spend a few words on the "Minkovski SpaceTime", since it plays an important role in the approach to STR.
But first, let's recapitulate a few properties of "common" vectors (like in R2, R3),
like the "length" or magnitude of an ordinary vector, and the "distance" between points.
3.1 Small Recap on lenghth/distance of vectors in flat Euclidean space:
- The "length" or magnitude of an ordinary vector in a Cartesian coordinate system of a flat Euclidean space:
The "magnitude" of vector A is often denoted as |A|, but some other notations go around too.
In a orthonormal Cartesian coordinate system, the calculation of the magnitude is done like in the following examples:
In R2, the length of vector A is |A|=√(x2 + y2)
In R3, the length of vector A is |A|=√(x2 + y2 + z2)
In RN, the length of vector A is |A|=√(x12 + x22 + .. + xN2)
- The "distance" between two points (vectors) in a Cartesian coordinate system:
You can view this stuff in multiple ways. You can say that we "just" have two points P and P', and the line segment
which connects those two points, clearly determines the distance between them.
Or rather equivalent: You can also say that we have a vector P and vector P', and the length of the vector P-P',
simply is the distance to these points defined by P and vector P'.
Some examples:
-In R2:
|PP'|2 = (x2 - x1)2 + (y2 - y1)2
Thus:
|PP'| = √ ( (x2 - x1)2 + (y2 - y1)2) )
-In R3:
For R3, we simply have one additional coordinate. So, we would have:
|PP'|2 = (x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2
Thus:
|PP'| = √ ( (x2 - x1)2 + (y2 - y1)2) + (z2 - z1)2) )
-In Rn:
Suppose we have two points "P" and "Q" in Rn, with the coordinates:
(p1, p2, .. ,pn) and (q1, q2, .. ,qn)
then:
|PQ|2 = (p1 - q1)2 + .. + (pn - qn)2)
Thus:
|PQ| = √ ( (p1 - q1)2 + .. + (pn - qn)2) )
In general, a "distance", is quite often denoted by "S" or "s", or in infinitesemal form "ds".
3.2 Minkowski SpaceTime:
Minkowski SpaceTime is a four-dimensional space, 3 spatial coordinates an one additional time coordinate.
You can view it like "just" "another" a four-dimensional space ofcourse, but that's not really the plan.
It is meant specifically to specify events, possibly linked by "lightsignals".
Such an event from a viewpoint of Physics, is for example an observer (or source) sending a lightpulse,
and another observer recieving that lightpulse.
This then would form a connection, or a distance, between those two events (points).
It's that simple.
A point, or event, in Minkowski SpaceTime can be notated as (x1,x2,x3,x4).
However, to give it a better physical interpretation, write it as (x,y,z,ct), since then it is clear that we have indeed
the usual 3 spatial coordinates and one time coordinate.
But why "ct"? Since Minkowski SpaceTime connects events, it's usefull to use "ct", since that defines the standard unit,
that light travels, measured over a standard time, which actually then "functions" as a component distance, just like "x", or "y" etc..
Now, we may have a point, and another point, over which we can easily define a "distance" between those points.
What can be a "reasonable" formulation of a distance in Minkovski SpaceTime? It will have some similarity with
the familiar Euclidean case, but this time the "path" of a lightsignal must be incorperated too.
Let;s try this:
If we have the two events (x1,y1,z1,ct1) and (x2,y2,z2,ct2),
then the ordinary spatial distance would be: √ ( (x2 - x1)2 + (y2 - y1)2) + (z2 - z1)2) )
but that must equal the distance covered by the lightpulse: c(t2 - t1).
This is why often the distance is covered (so to speak) by the equation:
c2(t2 - t1)2 - (x2 - x1)2 - (y2 - y1)2 - (z2 - z1)2 = 0 (equation 7)
Formally, equation 7 is called "the interval", which is "0" in every frame of reference.
Equation 7 has some similarities to the "Pythagorean theorem" rewritten as:
c2-a2-b2=0
Based on such ideas, the distance "ds" in Minkowsky SpaceTime can be found to be:
ds2=c2dt2-dx2-dy2-dz2 (equation 8)
Actually, this possibly expresses the "core" idea of STR. Since "c" is constant in all moving frames of reference,
the Minkowsky distance between events is always the same.
Remember that an event might be viewed as an observer (or source) sending a lightpulse, and another observer recieving that lightpulse.
This distance, between those two events, is the same as viewed from any frame of reference.
So, in Minkowski spacetime, all observers in all frames of reference will agree on the distance in SpaceTime between events.
However, it still needs to be "proven" in a mathematical way, and ofcourse we want to find the equivalent
of the Galilean transformation in this relativistic perspective, like expressing x' in terms of x and t.
As you might already see from equation 8, if a Minkowski distance ds is required to be constant, then in a moving frame of reference S',
a clock must go slower, and some spatial distance (in the direction of motion) must contract, otherwise ds will not
be the same as viewed from frame S. I try to prove that (or better: I try to make it plausible) in Chapter 4.
We are up now for some highlights of the core of STR.
Chapter 4. The core: Lorentz Transformations and STR.
4.1 The relativistic Transformations or the Lorentz Transformations:
Einstein took the following "assumptions" as a fundament for his "Special Theory of Relativity":
- The law of physics are the same in any frame of reference.
- Space (or SpaceTime) has no preferred "direction", thus we can perform an experiment along the x direction,
or y direction, or any other direction (like the direction where a frame of reference is moving to).
- The speed of "c" in vacuum is totally independent of the speed of any frame of reference.
Einstein further took nothing for granted.
Again, we will consider two frames of Reference, namely S and S'.
S' is moving with speed "v" along the +x direction (when viewed from S), just like in Chapter 1.
As was discussed in Chapter 3, here too we are going to use "events" in Minkowski space, chracterized
by "points" as (x,y,z,ct).
Suppose that at a certain moment, S and S' coincide. Ofcourse, immediately after, S' continue to move
into the +x direction.
Precisely when S and S' coincide, a "light-explosion" from the Origin occurs. The will create a spherical wavefront.
In a completely logical and mathematically correct way, the expanding sperical "wavefront" might be decribed in S as:
Sperical wavefront described from S:
x2 + y2 + z2 = (ct)2 = c2t2 (equation 8).
We can describe the sperical wavefront from the perspective of S' too. Then it will be:
Sperical wavefront described from S':
x'2 + y'2 + z'2 = (ct')2 = c2t'2 (equation 9).
But S' is moving into the +x direction only (as viewed from S). Just like in Chapter 1, there is no reason
to expect "any effect" along the y and z directions. Sure, as you will see in a few minutes,
in the dimension in which we indeed have a "speed" ("x"), we will see a large effect.
But in the transpose directions, thus in this case the directions "y" and "z", there is no effect at all.
It's not fishy. As you will see, a phenomenon as "length contraction" (a relativistic effect) does happen
in the dimension(s) as to which the frames of reference are moving with repect to each other.
In our case, movement is along "x" (or "x'") direction only.
So:
y = y'
z = z' (equations 10-11)
What Einstein actually reallys says, is that an observer in S sees a normal spherical wavefront, but
the same is true for an observer in S'.
This is a direct consequence from the fact that the speed of light is constant, in every frame of reference.
So, not withstanding the fact that S' moves with v into the +x direction, the speed of light will be the same,
so the classical way to add velocity vectors does not hold.
It means that:
x2 + y2 + z2 = (ct)2 = c2t2
x'2 + y'2 + z'2 = (ct')2 = c2t'2 (equations 12-13)
Since the speed that light travels, is the same everywhere, both equations means the same "distance".
If we only have a speed v of S' along the +x dimension, then we can use equations 10,11:
x2 = c2t2
x'2 = c2t'2 (equations 14-15)
or rewritten as:
c2t'2 - x'2 = c2t2 - x2 (equation 16)
Equation 16 forms the basis, to relate x and x', and t and t'
What we really want is a set of relations which expresses x' and t', in terms of x and t, just as we had
with the Galilean transformation (like equations 1-4 of chapter 1).
So, finding those, is our next goal.
There quite a few "variants" of finding the set of relations which expresses x' and t', in terms of x and t.
Although those approaches may seem different, they all ultimately must satisfy equation 16.
The various derivations themselves, consists of some "smart" mathematics, and, I think, it's not really needed to follow
each individual mathematical step in such process.
One constraint on the sought after relations, is that they must converge to the Galilean Transformations when v<<c.
What often is done to find the relations, is expressing x' and t' as linear function of x and t.
-That is mathematically not strange, since equations like equation 16, have linear functions as a solution.
-Secondly, in math in general, the first thing one always try, is the simple linear function, and if that does not work,
then one have to try more complex ones.
-Thirdly, a linear function is a good approximation for more complex functions, if the variances are not large. Then, if it works
out to bee an exact solution, then it's actually not an approximation, but the real solution.
-Fourth, if the relation is not a linear function, there is a physical problem, since quadratic or higher polynimials, or other
functions would give multiple solutions (that is multiple x''s and t's) for the same x and t. That would be truly weird.
So, armed with the four arguments above, we can try:
x' = γx + δt
y' = y
z' = z
t' = εt + ηx (equation 17-20)
Since ultimately at low speeds, the set of equations 17-20 must revert to the Gililean transformations,
we can use that as a check later on, if our solutions found, are indeed valid.
The movement of S' is constant with respect to S, and we are so 'smart' to single out some "special moments"
and use those for further processing of equations 17-20.
It's only a tiny bit "dirty", because I really like to avoid the very lengthy mathematical/algebric processing
which is normally done.
Next to the tactic of to single out some "special moments", we also, we "stronly" suspect that any linesegment
along x', Δx' in S', as seen from S, is contracted.
And, we also "strongly" suspect that clocks in S' run slower, as seen from S.
So, we may say, from a relativistic viewpoint, that it must be that x' = γ x and t' = γ t.
Indeed, we may call "γ" a relativistic factor.
And suppose that we are wrong and there is for example no length contraction, then γ must be "1".
For an observer in S, it still remains a reality that S' moves with speed "v" into the +x direction.
For any precise time "t", at the Origin of S', or the point where x'=0, we have x=vt.
This is just one of those "special moments" I was referring to above.
This leads to:
0 = γx + δt => γ vt = -δ t => γ = -δ/v => δ = - γv.
In this case, we will use "δ = - γv" into "x' = γx + δt" (first equation of the set equations 17-20)
x' = γx -γv t =>
x' = γ (x -vt) (equation 21)
Believe it or not: equation 21 is the first of our 4 sought after Transformation equations.
However, we already also know that y' = y and z' = z, so we are only looking for the time equation. Just one left.
But I don't want to much clutter here, and it's not really neccessary, I think.
If we would persue (quite lot of) more mathematics, we would have found the new transformations to be:
____________________________________________
x'
=
x-vt
-------------
√(1-v2/c2)
y'
=
y
z'
=
z
t'
=
t - (v/c2).x
-------------
√(1-v2/c2)
(equations 22-25)
____________________________________________
If we want, we can simplify the equations above, if we use the "gamma factor" γ, which is:
γ
=
1
-------------
√(1-v2/c2)
(equation 26)
In many articles, however, folks call γ = √(1-v2/c2), and equation 26 "the Lorentz factor".
Since the γ factor (equation 26) is common among the transformation equations,
we may also write (for v along the x-direction):
____________________________________________
x'
=
γ
(x-vt)
y'
=
y
z'
=
z
t'
=
γ
(t - (v/c2).x)
(equations 27-30)
____________________________________________
Equations 22-25, or equations 27-30, the are called the "Lorentz Transformations" (for "v" along the x-direction).
Note that the " γ factor", to a high degree, determines the relativistic effect here.
Take a look at the first equation (22) for x'. Note that if v is ver low, then √(1-v2/c2) is practiclly "1".
Thus it means that the equations converges to the Galilean Transformations for low speeds.
Next, we are going to explore the relativistic effects like "length contraction" and "time dilation".
If "v" is very low compared to "c", then for example the "length contraction" is very low too, or even unnoticable.
However, if "v" is very high, like 0.5c, or 0.7c, the "length contraction" is very considerable.
In principle, you could deduce that from the Lorentz Transformations listed above.
But we are going to play with a few examples in section 4.2.
4.2 "length contraction" and "time dillation":
Length contraction refers to a moving object, which appears to look shorter when viewed in the stationary reference frame.
If it is true that you see this "work" for the first time, I can imagine you will be somewhat amazed.
Again, we have the frames of reference S and S', in the usual way.
In S, we can define a certain "distance" or linesegment Δ x = L0 = (x2 - x1).
Suppose S' was at rest first. Let S' have exactly the same linesegment, which thus completely coincides with Δ x.
At a later moment, we have "placed" S' quite some distance away on the -x direction, and let's suppose S' aquires a high speed,
and further keeps that speed "v" constant, along the +x direction.
At a certain moment, S' will then pass along S, with speed "v". How does an observer in S, measures that linesegment L in S'?
It's actually not so hard to calculate this.
Using the Lorentz transformations, we have:
(x'2 - x'1)
=
γ
(x2-vt)
-
γ
(x1-vt)
=
γ (x2 - x1)
Note how the "vt" terms cancel out.
We have the amazing result that:
Δ x' = γ Δ x.
and:
Δ x = 1/γ Δ x'
We need to get the perspectives right here:
Since γ is always equal to or greater than 1, we see that the length in the stationary frame (the unprimed frame S)
will be equal to or smaller than the length in the moving frame (the primed frame S').
This is a matter of perspective.
If you are "inside" S', thus moving along S', the length is fully normal.
You are inside S' in which the object appears (and is) stationary.
In such a case, you would say that it is the length in S, which is contracted !
γ is always > 1, or almost "1" if the speed "v" is very low.
However, the term "√(1-v2/c2)" is always < 1, or almost nearing (from below) "1",
if the speed "v" is very low.
Length contraction is observed from the stationary frame S, and to be in "effect" in the moving frame S'.
So, always use "Length * √(1-v2/c2)" to get the length of the moving object.
Usually, we write it in the following way.
Suppose L0 is a distance or linesegment in S and S', where both are in rest.
Then if S' moves with speed "v" (relative to S) along the x direction, then an observer in S
measures this segment in S' to have a lenght "L" of:
L = γ L0 where γ=√(1-v2/c2)
Example 1:
Suppose in S, we have L0 = 1m.
When S' is in rest, we have the same distance L = 1m.
Now S' moves with a constant speed of 0.7c along the x direction.
How long does a stationary observer in S, measures L, when S' moves with that speed?
Answer:
L = √(1- 0.7c2/c2) L0 = 0.714 * 1 = 0.714 m
Example 2:
Suppose in S, we have L0 = 1m.
When S' is in rest, we have the same distance L = 1m.
Now S' moves along the x direction with (only) 1000 km/s, which is about 0.003c.
How long does a stationary observer in S, measures L, when S' moves with that speed?
Answer:
L = √(1- 0.003c2/c2) L0 = (practically) √1 * 1 = 1 m
With low speeds, say below 0.01 c, relativistic phenomena are hardly observed.
That's why Newtionian mechanics works great with speeds that are only small fractions of "c".
It's not too hard to try for yourself to how time dilation works.
Indeed, in the moving frame S', a clock will run slower compared to S.
Let's go for our last chapter, on "Causality".
Chapter 5. More about Causality.
It's quite reasonable to say that there (still?) is no "complete" theory in Physics,
which can be used in all domains, that is, from extremely small distances, up to the scale of the Universe.
"Grandfather" theories, like Quantum Mechanics and Relativity, have "follow-up" theories, where physicist
hope that they can (eventually) describe or explain the World even better than those "grand daddy" theories.
I like to talk about "causility" here, since it's also an important theme in STR.
Causality is not limited to physics. All sciences (e.g. history, sociology, medicine, economics etc..) use it in one way
or the other, but it is reasonably fair to say that the β sciences are more involved (including philosophy).
It's difficult to grasp causality. It really is. If you see a phenomenon in physics, then you might
find a "source" which caused that phenomenon. But almost always (if not always), you can investigate
more thoroughly, and find another deeper reason for that cause etc..
For example, you see a force that caused a particle to get in motion, but what caused that force?
Maybe some field? What caused the field .... etc... etc...
You may say: that's not causality! But the stuff above is related.
Some say that causality is directly tied to cause-effect connections, or that it is fully related to
empirical events (possibly repeatable events).
As another example: Some physicist are working on rather strange models (or unexpected models), like "wormholes" on the
scale of the "Length of Planck". In these idea's, causality might have not the usual meaning.
As an example article, you might like to see:
Black Hole as a Wormhole Factory (arxiv)
It's just an example study. There are lots of such studies. Not all physicist would say that it's really
a path that is worth exploring.
Now back to STR. All physicist say that it preserves "causality". Even stronger: the fact that exchange of "information"
is limited to the speed of "c", in all frames of reference, means that one cannot break causality.
Causality means that cause precedes effect. which is an ordering in time which every observer, in all
frames of reference, agrees upon.
However, there are many famous apparent, or possibly real, paradoxes, even when considering scenario's which
does not violate the theory.
SRT SpaceTime diagrams:
Figure 3. Space-Time diagrams
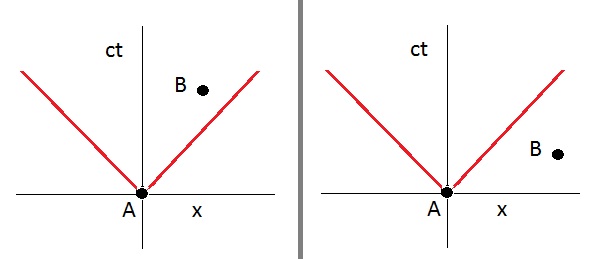
One good tool to check on causality are socalled Space-Time diagrams. In figure 3 you see two examples.
One the x-axis, we see the axis of space (or just one dimension "x").
The y-axis is "ct".
In such scenario, only events between the two red lines (the "cone"), can be causally connected.
The boundary of the "cone", that is, the red lines, represent the distance covered when exactly travelling with "c".
So, within the cone, we are "safe" since any path means that information exchange travels lower than "c",
or at most "c" (on the red lines).
So, if we have two events (two points) A and B, and the path from A to B is within the cone, then never
there was a scenario where information travelled faster than "c". Causality is preserved !
This is depicted by the left figure.
In the right figure, point B is outside the "cone". This means that there is path where information travelled
faster than "c". Causality is broken !
That's it. Hope you liked it !
--
dt'
--
dt'
--
dt'
-------
dt'
--
dt
-------
dt
--
dt
--
dt
-------
dt dt
-----
dt2
Now you start walking in the train, with a speed of 5 m/s in the direction of the front of the train,
then your speed relative to the track (or relative to the surface of the Earth) is 50 m/s + 5 m/s = 55 m/s.
We can simply keep all the examples "one dimensional" here, that is, the speed of an object
is along the direction of a moving frame of reference.
As another example:
Take a look at figure 2 below.
Figure 2. In this example S' is moving in the +x direction with 20 m/s, relative to S.

In this case, an observer in S sees that frame of reference S', is moving with 20 m/s into the +x direction.
So, "everything" in frame S' (including bow and arrow), is moving with that speed, relative to S.
However, since an "abosute" frame of reference does not exist, the observer in S' might simply say that
it is S which is moving into the -x direction with 20 m/s.
Now, suppose the observer in S', shoots an arrow with 30 m/s (relative to S') into the +x direction>
So in S' people would say: the arrow goes with 30 m/s into the +x direction.
But the observer in S measures the speed of the arrow to be 50 m/s. This sum is simply the initial (constant) speed
that the arrow already possesed, and the extra 30 m/s due to the power of the bow.
But this is already we all know what is true. We see it in daily life all the time.
Indeed, in classical mechanics we simply add the speeds, when the object (like the arrow) and the frame of reference
are moving in the same direction.
Now, the startling thing is, that this does not work with ElectroMagnetic radation, like radiowaves, light, x-rays etc..
In this case, such "radiation" travels with "c" (the speed of light), and "c" only.
So, suppose frame S' is moving with 0.7 c with respect to frame S. The observer in S', now fires a laser in the same
direction as S' is moving to.
For observers in S and S', that signal simply has a speed of "c".
So, for an observer in S, the speed of the signal is not 0.7c + 1.0c=1.7c
The speed of "c" (the speed of light) seems to be completely unrelated to the speed of any observer.
This is rather "un-classical".
Let's try to see what scientists did in the past, both on a theoretical and experimental basis, to finally
reach the conclusion that the speed of light is "constant".
Chapter 2. Speed of light.
2.1 A few Experimental observations:
The speed of light in true vacuum, called "c", is just slightly below 300000 km/s (3 * 108 m/s).It is absolutely fenomenal that a Danish astronomer (Romer), already in 1676 determined that the speed is somewhere about 225000 km/s.
He used the eclips of the moon "Io" around Jupiter. The Earth revolves around the Sun in one year ofcourse.
In that orbit, in a period of half a year, we have (so to speak), a near "spot" and far "spot" with respect to
the line of sight with Jupiter.
By comparing the time difference at such eclips, at moments that the Earth is near or far, Romer came to his conclusion.
Note how ingeneous that was.
Ofcourse, at much later years, the speed was determined with increasing accuracy.
Around the mid of the 1800's, Maxwell created a theoretical framework decribing ElectroMagnetic (EM) phenomena in general,
including EM waves.
Somwhere around 1886, Hertz conducted a number of experiments which proved the actual propagation of EM waves
in "free space" (wireless).
Up until the year 1900 (or thereabout), folks still were convinced that ElectroMagnetic radiation (like visible light),
needed a fixed medium, the "ether" (or "aether"), for "propagation".
Indeed, all "waves" observed on a human scale, like the travelling waves in water if you drop a rock in a pond,
are propagating ocillations that use a "medium" for their expansion. Countless of other of such observations exists.
It was quite reasonable in those days, that the same sort of thing must be true for EM waves too.
The "Michelson and Morley" experiments.
One of the first "cracks" in the idea of a fixed "ether", arose with the experiments of Michelson and Morley.
Ironically, those researchers actually did the experiment, with the expectation that it would prove the existence of such an "ether".
If light and other EM radiation, uses a fixed and absolute frame of reference of some substance, called the "ether",
then using an ingeneous experiment might prove it to be true.
Again, it was used that the Earth revolves around the Sun, with an orbital speed of 20 km/s.
Now, in a span of 6 months, the speed of the Earth is opposite than it was 6 months before.
If light travels in an absolute frame, then small differences in the speed of light might be observed, due
to the different speeds of the Earth in 6 months difference.
The experiment was indeed set up in such a way, that differences would be greater than the experimental margins of error.
However, no difference was found !
By the way, in later years the experiment was often repeated, using different setups, with ever increasing accuracy.
In the years close to 1900, it is indeed true that physicists who were involved in this field, we quite puzzled.
Today, countless experiments and observations (including astronomical observations) have been done, and all confirm
that the speed of light is constant, and independent of the speed of the observer.
Note how "un-classical" this is, with respect to traditional classical mechanics.
The "Gedanken" experiment of Einstein.
Einstein passed away in 1955. However, some footage exists where we can hear the master talk.
I forgot a lot of details, but when I was fairly young, a saw a documentary of Einstein,
where he told the viewers of a rather remarkable moment in his early life, way before he published any of his theories.
In a tram, in Bern (Swiss), he watched a clocktower showing a certain time. Einstein then suddenly pondered that the light
of that particular moment, that particular image of the clock, "would be captured", "or frozen" in some way, traveling for ever.
As if time itself was frozen or was halted.
It seems that such event contributes to the early thoughts Einstein had, about Space and time.
While still not so exact as he would formulate it later on, but it seems that already in that tram,
Einstein felt that Space and time are not fully seperate, but connected in "SpaceTime".
As it turned out later on, a "SpaceTime interval" between two events will always has the same "distance",
no matter which frame of reference is used.
Exactly this, will be explained in Chapter 3.
2.2 A few Theoretical considerations:
Transmission of Information:The relevancy that the "speed of light" is the "ultimate speed", and is always the same, independent of the frame of reference,
has "shifted" somewhat, for some scientists, to a (sort of) newer interpretation.
While it still is very true, I think that somewhere around the '70's, the "tone" shifted to that it is
actually the "transmission of information", which cannot exceed the speed of light.
The difference is quite a subtle one. As we will see later, an important thought is that "causality" must be preserved,
and that is also governed by means of how information can be "distributed" (so to speak) among processes and events.
As to how fast an individual "pure sine like" wave travels, is not so relevant: it contains no information.
Information "sits" in how (for example in EM waves) frequencies or amplitudes are modulated in carrier waves.
An individual "harmonic", or pure single wave, among a "group", might theoretically" even go faster than "c".
Before you say that this is an absurd statement, listen to this: some physicist believe that for example in an experimental setup,
where two very long metal sheets are very close, that inside, the amount of quantum fluctuations are somewhat less compared
to the "normal" vacuum (Casimir effect). They argue, on theoretical grounds, that the speed of light then might an extremely small
fraction higher than in regular vacuum c.
But at the same time, it is shown that it does not hold for information transmission.
So, it does not matter at all. Einsteins law is not breached.
Keep in mind that the latter alinea is fully theoretical, and is never tested or proven.
Many physicists also reject such a line of thought, while some still persist in such a view.
But when considering all of this from the perspective of "transmission of information", the case is settled
and done with anyway.
Speed of light in a "medium":
In matter (or a medium), the speed of light is slower than "c". For example, in water
the speed is be only 0.75c (where c is always the speed in vacuum).
In a way, the speed is only apparently lower, since from an "atomic" or "Quantum Mechanical" view,
the photons "collide" with the electrons of the atoms of the material, en gets re-transmitted again.
Overall, that consumes time, and is considered to be a fair explanation, among physicists.
Ofcourse, there is more to say on that, than only the couple of lines above. However, it does not affect
the way we must view "c" in the framework of STR.
The Vacuum:
The "true" speed of light, as the absolute constant, is considered to be in "vacuum".
There are still some "uncertainties" as to what the vacuum exactly is. For example, the concept of "vacuum fluctuations"
where virtual particles "pop up" from the vacuum, and destroy each other again, are considered very seriously in several
disciplines of Physics.
As to "how" this would have any effect on the speed of light, is "really" still not fully covered.
Also, it is generally expected that "c" has to be involved/connected with the fundamental structure of the Vacuum,
or SpaceTime, whether the best theory would turn out to be "superstring theory", or "Loop Quantum Gravity", or something else.
This too is still not fully covered by any theory sofar.
Other fundamental constants which depend (or relate) on (with) c:
Vacuum permittivity of Electric- Magnetic fields:
There is a relation that couples "c" to 2 fundamental electrical and magnetic constants of the Vacuum, namely
ε0 and μ0 which represents the "vacuum permittivity", or "permittivity of free space".
These constants say "something" about the capability/ability of the vacuum to permit electric- and magnetic fields.
| c2 | = |
1 --- ε0 μ0 |
Whether the relation is truly fully exact, still seems to be a subject of debate among physicists.
Also, a correct and fully satisfactory interpretation of the relation, seems to be missing still, although such
a view is not shared by all physicists.
However (in SI units), those constants ε0 and μ0, keep on returning in every fundamental equation of Maxwell's
Theory of Electrodynamics.
A dielectric material, shows a certain permittivity too, which can be related to the polarization or orientation
of charged particles. For the electric field, such a permittivity can then be expressed as ε = εmε0
I am not suggesting that "c" can be exactly calculated from ε0 and μ0, or the other way around.
It's just such an equation that couples constants, and it seems to suggest that a constant "c" is a property of the Vacuum.
I have to confess that I like such discussions, and that is probably the reason why I have put it here.
That probably holds even more for the following subsection.
But you are strongly encouraged (by me) to do some further explorations on this facinating subject.
Planck's Length:
I am not going to say anything here, about the Planck's Length. But I think it will add "something"
to the discussion about the speed of light, why it is always constant, and why it is so important.
If "Planck's Length" really is unknown to you, you might consider to do a websearch, and read some articles.
You won't regret that, I am sure.
If you see the relation which defines the length of Planck and which connects it to fundamental constants, then ask yourself
what possibly the role of "c" can be here.
However, it's not neccessary for this note.
Chapter 3. Minkowski SpaceTime and Distance.
Let's spend a few words on the "Minkovski SpaceTime", since it plays an important role in the approach to STR.But first, let's recapitulate a few properties of "common" vectors (like in R2, R3),
like the "length" or magnitude of an ordinary vector, and the "distance" between points.
3.1 Small Recap on lenghth/distance of vectors in flat Euclidean space:
- The "length" or magnitude of an ordinary vector in a Cartesian coordinate system of a flat Euclidean space:The "magnitude" of vector A is often denoted as |A|, but some other notations go around too.
In a orthonormal Cartesian coordinate system, the calculation of the magnitude is done like in the following examples:
In R2, the length of vector A is |A|=√(x2 + y2)
In R3, the length of vector A is |A|=√(x2 + y2 + z2)
In RN, the length of vector A is |A|=√(x12 + x22 + .. + xN2)
- The "distance" between two points (vectors) in a Cartesian coordinate system:
You can view this stuff in multiple ways. You can say that we "just" have two points P and P', and the line segment
which connects those two points, clearly determines the distance between them.
Or rather equivalent: You can also say that we have a vector P and vector P', and the length of the vector P-P',
simply is the distance to these points defined by P and vector P'.
Some examples:
-In R2:
|PP'|2 = (x2 - x1)2 + (y2 - y1)2
Thus:
|PP'| = √ ( (x2 - x1)2 + (y2 - y1)2) )
-In R3:
For R3, we simply have one additional coordinate. So, we would have:
|PP'|2 = (x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2
Thus:
|PP'| = √ ( (x2 - x1)2 + (y2 - y1)2) + (z2 - z1)2) )
-In Rn:
Suppose we have two points "P" and "Q" in Rn, with the coordinates:
(p1, p2, .. ,pn) and (q1, q2, .. ,qn)
then:
|PQ|2 = (p1 - q1)2 + .. + (pn - qn)2)
Thus:
|PQ| = √ ( (p1 - q1)2 + .. + (pn - qn)2) )
In general, a "distance", is quite often denoted by "S" or "s", or in infinitesemal form "ds".
3.2 Minkowski SpaceTime:
Minkowski SpaceTime is a four-dimensional space, 3 spatial coordinates an one additional time coordinate.You can view it like "just" "another" a four-dimensional space ofcourse, but that's not really the plan.
It is meant specifically to specify events, possibly linked by "lightsignals".
Such an event from a viewpoint of Physics, is for example an observer (or source) sending a lightpulse,
and another observer recieving that lightpulse.
This then would form a connection, or a distance, between those two events (points).
It's that simple.
A point, or event, in Minkowski SpaceTime can be notated as (x1,x2,x3,x4).
However, to give it a better physical interpretation, write it as (x,y,z,ct), since then it is clear that we have indeed
the usual 3 spatial coordinates and one time coordinate.
But why "ct"? Since Minkowski SpaceTime connects events, it's usefull to use "ct", since that defines the standard unit,
that light travels, measured over a standard time, which actually then "functions" as a component distance, just like "x", or "y" etc..
Now, we may have a point, and another point, over which we can easily define a "distance" between those points.
What can be a "reasonable" formulation of a distance in Minkovski SpaceTime? It will have some similarity with
the familiar Euclidean case, but this time the "path" of a lightsignal must be incorperated too.
Let;s try this:
If we have the two events (x1,y1,z1,ct1) and (x2,y2,z2,ct2),
then the ordinary spatial distance would be: √ ( (x2 - x1)2 + (y2 - y1)2) + (z2 - z1)2) )
but that must equal the distance covered by the lightpulse: c(t2 - t1).
This is why often the distance is covered (so to speak) by the equation:
c2(t2 - t1)2 - (x2 - x1)2 - (y2 - y1)2 - (z2 - z1)2 = 0 (equation 7)
Formally, equation 7 is called "the interval", which is "0" in every frame of reference.Equation 7 has some similarities to the "Pythagorean theorem" rewritten as:
c2-a2-b2=0
Based on such ideas, the distance "ds" in Minkowsky SpaceTime can be found to be:ds2=c2dt2-dx2-dy2-dz2 (equation 8)
Actually, this possibly expresses the "core" idea of STR. Since "c" is constant in all moving frames of reference,the Minkowsky distance between events is always the same.
Remember that an event might be viewed as an observer (or source) sending a lightpulse, and another observer recieving that lightpulse.
This distance, between those two events, is the same as viewed from any frame of reference.
So, in Minkowski spacetime, all observers in all frames of reference will agree on the distance in SpaceTime between events.
However, it still needs to be "proven" in a mathematical way, and ofcourse we want to find the equivalent
of the Galilean transformation in this relativistic perspective, like expressing x' in terms of x and t.
As you might already see from equation 8, if a Minkowski distance ds is required to be constant, then in a moving frame of reference S',
a clock must go slower, and some spatial distance (in the direction of motion) must contract, otherwise ds will not
be the same as viewed from frame S. I try to prove that (or better: I try to make it plausible) in Chapter 4.
We are up now for some highlights of the core of STR.
Chapter 4. The core: Lorentz Transformations and STR.
4.1 The relativistic Transformations or the Lorentz Transformations:
Einstein took the following "assumptions" as a fundament for his "Special Theory of Relativity":- The law of physics are the same in any frame of reference.
- Space (or SpaceTime) has no preferred "direction", thus we can perform an experiment along the x direction,
or y direction, or any other direction (like the direction where a frame of reference is moving to). - The speed of "c" in vacuum is totally independent of the speed of any frame of reference.
Einstein further took nothing for granted.
Again, we will consider two frames of Reference, namely S and S'.
S' is moving with speed "v" along the +x direction (when viewed from S), just like in Chapter 1.
As was discussed in Chapter 3, here too we are going to use "events" in Minkowski space, chracterized
by "points" as (x,y,z,ct).
Suppose that at a certain moment, S and S' coincide. Ofcourse, immediately after, S' continue to move
into the +x direction.
Precisely when S and S' coincide, a "light-explosion" from the Origin occurs. The will create a spherical wavefront.
In a completely logical and mathematically correct way, the expanding sperical "wavefront" might be decribed in S as:
Sperical wavefront described from S:
x2 + y2 + z2 = (ct)2 = c2t2 (equation 8).
We can describe the sperical wavefront from the perspective of S' too. Then it will be:Sperical wavefront described from S':
x'2 + y'2 + z'2 = (ct')2 = c2t'2 (equation 9).
But S' is moving into the +x direction only (as viewed from S). Just like in Chapter 1, there is no reasonto expect "any effect" along the y and z directions. Sure, as you will see in a few minutes,
in the dimension in which we indeed have a "speed" ("x"), we will see a large effect.
But in the transpose directions, thus in this case the directions "y" and "z", there is no effect at all.
It's not fishy. As you will see, a phenomenon as "length contraction" (a relativistic effect) does happen
in the dimension(s) as to which the frames of reference are moving with repect to each other.
In our case, movement is along "x" (or "x'") direction only.
So:
y = y'
z = z' (equations 10-11)
What Einstein actually reallys says, is that an observer in S sees a normal spherical wavefront, butthe same is true for an observer in S'.
This is a direct consequence from the fact that the speed of light is constant, in every frame of reference.
So, not withstanding the fact that S' moves with v into the +x direction, the speed of light will be the same,
so the classical way to add velocity vectors does not hold.
It means that:
x2 + y2 + z2 = (ct)2 = c2t2
x'2 + y'2 + z'2 = (ct')2 = c2t'2 (equations 12-13)
Since the speed that light travels, is the same everywhere, both equations means the same "distance".If we only have a speed v of S' along the +x dimension, then we can use equations 10,11:
x2 = c2t2
x'2 = c2t'2 (equations 14-15)
or rewritten as:c2t'2 - x'2 = c2t2 - x2 (equation 16)
Equation 16 forms the basis, to relate x and x', and t and t'What we really want is a set of relations which expresses x' and t', in terms of x and t, just as we had
with the Galilean transformation (like equations 1-4 of chapter 1).
So, finding those, is our next goal.
There quite a few "variants" of finding the set of relations which expresses x' and t', in terms of x and t.
Although those approaches may seem different, they all ultimately must satisfy equation 16.
The various derivations themselves, consists of some "smart" mathematics, and, I think, it's not really needed to follow
each individual mathematical step in such process.
One constraint on the sought after relations, is that they must converge to the Galilean Transformations when v<<c.
What often is done to find the relations, is expressing x' and t' as linear function of x and t.
-That is mathematically not strange, since equations like equation 16, have linear functions as a solution.
-Secondly, in math in general, the first thing one always try, is the simple linear function, and if that does not work,
then one have to try more complex ones.
-Thirdly, a linear function is a good approximation for more complex functions, if the variances are not large. Then, if it works
out to bee an exact solution, then it's actually not an approximation, but the real solution.
-Fourth, if the relation is not a linear function, there is a physical problem, since quadratic or higher polynimials, or other
functions would give multiple solutions (that is multiple x''s and t's) for the same x and t. That would be truly weird.
So, armed with the four arguments above, we can try:
x' = γx + δt
y' = y
z' = z
t' = εt + ηx (equation 17-20)
Since ultimately at low speeds, the set of equations 17-20 must revert to the Gililean transformations,
we can use that as a check later on, if our solutions found, are indeed valid.
The movement of S' is constant with respect to S, and we are so 'smart' to single out some "special moments"
and use those for further processing of equations 17-20.
It's only a tiny bit "dirty", because I really like to avoid the very lengthy mathematical/algebric processing
which is normally done.
Next to the tactic of to single out some "special moments", we also, we "stronly" suspect that any linesegment
along x', Δx' in S', as seen from S, is contracted.
And, we also "strongly" suspect that clocks in S' run slower, as seen from S.
So, we may say, from a relativistic viewpoint, that it must be that x' = γ x and t' = γ t.
Indeed, we may call "γ" a relativistic factor.
And suppose that we are wrong and there is for example no length contraction, then γ must be "1".
For an observer in S, it still remains a reality that S' moves with speed "v" into the +x direction.
For any precise time "t", at the Origin of S', or the point where x'=0, we have x=vt. This is just one of those "special moments" I was referring to above.
This leads to:
0 = γx + δt => γ vt = -δ t => γ = -δ/v => δ = - γv.
In this case, we will use "δ = - γv" into "x' = γx + δt" (first equation of the set equations 17-20) x' = γx -γv t =>
x' = γ (x -vt) (equation 21)
Believe it or not: equation 21 is the first of our 4 sought after Transformation equations.However, we already also know that y' = y and z' = z, so we are only looking for the time equation. Just one left.
But I don't want to much clutter here, and it's not really neccessary, I think.
If we would persue (quite lot of) more mathematics, we would have found the new transformations to be:
____________________________________________
| x' | = | x-vt ------------- √(1-v2/c2) |
| y' | = | y |
| z' | = | z |
| t' | = | t - (v/c2).x ------------- √(1-v2/c2) |
(equations 22-25) |
If we want, we can simplify the equations above, if we use the "gamma factor" γ, which is:
| γ | = | 1 ------------- √(1-v2/c2) |
(equation 26) |
In many articles, however, folks call γ = √(1-v2/c2), and equation 26 "the Lorentz factor".
Since the γ factor (equation 26) is common among the transformation equations,
we may also write (for v along the x-direction):
____________________________________________
| x' | = | γ | (x-vt) |
| y' | = | y |
| z' | = | z |
| t' | = | γ | (t - (v/c2).x) |
(equations 27-30) |
Equations 22-25, or equations 27-30, the are called the "Lorentz Transformations" (for "v" along the x-direction).
Note that the " γ factor", to a high degree, determines the relativistic effect here.
Take a look at the first equation (22) for x'. Note that if v is ver low, then √(1-v2/c2) is practiclly "1".
Thus it means that the equations converges to the Galilean Transformations for low speeds.
Next, we are going to explore the relativistic effects like "length contraction" and "time dilation".
If "v" is very low compared to "c", then for example the "length contraction" is very low too, or even unnoticable.
However, if "v" is very high, like 0.5c, or 0.7c, the "length contraction" is very considerable.
In principle, you could deduce that from the Lorentz Transformations listed above.
But we are going to play with a few examples in section 4.2.
4.2 "length contraction" and "time dillation":
Length contraction refers to a moving object, which appears to look shorter when viewed in the stationary reference frame.If it is true that you see this "work" for the first time, I can imagine you will be somewhat amazed.
Again, we have the frames of reference S and S', in the usual way.
In S, we can define a certain "distance" or linesegment Δ x = L0 = (x2 - x1).
Suppose S' was at rest first. Let S' have exactly the same linesegment, which thus completely coincides with Δ x.
At a later moment, we have "placed" S' quite some distance away on the -x direction, and let's suppose S' aquires a high speed,
and further keeps that speed "v" constant, along the +x direction.
At a certain moment, S' will then pass along S, with speed "v". How does an observer in S, measures that linesegment L in S'?
It's actually not so hard to calculate this.
Using the Lorentz transformations, we have:
| (x'2 - x'1) | = | γ | (x2-vt) | - | γ | (x1-vt) | = | γ (x2 - x1) |
Note how the "vt" terms cancel out.
We have the amazing result that:
Δ x' = γ Δ x.
and:
Δ x = 1/γ Δ x'
We need to get the perspectives right here:
Since γ is always equal to or greater than 1, we see that the length in the stationary frame (the unprimed frame S)
will be equal to or smaller than the length in the moving frame (the primed frame S').
This is a matter of perspective.
If you are "inside" S', thus moving along S', the length is fully normal.
You are inside S' in which the object appears (and is) stationary.
In such a case, you would say that it is the length in S, which is contracted !
γ is always > 1, or almost "1" if the speed "v" is very low.
However, the term "√(1-v2/c2)" is always < 1, or almost nearing (from below) "1",
if the speed "v" is very low.
Length contraction is observed from the stationary frame S, and to be in "effect" in the moving frame S'.
So, always use "Length * √(1-v2/c2)" to get the length of the moving object.
Usually, we write it in the following way.
Suppose L0 is a distance or linesegment in S and S', where both are in rest.
Then if S' moves with speed "v" (relative to S) along the x direction, then an observer in S
measures this segment in S' to have a lenght "L" of:
L = γ L0 where γ=√(1-v2/c2)
Example 1:Suppose in S, we have L0 = 1m.
When S' is in rest, we have the same distance L = 1m.
Now S' moves with a constant speed of 0.7c along the x direction.
How long does a stationary observer in S, measures L, when S' moves with that speed?
Answer:
L = √(1- 0.7c2/c2) L0 = 0.714 * 1 = 0.714 m
Example 2:
Suppose in S, we have L0 = 1m.
When S' is in rest, we have the same distance L = 1m.
Now S' moves along the x direction with (only) 1000 km/s, which is about 0.003c.
How long does a stationary observer in S, measures L, when S' moves with that speed?
Answer:
L = √(1- 0.003c2/c2) L0 = (practically) √1 * 1 = 1 m
With low speeds, say below 0.01 c, relativistic phenomena are hardly observed.
That's why Newtionian mechanics works great with speeds that are only small fractions of "c".
It's not too hard to try for yourself to how time dilation works.
Indeed, in the moving frame S', a clock will run slower compared to S.
Let's go for our last chapter, on "Causality".
Chapter 5. More about Causality.
It's quite reasonable to say that there (still?) is no "complete" theory in Physics,which can be used in all domains, that is, from extremely small distances, up to the scale of the Universe.
"Grandfather" theories, like Quantum Mechanics and Relativity, have "follow-up" theories, where physicist
hope that they can (eventually) describe or explain the World even better than those "grand daddy" theories.
I like to talk about "causility" here, since it's also an important theme in STR.
Causality is not limited to physics. All sciences (e.g. history, sociology, medicine, economics etc..) use it in one way
or the other, but it is reasonably fair to say that the β sciences are more involved (including philosophy).
It's difficult to grasp causality. It really is. If you see a phenomenon in physics, then you might
find a "source" which caused that phenomenon. But almost always (if not always), you can investigate
more thoroughly, and find another deeper reason for that cause etc..
For example, you see a force that caused a particle to get in motion, but what caused that force?
Maybe some field? What caused the field .... etc... etc...
You may say: that's not causality! But the stuff above is related.
Some say that causality is directly tied to cause-effect connections, or that it is fully related to
empirical events (possibly repeatable events).
As another example: Some physicist are working on rather strange models (or unexpected models), like "wormholes" on the
scale of the "Length of Planck". In these idea's, causality might have not the usual meaning.
As an example article, you might like to see:
Black Hole as a Wormhole Factory (arxiv)
It's just an example study. There are lots of such studies. Not all physicist would say that it's really
a path that is worth exploring.
Now back to STR. All physicist say that it preserves "causality". Even stronger: the fact that exchange of "information"
is limited to the speed of "c", in all frames of reference, means that one cannot break causality.
Causality means that cause precedes effect. which is an ordering in time which every observer, in all
frames of reference, agrees upon.
However, there are many famous apparent, or possibly real, paradoxes, even when considering scenario's which
does not violate the theory.
SRT SpaceTime diagrams:
Figure 3. Space-Time diagrams

One good tool to check on causality are socalled Space-Time diagrams. In figure 3 you see two examples.
One the x-axis, we see the axis of space (or just one dimension "x").
The y-axis is "ct".
In such scenario, only events between the two red lines (the "cone"), can be causally connected.
The boundary of the "cone", that is, the red lines, represent the distance covered when exactly travelling with "c".
So, within the cone, we are "safe" since any path means that information exchange travels lower than "c",
or at most "c" (on the red lines).
So, if we have two events (two points) A and B, and the path from A to B is within the cone, then never
there was a scenario where information travelled faster than "c". Causality is preserved !
This is depicted by the left figure.
In the right figure, point B is outside the "cone". This means that there is path where information travelled
faster than "c". Causality is broken !