Astronomy/Cosmology
(R: ready, D: in development)
Remarkable events or observations
(R: ready, D: in development)
My simple notes on Math:
(R: ready, D: in development)
Short and simple Database notes:
(R: ready, D: in development)
(It's all a bit old)
Very Simple notes on Defense
(R: ready, D: in development)
My simple notes on Physics:
(R: ready, D: in development)
My simple notes on Astronomy:
(R: ready, D: in development)
My simple notes on Ransomware:
(R: ready, D: in development)
Listing of exploits and CVE's:
My simple notes on Repair Operating Systems
(R: ready, D: in development)
Simple notes on modern ideas on
SpaceTime and Matter.
(R: ready, D: in development)
My simple IT notes:
(Some are a bit old, sorry).
(R: ready, D: in development)
My Simple Programming notes:
(R: ready, D: in development)
Other documents:
-Fun stuff:
-Other IT:
-Great Animals (Present and Past):
-Dutch/Nederlands:
-Other:
About my site.
-My tips:
-Baboon Albert:
A few simple words on Nuclear weapons.
Date: 3 July, 2019Version: 4.3
Remark: Almost ready.

Photo: WikiMedia commons.
"Trinity", the very first nuclear explosion (test), on July 16, 1945, in a desert, New Mexico (USA).
The photo shows the explosion just 0.016 sec (16 ms) after detonation.
The explosion was estimated to be of a magnitude of 15 - 22 KiloTon. In the figure, the diameter of the
ball is about 210 m at that point in time.
The device was "pure fission", mainly based on Pu, using the "implosion" technique.
It was in fact a small device, compared to the "hundreds of KiloTon", or "MegaTon", classes of weapons.
Only a smaller percentage of the total amount of fissable material, actually fissioned at the "Trinity" test.
It is known fact, that with Fatman (the third nuclear explosion ever), from the about 6 kg Pu,
only about 1 kg actually fissioned.
My main objective is to try to "quantify/qualify" modern operational devices, which
might help an individual to realize that, presently, we have a truly dangerous situation.
We have no other choice than (to try) to halt the current developments, and work our
way back to reasonable Treaties again.
It would be unwise to put politically loaded comments in such text. I really like to avoid that
as much as possible, but I found out, that it is not completely unavoidable.
Ofcourse, I have a completely insignificant website. Indeed: who reads this anyway?
This is a very simple note on nuclear devices, viewed from a rather "wide" angle, so I believe.
It's much better that the World gets freed from nuclear devices. At least, the number should
be significantly lowered. However, I am afraid the opposite is true.
Research is still rather intense. Some nations are increasing their operational- and stockpiled weapons.
As another thing, the last years we can see an increase in power of some weapons, development in stealth,
and other developments like hypersonic cruise missiles, capable of carrying a nuclear warhead.
On the onther hand, downsizing of nuclear devices is a fact, since a long time by now,
e.g. mounts in cruise missiles goes back decades ago.
However, further downsizing (in energy output) is extremely dangerous, since the treshold
of actually deploying such weapons, is very low.
Many delivery systems in general, are not "cancelable" (no "undo"), meaning "once fired",
well..., I think you know.
Maybe a simple note, as this one, can help to establish a better idea on the present situation,
and what exactly we are talking about.
However, it could be too simple to have any effect. If so, then I am really sorry for that.
Anyway, I hope that a "mere" abstract and simple view as "Some bunch of some rockets somewhere...",
will turn into a more accurate view of undestanding some basics of the technology and a better understanding
of the actual machinery and devices in operation today.
Apart from phenomena like Aggression, Stupidity, Small conflicts that escalate, Accidents,
Misunderstandings etc.. etc.., which all could lead to the use of nuclear weapons,
other, possibly slightly less known physical factors may play a role too.
First you must know that some nuclear systems are "autonomous" like the infamous "Dead Hand"
launching system. Here too, severe mistakes may occur. Ofcourse, we can think of all sorts
of reasons why it may go wrong. But, here I will launch a rather lesser known, and maybe even
surprising possible cause, of where it all may go wrong.
For example, do you know of the "Carrington event" which happened in 1859?
If not, then look it up. Such events are not "very rare" at all.
And then imagine what could be the implications for modern society.
Apart from severe malfunctions of all electrical systems all over the World, even nuclear Reactor
meltdowns are by no means unthinkable. Also, unintended launches might then occur too, especially
by autonomous systems. Fantasy? I think not.
Contents at a glance:
1. Quick and simple overview of Nuclear weapons.
2. A few words on Generations of Nuclear weapons.
3. The basic principles of fission and fusion.
4. The basic principles of the pure Fission- and Thermonuclear devices.
5. Overview Nuclear capabilities per Nation.
5.1 Unclearity about counts of devices.
5.2 Main current nuclear weapons of Russia.
5.2.1 Introduction
5.2.2 Current ICBM's (landbased,)
5.2.3 Current Strategic bombers
5.2.4 Current SLBM's and nuclear submarines
5.2.5 Current nuclear capable Cruise missiles
5.2.6 Supplies of fissile materials and imports/exports
5.3 Main current nuclear weapons of France.
5.4 Main current nuclear weapons of Great Britain (UK).
5.5 Main current nuclear weapons of India and Pakistan.
5.5.1 Main nuclear weapons of Pakistan.
5.5.2 Main nuclear weapons of India.
5.6 An attempt to say something on the Nuclear capabilities of NK.
5.7 Main current nuclear weapons of China.
5.8 Main current nuclear weapons of the USA and NATO.
Appendix 1: Materials in Nuclear Technologies.
Beryllium.
Lithium.
Uranium.
Plutonium.
Quick overview Reactors.
Control, and exports/imports fissile materials.
1. Quick and simple overview of Nuclear weapons.
I personally like to talk on "generations" of nuclear weapons, as will be shownas of chapter 2 below.
I think it helps to understand slightly better, where something like a neutron bomb must be placed.
However, many folks catagerorize nuclear weapons (somewhat generalized) in the following "types"
as shown directly below. Therefore, it is important to start showing this generalized listing first:
1.1 Generalized classification of types:
- A "pure fission" weapon. It obviously uses "fission" only. The "fuel" might be 239Pu
or 235U. The very first bombs were pure fission weapons.
The isotopes mentioned above, are "fissile" and are capable to undergo a fast chainreaction of fission
of the nuclei, if certain conditions are met (geometry, density etc..), after an initial neutron flux. - A "boosted" fission weapon. A pure fission weapon can be boosted by layers of Tritium and Deuterium,
or compounds as Lithium6-Deuteride.
Or, a central sperical region contains small amounts of Tritium and Deuterium, or compounds as
Lithium6-Deuteride, or other "stuff", that is capable to extremely fast release Tritium or Deuterium,
under neutron bombardment.
The outer shell of the "boosted" weapon, then has a similar architecture as the pure fission type.
The main "gain" by using a small amount of such light elements, is that they increase the amount
(or percentage) of "fission" of 239Pu, and thus strongly increase the efficiency
of the fission bomb. In effect: from all fissile material, a larger percentage will actually fission.
This also provided for possible downsizing of the device, due to the increase of efficiency.
As we will also see later on, this is due to a large neutron generation of those light elements.
This class is often not considered to fall into the real thermonuclear "multi-stage" weapons.
But most folks do say these are thermonuclear weapons. - The Thermonuclear weapons (H-bomb class). These are multi-stage weapons (often two stage),
with a primary fission stage (of heavy nuclei), and a secondary stage which often combines fission and fusion,
where usually, in that second stage, fusion (of light nuclei) is the main contributor to the
energy output of the detonation.
To get an overall impression, you might want to take a look at the figures 5, 6, and 7 below.
A popular name for the "real" Thermonuclear device, is "hydrogen bomb".
Still, those too, are often referred to as "Thermonuclear weapons".
The principles behind nuclear "fission" and "fusion" will be explained in chapter 3.
However, in a nutshell:
-The nuclei of heavy fissile isotopes such as 239Pu, after a neutron capture, may break up, or fission,
into two lighter isotopes. In this process, a large amount of energy is released, as well as other neutrons
(2 or 3) are released.
If almost all nuclei of all atoms of, say, 5 kg of 239Pu or 235U, do that (more or less) at
"almost" the same time (fast sequence of generations of chainreactions), an extremely fast and enormous powerful
detonation follows.
To trigger the "fission" of subcritical parts of 239Pu or 235U, those parts are
often spherically arrangend into a "core" structure. An outer shell, after an conventional explosion,
will quickly compress the subparts into a much more compact mass, where then fission may start to occur.
An initial neutron flux might be required too, to sufficiently startup the rate of fission at start.
An important issue at design of pure fission weapons, is the layout of the conventional explosives
in the outer shell, and the critical timing issues involved, to ensure a smooth compression of the
geometrical object containing the fissile material.
Those timing issues are in the range of about 10 nanoseconds, to ensure an adequate shockwave
for a symmetrical compression of the subcritical fissile parts. This makes the implementation of even relatively simple
fission weapons, very hard. Indeed, many countries struggled with such issues at first, and the very first
devices were "fizzles", meaning that only a fraction of the material actually fissioned.
In such case, we have a "failed bomb", with a relatively low yield.
The very first nuclear weapons worked solely by that principle. These are "pure fission" weapons.
-The nuclei of very light isotopes, such as Deuterium or Tritium, may "melt", or fusion, into a somewhat more
heavier isotope like a Helium nucleus. Also, in this process, are large amount of energy is released.
Thus, if a relatively large amount of such isotopes all "melt", or fusion, more or less at the same time,
an extremely fast and enormous powerful detonation follows.
For fusion to start, a high pressure and Temperature is needed. That's why this process is often started by
using a "pure fission" stage (actually a fission bomb).
1.2 Types of delivery:
Having nuclear weapons is one thing. How to "deliver" them, is another.Larger nuclear nations potentially have, generally speaking, the following options:
Tactical weapons / methodology:
Often shorter distances are involved, like with using Jets, or using smaller, shorter-range rockets.The methodology can also be associated with battle fronts, and local area's.
Strategic weapons / methodology:
Often larger distances are involved, using:- Large ICBM's (Inter Continental Ballistic Missiles), which might be launched from stationary silo's,
or from specialized heavy trucks.
It's not uncommon that their range is well over 10000 km, have a max speed of around mach 8 - mach 22,
and reach their targets within 30 min. - SLBM's (Submarine Launched Ballistic Missiles), which in principle can be fired from "anywhere".
Having a medium- to long range, will type these rockets too.
Many ballistic missiles (ICBM, SLBM) are setup in MIRV (Multiple Independently targetable Reentry Vehicle) configuration.
That is, the "payload" of the ballistic missile consists of multiple independent warheads.
Typical examples of the numbers of warheads is 3, 5, 6, or 10 (or even more).
One main reason for deploying MIRV, is to counteract ABM, or "anti-ballistic" missile defense systems.
The MIRV setup might enable to "release" the individual warheads in slightly different trajectories,
and locate targets which might be several hundreds of km apart. - Strategic bombers: long-range bomber planes.
Here you might think of dropping gravity bombs (drop and fall), but launching sub-, super-, and hyper sonic
nuclear cruisemissiles from a bomber, is getting increasingly "popular" too.
A trend exist, to enable the member warheads to have "maneuverable re-entry" capabilities
in order to make interception even harder, and in fact, almost practically impossible.
Examples hereof, are the Russian RS-28 Sarmat, RS-24 Yars, and the Chinese DongFeng DF-41.
Most large nuclear capable nations use such a "triade" of deterrence, or are striving to realize it.
Note:
There is no very strict seperation between Strategic- and Tactical methodologies.
A max range of 300km is obviously for "local" use, and 13000km is obviously typed as stratigic.
However, quite a few medium ranges for delivery systems "sits in between".
Note:
Again with respect to distances: For many types of nuclear capable missiles, often a classification
like the following can be used. Do not take the ranges in km as too strickt.
-SRBM: Short Range Ballistic Missile (often so called, if range < 1000km).
-MRBM or IRBM: Medium Range Ballistic Missile, or Intermediate-range Ballistic Missile (if range < 3500km).
-ICBM's or SLBM's. (Typed as ICBM if range > 5500km).
-Cruise Missiles, which usually have a short range, to medium range capacity.
Especially, the hypersonic (> mach 5) nuclear capable, cruise missiles, are considered to be a new threat.
This threat is even increased by the implementation of "evasion" techniques and implementation
of non predictive trajectories.
Here is a nice YouTube vid, saying something useful on how to stop ICBM's, and other info.
How can you stop a Nuclear Missile?
1.3 Increase in Nuclear capabilities:
Regrettably, the last few years, we have seen an increase in nuclear capabilities.Here, I do not refer to North Korea (NK), since their capabilities are still rather limited.
Although the situation in that region, has the potential to trigger a larger scale confrontation.
That's really dangerous.
Fortunately, there is some relaxation between SK and NK right now, and hopefully that will
continue, towards still better results....
Hopefully, Pres. Trump will also keep a relaxed attitude here.
The increase in nuclear capabilities, as I see it, can be largely attributed to the Russian Federation.
I really regret to say that, since I do not want something to sound as if it is "politically coloured".
However, for example, their large RS-28 Sarmat ICMB (see chapter 5), planned for operational status 2018 - 2019,
is a weapon with an absurd over-capacity.
The "Avangard" warhead gliding (evasion) technology is implemented with the Sarmat.
Also, the missile lends itself for certain selected mixtures of large- and smaller warheads.
It's seriously believed that up to 20 warheads might be the payload, or a smaller number of *really*
heavy nuclear devices.
As another thing: what about the real status of their nuclear torpedo "Status-6" (Kanyon).
Is it really "real"? This device is much like a submerged ICBM, also with respect to the large range it can cover,
supposedly many thousends of km, with a warhead > 1Megaton.
After serious study, I can tell you that such sort of devices are indeed absolutely real.
Also, the increase in deployment of medium range nuclear rockets, near Europe,
cannot be taken lightly either. For example, you might study the RS-26 Rubezh, and simply conclude
that Europe is a "natural" target for that device. To me, it looks somewhat like an INF treaty breach.
Indeed, also the latest generations (of certain types) of their hypersonic cruise missiles, can be loaded
with nuclear devices, and are generally regarded as "unstoppable".
Furthermore, for example, the nuclear aspiration of India, is also simply huge.
Their development in ballistic missiles is intense, and also they have the first of a series
of nuclear subs operational, namely the "INS Arihant" in the Arihant class.
These vessels will probably be equipped with the K4 SLBM's.
Unfortunately, constant tensions existed between Pakistan and India, since 1947, and up to this very day.
Apart from territory claims, another serious reason became stronger and stronger: Water resources.
This must be taken very seriously, and you might want to study the ever increasing water conflicts
between both states.
Generally speaking, the "increases in nuclear capabilities" Worldwide, is rather large, and treaties are lacking,
and/or practically not in effect anymore.
I will absolutely try to filter out any politically coloured statements from this text.
But to identify countries with their capabilities, is a fundamental theme of this note.
This is the subject of chapter 5.
1.4 Why is Energy output of a nuclear device so high?
"Chemical energy" versus "Nuclear energy".
In just a few words...:Chemical energy:
It's certainly not easy to describe chemical energy, or for that matter, describe nuclear energy.
Many factors play a role here.
For example, when studying molecules, one need to take into account many terms like
potential energies, vibrational and rotational energies etc..
However, I can focus on a few important components, thanks to the simple atom model of Rutherford / Bohr.
It can help to see why nuclear processes may yield more energy.
When considering just some "atom" of a certain element, we can describe the energy levels of the electrons,
(in the "outer shells"), and compare it to the binding energies of the protons/neutrons inside the nucleus.
Please realize that the simple atom model of Rutherford/Bohr is not fully consistent with Quantum Mechanics (QM),
or not even with classical theories. For example, "well-defined" positions of electrons are not consistent with QM.
However, the "shells" correspond nicely with an abstract representation of the discrete "energy levels",
which makes the model indeed rather usable.
Captured in "energy levels", some typical energies for an electron to change shells, or to get free, sits in the
order of tens of eV, or hundreds of eV, to a maximum of some thousends of eV etc...
This is an important component of "capturing"/"visualizing" chemical energy.
Note: the "electronVolt" (eV) is a convienient and standard energy measure to describe energies in the
in the atomic domain, or elementary particles.
Nuclear energy:
Typical binding energies of protons/neutrons in the atomic nucleus, sits in the ranges of many MeV (mega eV).
This is an important component of "capturing" nuclear energy.
This maybe a nice pointer that typical nuclear processes (per Atom), are much more "energetic" than
chemical processes.
So, typically, certain nuclear processes deliver a factor of several thousends more energy, compared
to chemical energy output "per atom".
It's very instructive to take a look at the figure below.
Fig. 1: Average binding energy per nucleon (proton or neutron), against the mass number (the elements)
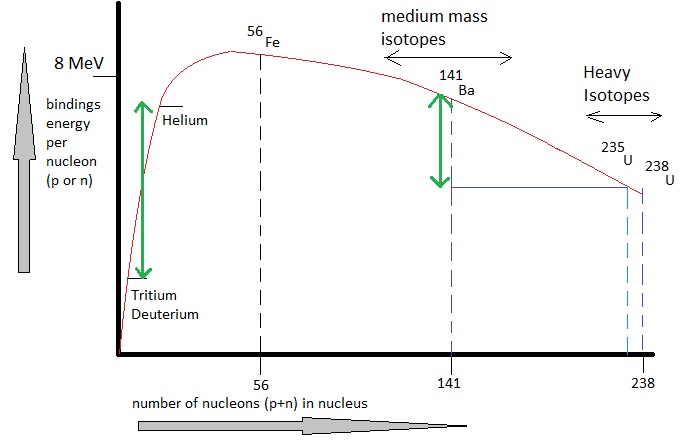
Source: My own Jip Janneke figure, as an approximation of experimental graphs from Physics.
So, a socalled "fissile" heavy isotope as 235U, may split up (after capture of a single neutron),
in two medium weight isotopes (like Ba).
If you look at the figure, the energy difference per nucleon (proton or neutron) is in the order of a couple of MeV.
So, if one whole 235U atomic nucleus splits up (while containing 235 protons/neutrons), the whole
energy difference then is in the order of 200 MeV (per atomic nucleus).
So, if you would have 1 kg of fissile Uranium or Plutonium, and you would manage (in some way) that all
nuclei splits in more or less the same time, you have an equivalent of many thousends of explosive power
compared to 1kg of the best chemically based bombs.
Some fissile heavy isotopes like 235U or 239Pu, have the chacteristic that when
a certain "mass/concentration/geometry" is reached, together with an initial flux of neutrons, will participate
in very fast generations of chainreactions of fission.
The story above is actually way too simple, and a more thourough explanation will follow in chapter 3.
1.5 Some principal "explosive" materials in nuclear devices.
1. 239Pu (Plutonium), 235U (Uranium):For "pure fission", most often the heavy isotopes 239Pu (Plutonium), or 235U (Uranium) is used.
Those "fissile" isotopes have the property to be able to absorb a (slow or fast) neutron, then to break up
into medium weight isotopes (like Ba), while releasing a large amount of energy, and a few fast neutrons too.
Under the right circumstances, it's possible that a supercritical amount displays the fact of fast chainreactions,
meaning that in an uncontrolled way, one fission "ignites" other fissions (due to the released neutrons of the former fission),
faster and faster (almost exponentially).
So, 239Pu (Plutonium) or 235U (Uranium), can function as the primary fissile isotope
of the active core.
2. 238U (Uranium):
The most abundand isotope of Uranium, that is 238U, does not display (in the sense discussed above),
the fact of fast sequences of chainreactions.
However, it can still fission (break-up) like the isotopes described above do.
-"fissile" is often described as the capability to fission with fast neutrons, and slow (thermal) neutrons.
-"fissionable" is often described as the capability to fission with fast neutrons only.
But more often, people understand "fissile" to be the property that the neutrons emitted during fission
of a nucleus, can cause other nuclei to fission as well. Under the right circumstances, it could lead
to fast chain reactions.
U235 is fissile, while U238 is not, But U238 is "fissionable", and it will fission with the use of
fast neutrons (> 1 MeV).
238U can even play an important part in the energy output of a nuclear device.
Suppose you have an outer spherical, or cilindrical "tamper" (casing) of 238U, surrounding
a nuclear device. At detonation, a large flux of high energetic neutrons bombard the tamper, resulting
in a considerable amount of fission of 238U, and thus a considerable contribution
in the total energy output is realized.
The tamper is also designed to "hold" the (core) Plutonium fission fast chain reactions, just to give it
"more time" to exponentially increase fast chain-reactions in the core.
The real active core device uses 239Pu (Plutonium) or 235U (Uranium), but once fission of
those isotopes reach the detonation point, due to a large neutron flux, "some" fission of such outer mantel
starts as well.
However, 238U itself cannot support a chain reaction, which is indeed the property of 235U.
It is indeed true that 238U is "fertile" and can mutate in 239Pu under neutron flux.
However, the latter is not responsible for the larger part of the energy contribution from 238U.
Lastly, next to the tamper fuction (structural support), it also, to a certain amount, scatters neutrons
back to the core, which will contribute to the chain reactions in the core.
The fact that common 238U may contribute in a nuclear device, might have surprised you!
3. 233U (Uranium isotope U233):
This isotope can only be expected to be detected as a "trace" in Nature.
U233 can be produced (after various subreactions) by neutron capture of Thorium-232.
It is fissile too, meaning that it "could" be regarded as a fuel for a nuclear device.
However, it is extremely difficult to handle. Also, due to nuclear reactions, there exist
a certain level of highly active U232 contamination in U233.
It is known that only a few experimental nuclear weapons have been tested, where U233
was used in some combination with U235 or Pu239 (e.g. operation Teapot, around 1955).
It is indeed true, that on average U233 produces about 15% more neutrons per fission, compared
to U235 or Pu239. Still, U233 may be regarded as a less common fuel for nuclear devices.
It may also, get more and more attention for newer generation of (Thorium based) nuclear plants.
So, two fissile isotopes of Uranium exist: U235 and U233. U235 can be found in nature,
in small abundances (0.7%), but it can be enriched (increasing the % level of U235, in Uranium).
Contrary, U233 is "bred" from Thorium.
4. Tritium 3H, and Deuterium 2H:
This is the most common form of fusion. These very light elements might "melt" into (e.g.) Helium, where energy is
released at such event. This is "fusion" (somewhat the opposite of fission).
The most common fusion partners are the Hydrogen isotopes Tritium and Deuterium.
Since Tritium has a "half-live" of about 12 years, in practice, often some compound containing Lithium-Deuteride
is used, which can extremely rapid release Tritium (by nuclear reaction), thereby avoiding the problem
of the natural decay of tritium.
5. Deuterium - Deuterium:
In principle Deuterium - Deuterium fusion can be used, however, the initially required Temperature
is higher, and this is why it is not used in Thermonuclear devices.
6. Lithium 6/7:
Deuterium-Tritium fusion is the most common form of fusion, attainable on our Planet. In e.g. Stars,
other fusion processes are possible too. However, in fusion reactors, physicists try research any
form of usable fusion process, like with Deuterium-Deuterium.
However, using both lithium-6 and lithium-7 will contribute to the fusion reactions and neutron production.
First, indeed both will produce additional Tritium in a extremely fast manner, contributing to the regular
Deuterium-Tritium fusion. Also, a high flux of energetic neutrons will be produced in the nuclear reactions
involving Lithium, which will contribute too in the overall fusion process (and in the optional
fissionable mantle surrounding the device).
2. A few words on Generations of Nuclear weapons.
2.1 The 1st, the 2nd and 3rd generations.
2.1.1. The 1st and 2nd generations.
Although some idea's on nuclear bombs already existed, early in the former century (e.g. H.G Wells, 1914),it all became much more serious shortly before the start of WWII (around '39 of the former century).
As we all know, the first "pure fission" weapons (A-bomb) were developed in '44/'45, and two of them
were actually really dropped on two Japanese cities. Due to immense respect of the victims, I dare not say anything
about the "socalled" neccessity as to why they were really used, but it resulted in an absolute, complete total horror.
Then, in the early '50's. the first "thermonuclear" devices were tested.
In a way, you might call the thermonuclear device, a multi-stage weapon.
The thermonuclear class are "multi-stage" weapons, and very often just "two-stage" devices.
The primary stage then, uses pure "fission", like for example with a implosion technique Pu weapon.
The secondary stage is charcterized with materials which can "fuse", like Tritium with Deuterium, or a compound
as "Litium6 Deuteride", or another suitable substance.
The processes behind "fission" and "fusion" will be explained later (chapter 3).
When the primary stage detonates, within µ seconds, the energy and radiation is so intense, that it will sufficiently heat up
the secondary stage, where primarily "fusion" takes place.
So, this weapon might also be typed as a "fission-fusion" weapon.
In certain cases, the stages, or the entire weapon, might be enclosed by a fissionable 238U, which will
fission too (due to an intense neutron flux), when the secondary stage is detonating.
However, today, a true "pure" fusion weapon does not exist yet. There is always (up to now) a first "fission component".
Some people call the devices above, the "first"- and "second" generation.
Today, the "thermonuclear" device (in all sorts and shapes) is the most abundant type of weapon.
They can be used in tactical situations (the accent here is "local regions"), or strategic deployments
(the accent here is on long distance, like in rather large ICBM rockets, or long range bombers).
A popular name for the "thermonuclear" device, is the "Hydrogen bomb" (referring to the fusion stage, using
Hydrogen isotopes).
Since the very early designs, during the '50s and '60s, downsizing of both fission and fission/fusion weapons
was realized. Using neutron reflecting materials, optimizing geometry, increase in efficiency, made that possible.
But especially, by adding Tritium and Deuterium, it was feasable to greatly enhance the efficiency of "fission",
and it became possible to "downsize" weapons while still having a large blast. Indeed, the "boosted fission" weapon
became more easily to mount in rockets. This still holds for present times.
This is also a reason why "boosted fission" weapons are counted as "thermonuclear" devices.
But it's essentially the high increase efficiency of "fission" of the 239Pu (Plutonium), 235U (Uranium)
primary payload, which explains the term "boosted fission" weapon (due to amounts of Tritium and Deuterium,
and/or Lithium).
If we take a deeper look into the true multi-stage thermonuclear weapon, we know that the primary is fission based.
The secondary stage is based on fusion (tritium & deuterium, or compounds as LithiumDeuteride).
But this class can be further divided into two subclasses:
- The "clean" H bomb. This has a primary (fission based), and a second stage which is primarily fusion based.
- The "dirty" H bomb. In addition to above, a large casing of U238 surrounds the device. The secondary stage
produces enormous fluxes of fast neutrons, causing the mantle of U238 to fission too, greatly contributing
to the energy output of the weapon.
Very small nuclear weapons:
The large nuclear devices can be as large as several hundreds of kiloton (kT), or even several Megatons (MT),
of explosive power. However, very small downsized devices have been devised too. In quite a few articles
one can find an (rather) arbitrary boundary of 20 kT. Indeed, devices have been produced of just a few kT,
or even fractions of one kT. One example hereof, are artillery shells, which were in service up to 1991.
Obviously, these were tactical weapons (e.g. near a frontline).
Several techniques were applied. One technique is to bounce back scattered neutrons by a reflector around
the plutonium "pit". There is indeed a relation between the thickness of the reflector and the needed amount
of Plutonium (critical mass). Secondly, using well-timed wavefronts (also non-spherical) due to conventional
explosives, it turned out that one could compress subcomponents of the Plutonium pit even much more
compared to the traditional implosion technique. And lastly, using a hollow pit, or layer of Tritium/Deuterium,
boosting of fission can be achieved, due to the large flux of neutrons of the fusion reactions.
2.1.2. The 3rd generation.
In time, knowledge grew on how to utilize neutron absorbers and enhancers inside the device,and refinenments in stages.
From the early '60's, up to the '70's, '80's, the "ERB" weapons were in development. ERB is short for
"Enhanced Radiation, Reduced Blast". Sometimes they are also called "ERW", or Enhanced Radiation Weapons.
A popular variant is the "neutron bomb", where indeed the primary weapon function is radiation,
accompanied with a lower "blast" (but there will always be a rather significant blast).
In principle, it's a thermonuclear device, but the architecture is optimized to let neutrons escape
the weapon, instead to use neutron reflectors to bounce fast neutrons back, which would enhance
efficiency of the "blast".
The neutron bomb was often envisioned to be used in (rather) local areas, for example, to kill soldiers
but not to harm materials "too much". In such a scenario, the amount of fissile material was on the low
side anyway. Ofcourse, still any nuclear weapon today, uses fissile materials, although compounds
or gasses of light elements (releasing tritium, deuterium) would boost the weapon due to a high flux
of neutrons. A neutron bomb is thus optimized for high fluxes of neutrons.
You might find schema's suggesting a "fission free" neutron bomb, but those are not a reality yet.
Some people call such devices (like the ERW weapons), nuclear weapons of the "third" generation.
Also, in this same generation, some really strange (or rather insane) variants were proposed.
For example, the "Cobalt bomb", would use a thermonuclear device as it's core, and a very large quantity
of Cobalt surrounding it, producing (on detonation) a radioactive Cobalt isotope, that potentially
could cover (fall-out) on a whole continent, or even a large part of Earth (depending on the amount of Cobalt).
It's an absurt scenario, ofcourse, but I am sure that some "deep studies" were indeed performed.
2.2 The 4th generation.
These are not a reality yet. However, science is rather unstoppable. Also, when sufficient funds are provided,and/or facilities are provided, then this generation may come into existence.
Although a very clear definition of the 4th generation is still missing, it's obvious that it must
be different from all that we have seen above.
The fourth generation is arguably essentially about furher downsizing. There are multiple roads here.
Most folks think that "pure" fusion (without the fission stage) might form the basis for the 4th generation.
However, many other folks have serious doubts on the reality of future "pure fusion" weapons.
Increadably, since "pure fusion" is often seen as the coming archetype for 4th generation,
then the true payload then, might be very small, maybe even "pellet" size.
However, the "driver" that makes fusion possible, might still have quite considerable dimensions.
Ofcourse, the above statement at this point, is still fully hypothetical.
Various technical studies have been performed, rather recently, and are still ongoing.
Once chapter 3 is done, we have knowledge about the principles of fission and fusion,
and we can return, more prepared, to the specifics of a pure fusion weapon.
3. The basic principles of fission and fusion.
This is an optional chapter. If you do not like diving into some principles of Physics,you might move on to the next chapter.
3.1 Some principles first.
3.1.1. The Atom number.
The number of protons in the nucleus of an atom, is called the "atomic number". However, apart from Hydrogen (H), therewill always be a certain number of (neutral) neutrons as well. Since protons are charged positively, you might say that the
classical Electromagnetic force will immediately drive them apart. However, at short distances,
the strong nuclear (attractive) force between protons and neutrons, "rules".
Ofcourse, today physicists know of a (theoretical) deeper structure (quarks, gluons), but that does not play
a role in this simple note. As a part in the "standard model", quarks are seen as the constituents of
protons and neutrons. They play an important role in Quantum Chromodynamics (QCD).
So, a nucleus of a certain atom (or certain "element"), contains protons and neutrons. The number of neutrons may vary slightly,
resulting in socalled isotopes of that element.
For example, the element Cobald is often written as: 2759Co, meaning that the atom number is "27"
(which is the number of protons), while the total of protons and neutrons is "59" (the mass number).
So, in the upper example, the number of protons is 27, and the number of neutrons is (59-27).
As another example, one isotope of Uranium might we written as 92238U.
The "type" of atom (like Cobalt), is determined by the number of protons. Or stated in an equivalent way:
The atom number (number of protons) defines the sort of "element", like Hydrogen (H), Helium (He), Carbon (C), Iron (Fe) etc...
The total mass of the atom, is determined almost fully by the nucleus (all protons+neutrons).
So, in general, if we consider element "X", then it might be notated as ZNX, where
"Z" represents the "atom number" (the element actually) which is equivalent to the number of protons,
and "N" represents the "mass number", which is equivalent to the number of protons and neutrons together.
When considering a certain element, "N" might vary slightly, resulting in the various isotopes
of that particular element.
The nuclear force is extremely strong. However, it only operates in the range of femto meters,
which is very small indeed.
The classical Electric force (between the positively charged protons), is also large, and,
according to the classical ElectricDynamical theory, only diminishes by 1/r2.
So, protons at the "rim" of the nucleus would experience a large repulsive force. In a simple model,
the neutrons and protons are sort of "mixed" throughout the nucleus, so, thanks to the presence of
neutrons nearby those protons, the attractive nuclear force still holds the nucleus together.
Indeed, Jip and Janneke language, but that will be better formulated later on.
3.1.2 Electronshells in the Atom. Quantumnumbers and Atomic theory.
Atomic physics, enables to familiar ourselves to "quantum numbers" and orbitals,which define the state of an electron "around" the nucleus.
The theory is not too hard, and later on we will reckognize some of those features in nuclear theory,
since the "shell model" of the nucleus is important in nuclear physics too.
Let's take a look at the electrons "moving around" the nucleus in "certain orbits". Actually, such a picture
is wrong. However, everybody knows this classical picture of a number of electrons "moving around" the nucleus.
In figure 2 below, this is depicted by illustration "1".
Fig. 2: Some illustrations of electrons around the nucleus of an Atom.
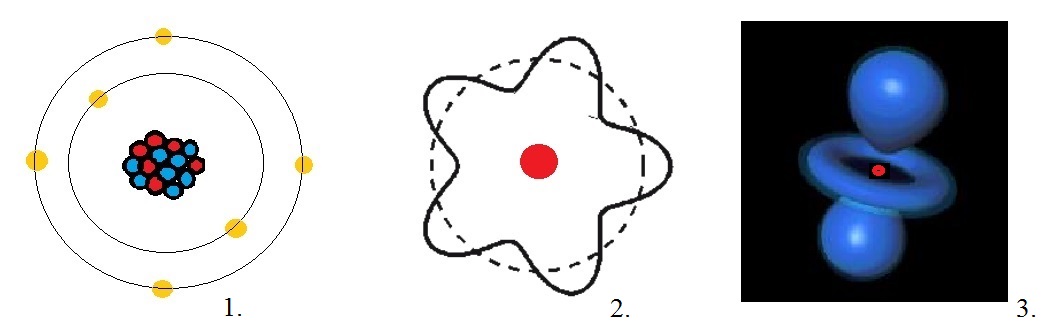
Source: My own Jip Janneke figure.
Even according to classical theory, such an electron would quickly spiral towards the nucleus
while emitting radiation.
Quantum Mechanics (QM) delivers us a reasonable model which explains the stability of the electron shells.
Near the end of the 1800's and the early 1900's, some amazing experiments were performed.
While the "classical" theories (electrodynamics, classical mechanics), made a clear distincion between particles
and "waves", some experiments pointed towards a more dualistic character of entities.
For example, particles that were beamed through a "double slit", created an interference pattern,
a phenomenon of which it was formerly thougth, that it could only be produced by "waves" like electromagnetic radiation.
As another example, the photoelectric effect showed that light, at certain circumstances, behaved like particles,
like transferring momentum to a real particle (such as an electron).
So, at certain observations, particles could behave like waves, and the other way around, what was traditionally seen
as waves, could behave like a particle.
Especially in the early days of QM, a theory called "wave mechanics" was often used to decribe quantum systems
like a particle. Intuitively, a wave like description of a particle, also means a certain distribution
of that particle in space, instead of talking purely of a "classical point particle".
Around 1924, 'De Broglie' showed, that there exists a "relation" between momentum (p) and wavelength ( λ),
in a "universal" way. In fact, it's a rather simple equation (if you see it), but with rather large consequences. It's this:
p = ℎ / λ
where h is Planck's constant. Now, "momentum", at that time, was considered to be a true 'particle-like' property,while 'wavelength' was understood to be a typical 'wave-like' property, which for example stuff like
light and radio waves have.
So, what description would fit an electron around a nucleus better? One thing which you might propose
is a "standing wave", as depicted in (2) in figure 2 above.
In such a case, we do not have a moving point particle, which would quickly moves towards the nucleus, anymore.
In such a case, you might say that the "orbital" must obey the condition 2πr = nλ
where λ is the wavelength of the electron, and n is a discrete number, and 2πr is the
circumference of the "orbit".
Ok, in this case you would have neatly placed "n" wavelengths along the orbit: hence a standing wave.
Note that in such description, you have imposed a sort of "quantization", by requiring that 2πr = nλ.
The QM description, however, is somewhat more elaborate.
Often, for the wavefunction of the particle, a notation like Ψ(r,t) is used.
It should attend you to the fact that (unmeasured/unobserved), it is distributed in space,
since we can vary "r" (the position), and that might produce regions of higher probabilities of finding the particle,
and regions of lower probabilities (just as you might expect from a wave-packet).
To search for the states of electron, you might consider the general atom, having Z protons, thereby
having a Ze positive total charge.
However, a study of the Hydrogen atom (1 proton, 1 electron), is good enough for discussing
quantum states and orbitals of the electron.
As Schrodinger found, the energy relation (equation) for Ψ(r,t) (or Ψ(r), leaving out "time"
for a moment) is:
| iℏ |
∂ -- ∂t |
Ψ(r,t) | = | - |
ℏ2 -- 2m | Δ Ψ(r,t) | + | V(r) Ψ(r,t) |
This equation is not so special since it essentially says Etotal = Ekinetic energy + Epotential energy
Not ready yet.
3.1.3. Radioactive decay (natural radioactivity).
This subsection is not really neccessary (as I realize myself now), but I leave it anyway.The advantage is that we get a quick intro in some nuclear "equations".
The "notations" used is in typical "Albert style", so, it really could be better and neater...
If you are new to this all, you better "google" on nuclear equations, and see how it is properly done.
There are several types of "spontaneous" radioactive processes, or you may also say "natural radioactivity".
(Not all are listed here (!))
Example: β decay.
It's possible that in a nucleus, a neutron "flips" into a proton, and thereby emitting a fast electron (e-),
and a "anti-neutrino" (-υ) as well.
It can actually happen with a "free" neutron too.
Ofcourse, "flips" is not an explanation. Particle physicists have a theory that fundamentally describes that process.
In this note, we do not have to go into depth, because it requires a discussion of the "weak" force, the W bosons, and quark types.
A reasonable explanation is this:
The strong force between nucleons (protons/neutrons) acts mostly and attrctively, between nearest neighbours.
At the same time the ElectroMagnetic coulomb repulsion, acts between all protons. So, that's a tendency
to drive them apart.
In such a sense, the presence of neutrons then acts as the glue which hold the particles in the nucleus together.
However, there is a limit to such usefullness of the number of neutrons.
Or in other words (semi-classical): The neutrons acts to screen the protons from each other, making the nucleus stable.
You might say that for effective screening there needs to be a little more neutrons than protons.
As said above, the socalled weak force is responsible for β decay.
However, the resulting proton (from the neutron) must be able to find a free quantum state (Pauli exclusion principle).
The higher the neutron/proton ratio, the more "chance", of having a free state for the "resulting" proton,
and the more chance on β decay.
In β decay, we have:
n -> p + e- + -υ
where "n" is the neutron, "p" is the proton, e- is the electron, and -υ- denotes the anti-neutrino.
If it happens in the nucleus of atom X (or atom of element X), we would have:
ZA X -> (Z+1)A Y + e- + -υ
Since a neutron was "changed" into a proton, we thus have an atom of element "Y".
Above is an example of β- decay (there also exists the β+ decay).
Thus in real example, we may have:
53131 I -> 54131 Xe + e- + -υ
Example: Alpha decay.
A relatively "unstable" nucleus, may even emit an α particle, which is essentially a He (Helium) nucleus (24He).
Or stated in other words: α particle decay is the phenomenon whereby an unstable nuclei goes into a stable state,
by emitting an α particle.
For example:
92238U -> 90234Th + 24He
Here, an Uranium isotope decays into Thorium, and an α particle is emitted.
Interestingly, a classical potential barrier would not allow that. However, Quantum Mechanical "tunneling"
through barriers, is possible. So, there exists a "means" to go from unstable to stable.
Alpha decay, is often followed by the emission of a high-energy γ photon, since the result nucleus, is often
still in an exited state.
3.2 A short description of Fission.
Quite some isotopes of elements, are "unstable". Sometimes, an nucleus can "break up" into two (sometimes 3, 4)roughly "equally heavy" elements, while also producing radiation, and/or particles of some kind, and energy.
This is often called "fission".
It is generally more often observed with isotopes with higher masses (the "A" number of ZA X).
Since those two parts are more stable than the original, it seems rather logical that energy gets released.
But there must be more than that.
In fact, a full (complete) explanation is not deviced yet, but very good "pointers" go around.
It's even not very obvious to cleary define "stable" and "unstable" elements.
For example, if about half of a certain amount of an isotope of an element, decays in 107 years,
then it is not so very stable, but also not so increadably unstable as well.
But for another isotope, it might be something like 5 years, then we may say that's quite unstable.
A detailed examination of decay requires isobaric spin, other quantum numbers, possibly shell theories, flavours etc..
That's not neccessary for us to do so.
Increadably, for my purpose, we can come away with a few pointers, and one is just the binding energy.
3.2.1. Binding Energy:
In semi-classical language:The mass of a nucleus is always less, than the sum of all of the individual masses of the protons and neutrons.
The mass difference corresponds to an energy E = Δmc2, which is ofcourse one of Einstein's
famous relations. This mass difference is also often called the mass defect.
When protons and neutrons comes close, and react together in making bonds, to form a nucleus, in that process energy is released,
which then (sort of) will "sit" in the "binding energy".
One can talk of the binding energy of an individual particle (proton/neutron), or consider the total binding energy.
As an example of such individual value, you might think of a number like 8 MeV.
In some articles, "binding energy" is characterize as negative energy, which *might* be a bit of an unfortunate term.
It's probably better to say, that if the "binding energy" increases, the particles are "deeper in the well",
thereby making their bonds stronger.
So, if an nucleus has a high binding energy, in general, it's more stable.
In the latter part of first halve of the former century (say 1935), nuclear physicist already did enormously much
experimental work, and many hypothesis were proposed. Gradually, great theories were deviced.
It's pretty useless to give here a fairly accurate equation of calculating the Binding Energy.
However, I think it's a great illustration. It's a formula from around that time (Weizsacker's formula).
It's from around 1935:
EB = av A - as A2/3 - ac Z2 / A1/3 - aA (A-Z)2/ A + δ(A,Z)
There are several terms, like an Area component, a Coulomb component etc..
The formula is partly theoretical (thus created by theory) and empirical (values from measurements).
Except for the very light elements, it works.
The figure below, shows the binding energy (per nucleon, that is, proton or neutron) along all elements.
Note that the figure rises very sharply, then has a maximum for in the "neighboorhoud" of Iron (Fe), and when
the massnumber increases, the slope is pointed downwards.
Ofcourse, pure Hydrogen (11H), only has one proton, so, the binding energy does not really apply here.
Then, for the next light elements, the slope is very steep.
Fig. 3: Average binding energy per nucleon, against the mass number (the elements)
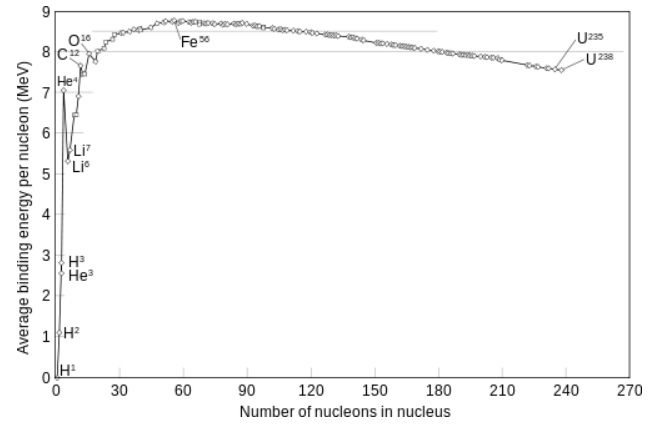
Source: Wikimedia commons.
It also means this: Suppose some heavy Uranium isotope, breaks up into two smaller parts (e.g. 140Ba and 93Kr),
then from figure 3, you can find the difference in binding energies, from Uranium, and the two fragments.
Remember that the figure above, illustrates the binding energy per nucleon.
Taking all nucleons together, we may have an energy release of something in the order of 200MeV.
3.2.2. Fission of some specific heavy isotopes, and chain reactions
Some heavy isotopes may undergo fission, only after capuring a fast neutron like 238U, while otherisotopes may undergo fission after capuring a slow, or "thermal" neutron, like 235U.
This behaviour is found to be related to the number of neutrons in that nucleus, and whether the total is an even
or odd number.
In general, low-energy (thermal) neutrons are able to cause fission only in those isotopes of Uranium and Plutonium
where the nuclei contain odd numbers of neutrons (that is: 233U, 235U, and 239Pu).
Thermal neutrons
Some heavy isotopes are rather "succeptible" to thermal neutrons.A thermal neutron is considered to be a relatively "slow" moving particle. If a rather potential unstable nucleus
like 235U, caputures that neutron, we have a very short phase of 236U.
There are several models, like the "shell" model, or the "liquid droplet" model, which might give us
a high level understanding of the nucleus and structure.
Using the "liquid droplet" (Gamov, 1930), it's rather easy to understand the fission of such large isotope.
That 236U nucleus is immediately in an excited state, and starts to oscillate, and the moment a small "neck"
begins to form, the short-range "(nuclear) strong force" will lose from the electric Coulomb force,
which will tear the two parts apart. Hence, we have fission.
What's rather disturbing, is that this sole nucleus, undergoing fission, will produce not only the the two new nuclei,
(e.g. 140Ba and 93Kr), but also 3 neutrons.
However, the neutrons produced at the fission path in figure 3, are, with a high probability, highly-energetic,
or fast neutrons.
Suppose you have a densily packed piece of optimized heavy isotope(s), then fission of one nucleus,
will possibly "ignite" other 235U nuclei, which may undergo fission, which will produce neutrons,
which will ignite still other nuclei etc.. etc.. Such process will go extremely rapidly.
In effect, you may have a chain reaction.
In the early days of A-bombs (pure fission weapons), scientists tried to find an architecture, which would
create the best environment to produce such a fast chain reaction. In the early days, it was often an puzzle
whether fast-, or thermal neutrons, and the use of moderators, would provide the best results.
Fig. 4: Simple illustration of one possible fission path of 235U
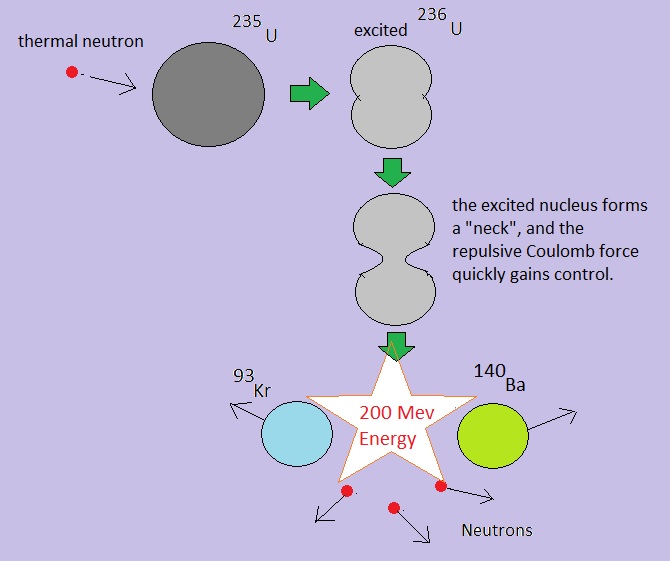
Source: my own "Jip en Janneke" figure.
By the way, there are multiple decay paths from 235U. That is, other fragments than 140Ba and 93Kr, may form.
The nuclear equation for the fission depicted in figure 4, is:
01n + 92235U -> 56141Ba + 3296Kr + 301n + 200 MeV
Fast neutrons
When fission occurs only after capuring a slow thermal neutron (<10keV), or fast neutrons (>1MeV),the isotope is called a "fissile" isotope, like 235U.
But when only fast neutrons (>1MeV) will produce fission, the isotope is called "fissionable",
like 238U.
A better way to characterize fissile isotopes, is to say that their decay process (fission) may "ignite" other
nuclei to do the same, since the fast neutrons may be captured by those other nuclei.
So, they may split up too, while they again emit fast neutrons (most often 3 neutrons)
This is also often called "chain-reaction".
When the mass and concentration is high enough, extremely fast successions of chains may occur.
The decay chains of 238U is rather complex, involving many steps. Many "by-products" can
form, and 238U may for example start to emit an Helium nuclues and form Th:
92238U -> 90234Th + 24He
Here, an Uranium isotope decays into Thorium, and an α particle is emitted.
It may also capture a thermal neutron and transmutates into 239Pu. This latter one is
beneficial in a Nuclear Reactor for energy production.
238U is the most abundant isotope of uranium found in nature, something around 99%.
It has a very high half-life, which explains why we still find it in Nature.
It almost cannot perform chain reactions, since it has a large chance to scatter neutrons,
and in particular give rise for inelastic collisions. However, high-energetic decays can occur.
Although the "fissile" isotopes 235U and 239Pu are important in pure fission weapons,
or the first stage of a thermonuclear weapon, even 238U may play a role in nuclear weapons.
While 238U does not exhibit chain reactions, it may fission under a very high neutron flux.
So, in boosted- or real thermonuclear weapons, even depleted 238U may be may be used
to contribute in the total energy output. This fact may surprise you, since 238U is rather common.
3.2.3. More on fissionable, and fissile, elements.
- A "fissile" element (isotope of an element) can undergo fission with a higher probability,if it captures a (slow) thermal neutron. But they can undergo fission too with capturing a fast neutron.
This sort of isotopes might cascade in fast chainreactions, depending on e.g. density, amount, geometry..
-The term "fissionable" is slightly different from above. A fissionable isotope can undergo fission
when it captures a high energy neutron (> 1MeV).
But this sort of isotopes will not cascade in fast chainreactions.
Thus: All fissile nuclides are fissionable, but only some fissionable nuclides are also fissile.
Important is to remember:
-238U will only undergo fission using fast neutrons, thereby it is "fissionable",
but not "fissile".
-235U and 239Pu will undergo fission having slow, and fast neutrons,
although the "cross-section" for slow neutrons is much higher.
And what's important here, is that the non-fissile isotopes often display scattering,
thereby preventing (in itself) a chain reaction. But they can fission.
A more consistent way to distinguish between fissile and fisionable isotopes, is the fact
that "fissile nuclei" may participate in chain reactions, while fissionable isotopes
generally don't do that, for example, because the neutron scattering is too high.
A special thing in Nuclear reactors is, that 238U can transmutate into 239Pu,
which is quite common in Reactors.
A relevant portion of the energy then comes from the fission of 239Pu.
In most reactions, two lighter elements are the result of the fission, while typically also neutrons are produced.
Those two lighter elements are in the range of mass number 90 (plus/minus a few) and 140 (plus/minus a few).
If after capturing the slow neutron, the probability of fission is "high", then indeed the term "fissile" is used,
and a chain rection may result if the nuclei of that isotope are close.
Especially fissile isotopes are 233U, 235U, 239Pu, 240Pu and 241Pu.
The isotopes 235U and 239Pu, are the main "succeptible" isotopes in fission chains.
You might expect those as main candidates for nuclear weapons. True, but many multi-stage weapons use fusion in some
middle stage, produce many fast neutrons, where a substance like the fissionable 238 comes into play.
Nuclear Reactors:
Nuclear technology is wide and deep. This is also true for Nuclear Reactors in civil live.
Some types of Reactor plants, may even be used to "breed" fissile material.
Thus it indeed may be troublesome, if an unstable nation (but who am I to judge that), has
a nuclear plant, or wants one.
For any nation in possesion of Nuclear plants, it must hold that strict inspections are absolutely mandatory.
With respect to nuclear energy in civil live, many folks are "pro" and many are "contra".
If you would like to know my opinion: I myself do not like, or want, nuclear energy at all, with an exception:
Having facilities for producing certain isotopes for medicine, is absolutely critical.
Even for just this fact: you cannot or may not "ban" nuclear facilities completely, since production for
medical purposes is extremely important.
3.2.4. Critical mass.
If one have "fissile" material (see above), and a efficient means for starting neutron showers,a self-sustained chain reaction could really possible, if certain conditions are met.
The term "critical mass" is often heard in this context.
It's not an absolute figure, since densely packing, appliances for neutron showers, temperature,
geometry, the purity of fissile material etc.. has a strong influence on what the "critical mass" is,
in a certain situation or device.
For example, you might have a certain amount of fissile material, but for several reasons,
the chain reactions are not self-sustained.
Maybe your material is not pure enough, not dense enough, too little material, no neutron reflectors etc..
It might be better to read "critical mass" as "density/geometry/amount/neutron-initiater".
The very first pure fission bombs, used a spherical design, where at an outer sphere
at many wellchosen places, fissile material was located. Behind it, convential high explosives
was stores which would shoot with an extreme speed those fissile fragments as "a front" to the centre, where also
and amount of fissile material was present. Precisely at the core, it's likely that some neutron initiator
(for creating a high flux of neutrons) was present too.
This setup, created a situation that, just before detonation, the "critical mass" was met, and a
detonation followed.
The setup described above, is often characterized as the "implosion method".
So, it's important to understand, that critical mass, is not simply the "amount" of fissile material.
By the way, in the first pure fission devices, it is known that the "efficiency" of actual fission,
was rather low. Meaning that a certain amount (a certain percentage) of fissile material remained intact.
3.3 A short description of Fusion.
3.3.1. General principles.
Figure 1 remains illustrative, also for this section too.If you "go" to the left, from the most heavy isotopes, to "medium weight", then you can see a significant
difference in "binding energy" per nucleon.
Likewise, if you go from the lightest isotopes, and stop somewhat before Iron (Fe), then you again can see
a significant difference in "binding energy" too.
Although quite a few lighter elements might be thought to be candidates for fusion, it has turned out that Nature
favours the Hydrogen (H) isotopes, Deuterium (12H) and Tritium (13H).
A simple explanation is that the H isotopes only have one proton, thereby making the repulsive Coulomb force
weaker compared to the elements with more protons.
Once the individual nuclei are very close, the strong attractive "nuclear force" starts to become in effect.
Here too, the masses of the individual constituents are larger, than that of the resulting element.
In other words, the mass of the combination will be less than the sum of the masses of the individual nuclei.
Again, this mass defect is equivalent to "energy", and Einstein's famous equation works here too: E = Δmc2.
Below, the famous, and often used "Deuterium Tritium" fusion reaction, is shown:
12H + 13H -> 24He + 01n + 17.59 MeV
You can see that the result is a Helium nucleus, plus a neutron, and 17.59 MeV.
Quite a few other fusion events (and corresponding equations) are possible.
Here is the "Deuterium Deuterium" fusion reaction:
12H + 12H -> 13H + 11H + 4.03 MeV
To start fusion, the individual particles needs to get very close, in order that the "nuclear force" starts
to get working. The "range" of this force, is very small.
It simply means that the velocity, or Energy, of the individual particles must be high, or, in other words,
the Temperature must be very high. In Thermonuclear devices, the first stage of the weapon is "fission" which produces
an enormous pressure, radiation, and Temperature, which is the trigger to get fusion working.
Note:
The processes might be a tiny bit more complex. Sometimes the weak force may "turn" a proton into a neutron,
or the other way around. Althoug such an event may not generally happen "often", it can result in another
sequence of "end products".
Note:
It can be fun to do a websearch of the fusion chain inside the core of the Sun.
If you like that, you can even compare young stars, and heavy stars which enter
the final stages of their life.
For example, for a Red Giant, at a certain stage, the Temperature can get high enough for more
heavier elements to start to "fuse".
3.3.2. Crossections, Detection, scattering, and production neutrons.
Crossections, and Detection:A neutron has no electrical charge, and this fact makes it somewhat more difficult to detect.
Other forms of radiations, like the well-known α (Helium nucleus)-, β (electrons)-,
and γ (high energy photons) radiation, have well known interactions with other matter.
For neutrons, it makes certainly sense to talk about "cross section". It also makes sense to talk
about the wavelength of a neutron (shorter or longer, depending on it's speed or energy).
One way to detect neutrons, is that some nucleus "captures" it, and consequently this nucleus
may decay into another element, thereby also emitting α, β, or γ radiation, which is more easy to detect.
Some elements have a "large" cross section for capturing thermal (slow) neutrons, like 10B (Boron).
Fast neutrons are then first often slowed down (by some material), and next are detected by some method like above.
Many sorts of detectors go around.
As it turns out, different elements have different crossections for reacting on neutrons with different "speeds",
which makes it even possible to generate "spectra" of neutron energies.
It's good to remember that "cross section" is a sort of relative measure, of how well a certain nucleus
is able to "capture" a neutron.
Scattering of neutrons:
According to Quantum Mechanics, to elementary particles, a wave-length may be asscociated,
which is related to it's energy (or impuls). The famous de Broglie relation describes that.
In this sense, when neutrons of a certain energy approach some material, then at some point,
this material looks a lot like a "grid" (or lattice) on which we can almost use classical wave theory
to calculate the amount (spectra) of "scattering" of those neutrons.
In some specific setups, the neutrons may penetrate very deep, but in other specific setups
(meaning the speed of neutrons, and the material used), many of such a neutron flux, may scatter (bounce)
to some very specific directions.
This feature can also be used in some thermonuclear devices. It "helps" to intensify neutron "showers".
Neutron shower:
Often, in nuclear weapons, some "neutron initiator/neutron multiplier" was used to produce the very first "neutron shower".
This can also be in the form of a "neutron source", producing a constant rate of neutrons.
Both methods can be in such a setup, that just before the intended detonation, a conventional explosion
presses U or Pu fragments with a high speed towards a pit, inside where also this intended neutron generator
is present. The high pressure then activates this neutron initiator.
As another solution, it's also possible that a small potential fusion mechanism (Deuterium-Tritium)
is at the centre, which can generate (fast) neutrons.
It can also be true that an external "neutron initiator" is present, in the form of a small accelerator,
which accelerates Deuterium- and/or Tritium ions, and let them slam on a similar target. This creates the fusion
process needed to generate neutrons.
Today these devices are even smaller than hand-held devices.
4. The basic principles of the Pure Fission- and Thermonuclear devices.
A nuclear device, "runs" on fast neutrons.Although the "crosssection" of 235U, or 239Pu, is very high with slow neutrons,
they can react on fast neutrons as well (they are fissile).
It's very instructive to see a chart with the value of the cross-sections, against neutron energy.
Thermal or slow neutrons will not efficiently generate the "fission cascades" in een large volume,
in an short enough period of time. But fast neutrons can.
Indeed, it's mainly fast neutrons, which maintain the fast fission chains in a fission weapon.
Already the initial analysis of Bohr and Wheeler in the early '40's, show why U235 will exhibit
fast-fission (no substages), in chains, as is required in a fission weapon, in a required
minimum of time, which is essential for superfast energy release and detonation.
The main types of implementations of nuclear devices, are:
-1. A pure fission weapon. It obviously uses "fission" only. The "fuel" might be 239Pu
or 235U, or a combination of both (and sometimes even also small amounts of other fissile isotopes).
-2. A "boosted" fission weapon. A pure fission weapon can be boosted by layers of Tritium and Deuterium,
or a central region with those H isotopes (or compounds which will quickly transform in Tritium and Deuterium).
This class is often not considered to fall into the real "thermonuclear" multi-stage weapons.
-3. Thermonuclear weapons are multi-stage weapons (often two stage), with a primary fission stage,
and a secondary stage which most often combines fission and fusion.
section 4.1 shortly discusses the "pure fission" and "boosted fission" devices.
Section 4.2 provide some crude examples of the true "Thermo nuclear" class.
Section 4.4 is concerned about the very first pure fission weapons, but with a strong accent on
the history of development too.
A nuclear bomb will not explode in the traditional way. No, the outer casing of the bomb "dis-integrates",
since in an extremely short time, radiation, and other manifestations of energy, is released.
One important feature of any nuclear device is "timing". In case of pure fission, a sufficiently amount of
cascade fissions (chains) need to have taken place, before the structure gives away.
Otherwise, the chance of a socalled "fizzle" is a reality, which we may describe as a yield of
very low intensity compared to what could have been reached.
Since fission is also a part of the boosted weapon, or even the Thermonuclear class, the same
principle holds here too.
4.1 The pure fission weapon and the boosted fission weapon.
Fig. 5: "Jip and Janneke" illustration of a pure fission- and boosted fission weapons.
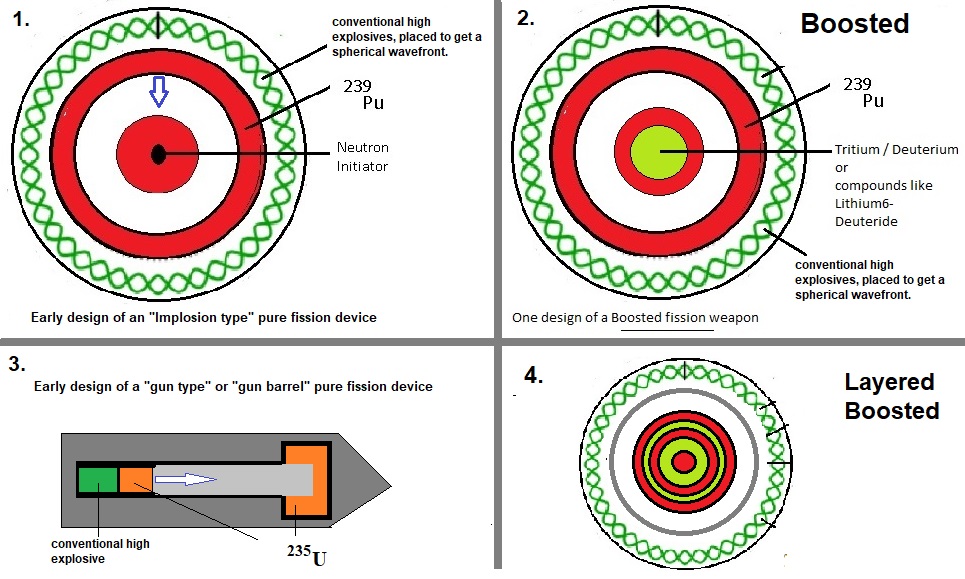
Source: my own Jip and Janneke figure. Very crude figures indeed. Some layers are "over" dimensioned for clarity.
-Pure fission:
The first image in figure 5 shows a pure fission device, using the "implosion" technique.In '45 (and later), other geometries were also used (like the gun-barrel, or gun-type geometry).
Most often, the setup displayed above, is implemented by most Nations.
Indeed, the figure suggests that this setup uses the implosion principle. The curled outer "shell" is supposed
to represent conventional high explosives, carefully arranged, in order that the Pu or U shell (the reddish ring),
quickly and uniformly compresses and hit the inner pit, with the maximum speed possible, in such setup.
Indeed, in less than microseconds (μ seconds) a supercritical environment exists, which almost immediately therafter,
will pass through a large number of generations of fissions.
In the compressed object, the mean free path of a fast neutron is short, and the probability that it gets
absorbed by another Pu or U nucleus is relatively high.
In the setup, it's rather difficult to obtain a high efficiency of 'total' fission.
In the literature, the figures varies somewhat, but often only 20% of full fission is reached, before
the bomb structure totally gives away (disintegrates).
Critical mass (needed to start fast chains of generations of fission), is a relative number.
It depends on the amount, density, geometry, and other factors, but certainly also on how efficient neutrons
can interact with the nuclei.
Triggers/Timers for the outer shell(s):
(1): Old fashioned Krytrons:
The outer shell of conventional explosives, must detonate in a precise and orchestrated manner.
Often, these explosives are arranged in "lenses", which must detonate simultaneously. This way, the pressure
exerted on the core from all sides is uniform. The shock wave from these explosions compresses
the fissile material inside the core, and starts the fission process.
This is a very critical process, in order to avoid a fizzle.
The seperated lenses consisting of conventional explosives, are ignited by Krytrons, which are fast switches
producing an output Voltage/Amperage to ignite the explosive material in such lens.
It works smarter and faster than ordinary "caps".
Depending on the Geometry of the devices, different sorts of conventional explosives might be used,
all working together, in order to reach a uniform compression of the core.
Thus, different sorts of timing issues must be resolved, and "plugs" like Krytons partly solved that.
(2): Exploding-bridgewire detonator EWB:
Actually similar in usage as in (1) described above. The point here too, is a sharply timed output V/A,
which garantees the detonation of a lens at a precise point in time.
-Boosted fission:
Usually, relatively small amounts of Tritium and Deuterium can be used to "boost" the fission net result.It's not really targeted to increase the energy output directly, but to increase the total efficiency of fission.
A major goal is downsizing of the nuclear device, and reduce the need for larger quantities of Pu or U,
and reduces the need for very strong structural supports.
The setup displayed in image 2, is rather similar to image 1, except for the addition of Tritium/Deuterium,
most often located in the central core of the device.
The process starts as already described in the subsection above, However, at the time only a relatively smaller
part of fission occured, the conditions are met for a limited fusion process. This sets off an intense neutronflux
radially outward, increasing the chance of fission of individual nuclei, in cooperation with the chains which
would already occur anyway.
The net-result is a very efficient fission process, greatly improving the energy output, compared to
the original setup displayed in image 1.
4.2 The Thermonuclear class (H bomb).
Please take a short look at figure 6 below.Modern bombs often start with a pure fission "trigger" (the primary stage), which in itself is a large powerfull
device, ofcourse.
It might be an implosion type of device, where conventional explosives, generate a carefully designed wavefront
which pushes sub-critical pieces of Pu (or U) towards a centre. Immediately a supercritical object exists, and
if an neutron initiator creates a neutron flux, a cascaded fission starts (chainreaction), timed in μ seconds.
After a number of generations of chains, the energy release in X- and γ rays, is already so enormous,
that the temperature must be expressed in millions of degrees Celcius (or Kelvin), enough for fusion to start.
The device still did not exploded, since a little more time is needed.
Meanwhile, still in μ seconds, the foam turns into plasma, and neutrons bombards the secondary stage.
The secondary stage reacts in the most violent way and fission and fusion takes place.
A more scientific explanation will go into the details that the second stage ignites due to a
"radiation initiated" implosion of the second stage.
Next, the bomb fully disintegrates. Next, a short intense light flash is visible, as observed from large distances,
mainly due to interaction of X- and γ rays in the environment. Immediately followed by an energy "ball", which as you
have seen with the Trinity test (figure at the start of this note), easily expands to hundreds of meters in size,
in just a few miliseconds.
If an outer layer (or tamper) of 238U exists, than we can think of it as if a "third stage"
is present. The enourmous neutronflux of fast neutrons, will fission a very relevant percentage of that
238U material, which significantly adds to the total energy release of the device.
Note:
Most often however, a third stage is percieved as another secondary stage, physically present in the device.
This way, you can repeat (to a certain limit) the secondary stages in the bomb.
In the following two sub sections, two examples of Thermonuclear weapons, will be touched upon.
Some more architectures exists (or have existed), but I believe that two examples will suffice to provide
a general idea of the architecture of such weapons.
Where below 239Pu is shown in the figures and text, might in some other implementations
be replaced by 235U.
4.2.1 Spherical setup of a multi-stage Thermonuclear weapon.
Fig. 6: Simple illustration of a multi-stage Thermonuclear weapon.
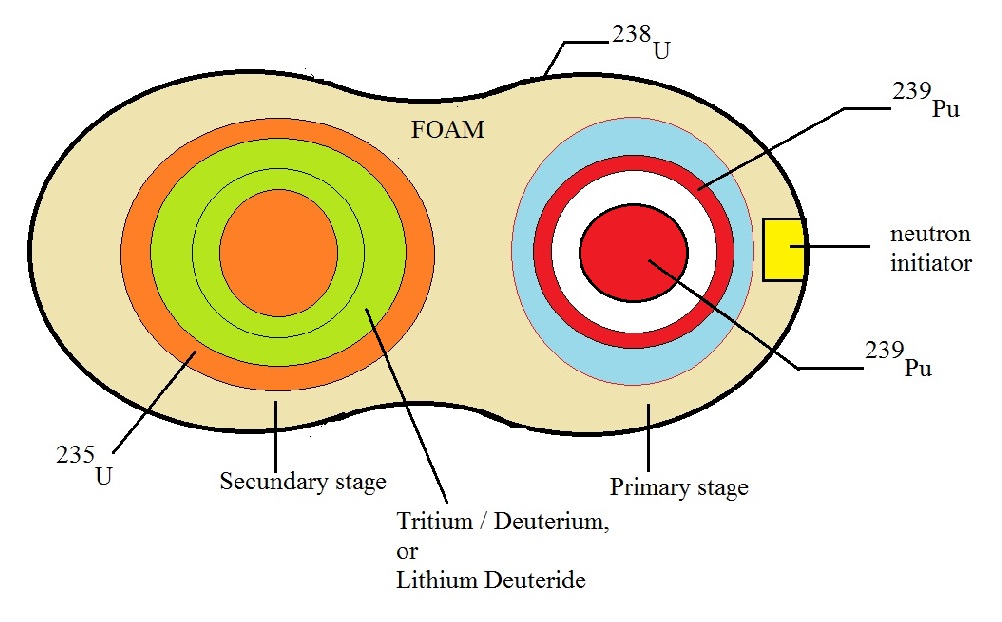
Source: my own Jip and Janneke figure.
Ofcourse, true usable (workable) details, really only exists in classified literature.
Well, at least that's what I hope is true.
Suppose, just hypothetically: If someone would found true clear workable details in some accessible document,
like e.g., on the internet, then that would be Treason at the maximum level, by the perpetrator.
Figure 6 is not detailed at all.
Primairy Stage:
It is true, that the primary stage often is a pure fission component.
However, it could also contain a fusion substage (container with Lithium(6) Deuteride, or Tritium/Deuterium).
In this case, the primary is often called a "boosted" primary.
Figure 6 suggests that the primary stage uses the implosion principle. The blue outer "shell" is supposed
to represent conventional high explosives, carefully arranged, in order that the Pu or U shell (the reddish ring),
quickly and uniformly compresses and hit the inner pit, with the maximum speed possible, in such setup.
Indeed, in less than microseconds (μ seconds) a supercritical environment exists, which almost immediately therafter,
will pass through a large number of generations of fissions.
From former sections, you might remember the "critical mass". It's not just an amount of mass.
Using neutron reflectors, like shells of Berrilium, you can increase the efficiency of fission, that is,
more generations of chains in a shorter amount of time. Indeed, part of the neutronflux that would otherwise
have escaped, now bounce back.
The compounds used, and the geometry of the primary stage (like having neutron reflectors), greatly influence
the needed mass to have an extremely fast and intense fission rate, and thus how fast energy (heat),
and radiation is produced.
Without those elements, the downsizing of modern weapons, and the yield, would not have been possible.
Note that with this elementary description of the Primary stage, there is no further need to describe
the pure fission weapon any further.
Secondary Stage:
In figure 6, both the Primary- and Secondary stages, are spherical. However, for many real-world designs,
the secondary is cilindrical. For our purpose, it's not so important, since in this note we only want
to describe the primary processes.
For the overall "shape" and geometry of the setup, the casing where the primary- and secondary are mounted in,
is supposed to reflect much of the X- and γ radiation, towards the secondary.
This is represented in figure 6, by the "peanut-shape" of the inner casing.
High pressure, -energy, -temperature, and bombardment by fast neutrons from the primary, will ultimately
setof the secondary. There are many practical considerations, on how exactly, the secondary will go of.
One consideration, is on how to maximize the heat-transfer "rate" to the fusion fuel.
Another consideration is, how to make sure the Secondary undergoes a fast implosion as well.
In figure 6, The secondary is enclosed by 235U, with a similar "pit".
Just having a 238U tamper, is possible too.
This "pit" functions as a "spark plug". But this one may be absent too.
A global mechanism to offset the secondary, is that primary detonation first generates so much X radiation
so that the secondary compresses at very high velocity. If a fission spark plug is present, then this one
should give the last "push" to ignite the fusion. If a spark plug is absent, then superfast series of
shockwaves should converge at the centre of the Tritium/Deuterium compound, driving the Temperature
to the needed condition for fusion to start.
Once the fusion starts, again enourmous heat, radiation, and fast neutrons are generated.
Any 238U tamper, that is, a surrounding of a single stage, or even the entire weapon,
will undergo fission as well, strongly adding to the total energy release of the device.
There are ofcourse many details, which are not explained in this "Jip and Janneke" text.
- For example, if you look at the Primary, what would be the advantage of using such hollow shell design?
It seems obvious, that it's more easy to compress such a setup with an enormous velocity.
- As another example: the use and geometry of 238U tampers, is very complex.
Only the people who were involved in the extensive testing periods, that is, mainly the '50's
and '60's of the former century (USA, USSR), have gained an enormous knowledge on how to develop
effective thermonuclear weapons.
For having extremely large detonations (many Megatons), one would need a relatively large Primary stage too.
However, very large fission primaries are elaborous, quite heavy, and even dangerous due to the large amount
of sub-critical "parts" of fissile material. Often, it is limited to a max. of hunderds of kilotons
of explosive power.
For large detonations, a large Secondary is needed, and possibly even a Tertiary Stage.
4.2.2 Cilindrical setup of a multi-stage Thermonuclear weapon.
The example shown here, is also called the (older) "Teller-Ulam Configuration".Fig. 7: Simple illustration of the older "Teller-Ulam" weapon.
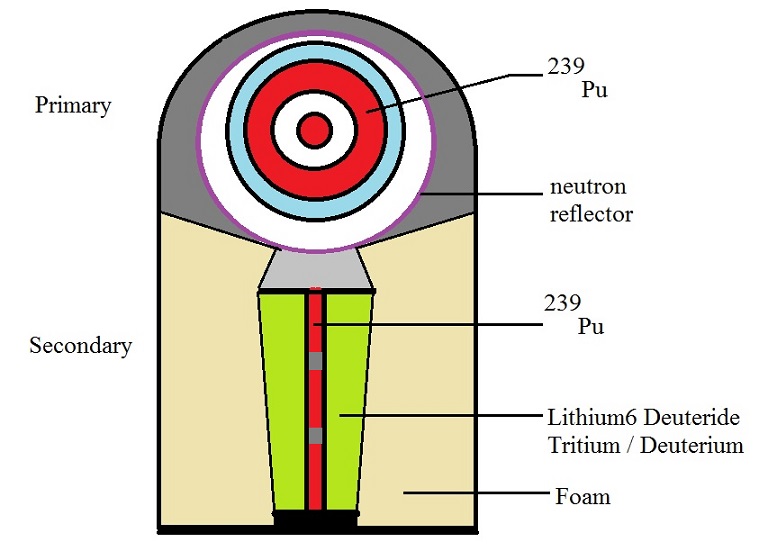
Source: my own Jip and Janneke figure.
Again, we might have a pure fission primary stage.
The main principle of such primary already has been discussed above.
The second stage too, is supposed to implode violently.
Heat, also contributed by foam, and most certainly of the energy due to the X rays, and
enormous pressure from the primary, will implode the secondary stage, where the Pu sub-critical parts
are compressed into a supercritical object.
This gives rise to an immediate fission chain, which generates the temperature needed
to support fusion.
Here too, the timeline must be measured in μ seconds.
It's possible that an 238U tamper (outer shell) surrounds the main device.
This enhances structural support at the very first stages of fission/fusion, and later
contributes to the total energy output since a relevant fraction will fission too.
Here is a YouTube vid, portraying the first true Hydrogen bomb (the US device "Ivy Mike").
The vid is probably a bit "coloured" by the mindset of the folks back then. However, the clip illustrates
"Ivy Mike" close enough. Note the large construction needed for a true large H-class bomb.
Ivy Mike, the Teller Bomb.
4.3 Other considerations
4.3.1 Fizzle
If you consider a pure fission weapon, or even a thermonuclear wapon, then having a bad design,might end up in a fizzle.
Let's take a look at a pure fission weapon.
Then a fizzle is essentially a device where a very low amount of fissile material actually fissioned.
In nuclear weapons, timing is very important, as well as how you have arrange the conventional
high-explosives, in order to compress the sub-critical parts. If that arrangement is not good enough,
then compression to a supercritical object may only partially take place, to a result that the enormous
pressure will detonate the bomb, before any significant amount of fission took place.
One keypoint is namely, (if using an implosion type of trigger), that the demands on the placement
of the conventional explosives is very high, and it must be very precise, in order to make sure
that a very uniform wavefront compresses the 235U or 239Pu materials.
So, you may view a fizzle as a failed detonation, where at most only a very small part of the fissile material
actually fissioned, resulting in a very limited detonation, and indeed, a very dirty one.
Note:
Implementing a fission weapon often uses the "implosion type" of design.
However, the "gun-type" of design, where a sub-critical part of fissile material
was shot (like bullet) to another sub-critical part, was used as well.
4.3.2 The "Dirty" Bomb.
Discussing regular nuclear weapons, the terms "dirty" and "clean" are also used (or mis-used).For example, having the smallest possible primary stage (using fission, which will always produce
radioactive byproducts), but a larger fusion component, might ultimately produce a lot of energy/heat
and neutrons, but a relatively lower amount of radioactive fall-out.
However, in public discusions, a dirty bomb has a different meaning.
It often refers to a conventional charge, with some potporrie of medium- to high radio active materials.
It ofcourse has nothing to do with a nuclear detonation: this conventional explosion then will simply throw that
radioactive stuff over a larger area, hurting many people.
It's extremely unlikely that terrorists are able to produce a real nuclear weapon.
But a "Dirty Bomb" seems not so hard to create.
I am sure that lots of Governmental agencies are studying this topic.
At least, I really hope so.
In the very unlikely event that they were not, then they should immediately do so.
4.4 Short description of the very first pure fission weapons.
Let's turn our attention on the history of the development of the very first few fission weapons.This section is absolutely ultra-thin, and only mentions some highlights.
It only covers, roughly, the period 1940 - 1950.
4.4.1 USA.
Then this must be about "Little Boy" and "Fat Man", and ofcourse "Trinity" (the very first nuclear explosion,executed as a test). Fat Man was very similar (but slightly improved) to the device used in the Trinity test.
- Both Trinity, and Fat Man, used the "implosion" principle, similar as to the "primary stage" of
a multi-stage weapon as we have seen above.
- In contrast, Little Boy used the socalled "gun barrel" or "gun type" technique.
The gun-barrel type, used as subcritical rod, which was (conventionally) fired into another subcrital rod,
which was slightly wider and hollow. The idea is thus that when the parts "merged", a supercritical object exist,
which, with help of a neutron-generator (if still needed), went through extremely fast generations of fissions.
However, there were serious issues when using Pu, originally thought to be the fuel for "Slim Man",
the predecessor of Little Boy. Indeed, the impurities of 240U in 239U,
fed the fear of "pre-detionation" into a fizzle (see section 3.1.2).
It's indeed so that "spontaneous fission" of 240U, might enhance the chance of a fizzle.
Ultimately, with Little Boy (the follow-up of Slim Man), 235U was used.
Contrary, the implosion principle could use Pu, since a highly delicated implosion "lens" of
carefully placed conventional explosives in an outer shell, would make it possible that subcritical parts
would be highly symmetrical compressed, and thus would make the needed time to form such a dense supercritical
object much smaller compared to the gun-barrel design. The chance on a fizzle is smaller.
Little Boy and Fat Man, were actually used on two Japanese cities, respectively on Hiroshima and Nagasaki,
in august 1945.
Fat Man might be viewed (as the predecessor to) the Mark III weapon, which was in service until 1949, and
that one was followed up by an improved (but largely similar) version in 1949, the Mark IV.
The Mark IV was absolutely more fault-proof, and used much longer lasting electronics, and also used
a removable composite pit (centre core), using Pu and U.
Then in august 1949, the Sovjet Union peformed it's first nuclear test, RDS-1, in Kazakhstan.
It was a pure fission bomb, most certainly based on the Fat Man, or the Mark III, design.
From then on, developments and testing (on both sides: USA, USSR) went faster and faster.
Let's take a super-quick look on the history of development of the very first weapons.
In the late '30's of the former century, is was discovered that fission of heavy isotopes
could produces large amounts of energy.
As you may remember of sections 2.1.1., 2.2.1 and 2.2.2, the energy release is much higher
per atom compared to pure chemical processes. By some physicists, it was realized that this
might be utilized in some weapon of some sort.
Then ofcourse, in '39/'40, WWII broke out. Still, many brilliant physicists were in Germany.
Fear existed among some insiders in the Allied forces, that Nazi Germany was underway developing
a nuclear weapon.
In a response, in the US, the socalled "Manhattan Project" started in '42, which ultimately resulted
in the Trinity test, and the bombs Little Boy and Fat Man in 1945.
Those three devices were by no means "rugged" and "time-proof". It is known that with Fat Man, some parts
of the electronics only lasted for a couple of days, and there were problems with the core pit too,
just to name a few issues. It simply meant that once fully assembled, then either use it, or
disassemble some critical parts.
The follow-up, the Mark IV (1949) finally was rugged, and preservation was relatively OK.
4.4.2 Sovjet Union.
Interestingly, the Sovjets did not lagged behind that much, in pure "theory", that is.Here too, in the late '30's, ideas were discussed among physicists to employ nuclear fission into usable weapons.
Only when through intelligence, the Russians learned about the Manhatten Project, and after several
notifications by Sovjet physicists to Stalin, finally the Russians slowly started their own project.
Historians do not doubt that several ocurrences of serious Russian intelligence took place
during the period '42 - '45, and even direct handsout of intel by some subjects (e.g. Fuchs)
that occurred, likely lowered the learning path of the Russians at that time.
But it was only after it became clear that nuclear weapons really were employed by the US in '45,
the Sovjets were fully triggered to go ahead at full speed, and build them themselves.
As already said above, in august 1949, the Sovjet Union peformed it's first succesful nuclear test.
4.4.3 Great Britain.
Great Britain was aware too, of the potential of fission of suitable heavy isotopes.They first fired up their own project (somewhere around 1940), but then in 1943, it more or less
was integrated into the Manhatten project.
It must be said that the British were the very first to actually fire up a project.
So, the British collected quite some relevant information. Short after WWII, there were
"certain reasons" as to why the British decided to get the weapon themselves.
You might expect some "help" or involvement from the USA.
However, it seems that the USA was rather reluctant to provide support in any way, in that phase.
Only historians (or politicians) can provide you solid details of why this was so at first.
Already as of '46, '47 this relaxed somewhat. However still no direct, active support from the US.
Since the British were now very determined to aquire the weapon, support facilities in the UK
were setup, and lots of detailed information was already in their hands anyway.
Their first test of a Pu based pure fission device, was performed in early october, 1952.
So, as of 1952, three nuclear capable states existed: USA, USSR, and Great Britain.
4.4.4 Other nations.
-In februari 1960, France performed their first test of a fission bomb as well, thereby aquiringthe status of a nuclear capable state.
- In october 1964, China followed with their first pure fission device, based on the
well-known implosion principle.
- Still later, some other nations joined the "club", like India and Pakistan.
4.4.5 Other remarks.
What was not mentioned in this subsection, that even before the "pure fission" bomb becamea reality, already physicists theorized about utilizing fusion as the main principle
for nuclear weapons.
The first test of a two-staged Thermonuclear device, was the US build bomb "Ivy Mike",
in November 1952.
In the decades that followed, we saw an avalance of nuclear tests, with at least 500
atmosperic tests, and nummerous other tests underground.
You do not need to be Einstein to understand that all those tests implied a huge exposure
to radioctive nuclides, to humanity and the environment.
Many reports exists, governmental, or from research facilities, or other expert reviews,
confirming this huge exposure.
Various studies have linked such exposure to life-threatening diseases.
But even without studies and reports, this is rather evident ofcourse.
5. Overview Nuclear capabilities per Nation.
Here, a simple and short overview will be presented on the present Nuclear capabilities of:UK, France, China, Russia, USA, India, Pakistan, and an attempt is made to say something useful on NK.
Israel will be left out from the discussion.
I still have a lot of work to do for this chapter.
5.1 Unclearity about counts of devices.
In general, treaties specify (among other things), the number of devices, and the count of "delivery systems"which can transport, or fire them.
For the nuclear devices themselves, it's rather evident that they may have the status of:
-In various stages of development.
-In final stages of development, nearing the operational status.
-Operational.
-Stockpiled (armed/disarmed).
-Variable explosive power, which hold for some special devices.
-The exact known mountpoint (in grenade, payload of rocket, torpedo, bomb).
-Part of a cluster of devices (like mirv of an ICBM).
-Set aside as Candidate for dismantling.
-Somewhere in the chain of development, operational/stockpiled, candidate for dismantling, dismantled.
-Dismantled, or in progress of dismantling, to make them fully unusable.
-Dismantled, or in progress of dismantling, but never to make them fully unusable.
-Originated from a friendly nation, but stored (operational/stockpiled) at this particular Nation.
This does not neccessarily obscure the counts of nuclear devices, but it certainly makes it harder
to exactly distinguish the "Operationals/Stockpiled" from all the rest of the devices.
This would hold for Nations which agreed to some treaty of some sort.
The obscurity actually really exists for Nations which did not adhere to any treaty at all.
You might agree that it is not possible, on a Global scale, to accurately specify the number
of nuclear devices. Likewise, it is not possible to accurately specify the the number of
"Operationals/Stockpiled" number of devices.
An estimate is the best we can do.
5.2 Main current nuclear weapons of the Russian Federation.
5.2.1 Introduction.
The largest number of "operational/stockpiled" nuclear weapons can be found in the Russian Federation.It's very difficult to accurately describe the full operational status of
"all domains" in the armed forces. For example, some Navy vessels seem to have a
"reduced operational status". But that's not unusual for NATO vessels as well.
But, Russian military budgets are considered to be quite tight in comparison to the US.
Nevertheless, the last 10 years (or so), core parts of the armed forces
experienced a massive upgrade. This holds too for nuclear devices and delivery systems.
Enormous "progress" was made, and ongoing, in e.g. fighter jets (e.g. Sukhoi Su-57 PAKFA),
ballistic missiles (e.g. RS-28 Sarmat), cruise missiles (e.g. Kalibr, Zircon),
new frigates (e.g. Gorshkov-class ), almost unbeatable SAM missiles systems (e.g. S400, S500) etc..
Contrary to new systems, older systems will be "refurbished" too, like the older Kirov-class battlecruisers
which presumably will be equiped with lot's of new detection systems, and armament (including the Zircon).
It's a tiny bit strange. I have some difficulties in seeing all the new stuff, and all upgrades, and
to reconcile that with "tight budgets" (but still somewhere around 70 - 100 billion $).
So, strangely, it probably still all fits in the bugets.
But it's also true that Russia is a large exporter of arms (like selling fighter jets etc..).
Ofcourse, the cold war and arms race from 1945 up to about 1989, was a main driving force.
I will avoid politics as much as is possible, but in later years (later of 1089):
- The occasional movement of some former Sovjet states towards Europe and NATO, must have constituted
a certain threat to Russia.
- Also, the placement of NATO Anti Ballistic Missile (ABM) systems, presumably to counter Russian missiles,
at various locations in Eastern Europe and at various other locations, likely triggered the Russian Federation
also in developing advanced weapon systems.
Just after 1991, the "states" Belarus, Kazakhstan, and Ukraine shortly inherited nuclear weapons,
as a result of the Soviet Union’s 1991 collapse. However, all weapons were returned to Russia.
In effect, all is stored now, in what is now know as "The Russian Federation", or simply Russia,
which largely looks like the former Sovjet Union, minus a few of seperated Nations.
There is a strange trend, seen with Russia, and to a lesser extend with China, to build
absurdly large ICBM's. For example the Chinese Dongfeng 41, but that absolutely, certainly
holds for the new Russian RS-28 Sarmat.
Especially the latter is simply a Doomsday device. No nonsense here. It's estimated that this missile
may have 10 *really* heavy nuclear warheads in MIRV, or up to 20 lighter nuclear warheads in MIRV.
Ofcourse, some NATO partners have ICMB's too using warheads in a MIRV configuration,
however, Russia's RS-28 Sarmat (per missile) is really much more devastating.
This machine will soon be operational, maybe as of 2019/2020.
Mind you, there already existed a large range of large ICBM's like for example the RS-24 Yars.
Below we will study most of those missiles.
Maybe you believe that a defense against those machines is possible, like "anti missile" missiles,
but presently, that is definitely not guaranteed, even if only a limited number of Sarmat's are launched.
The "Anti-Ballistic Missiles" (ABM) maybe succesfull to certain ballistic missiles, but those with
certain "detection evasion capabilities", or "irregular maneuvering capabailities",
are too difficult to target.
In the sections below, we will see the following selection of modern nuclear arms of the Russian Federation:
-Current ICBM's (landbased, not submarine launched SLBM's)
-Current Long range (strategic) bombers
-Current SSBN's (submarines) and SLBM's (missiles)
-Current Nuclear capable cruise missiles
5.2.2 Current ICBM's (landbased, not submarine launched SLBM's)
with Full Operational status:
Let's investigate the following land-based ICBM's:| Name: | NATO designator: |
| RS-24 Yars | SS-29 |
| TOPOL classes ICBM's | SS-25 / SS-27 |
| R-36M / R-36M2 Voevoda | SS-18 Satan / SS-18 Mod.6 |
| RS-26 Rubezh | SS-X-31 / SS-X-29B - derived from SS-29 |
| RS-28 Sarmat | SS-X-30 or "Satan 2". |
A few more classes still exist, but the list above constitutes the truly current (live) delivery systems,
having full support in the Russian Federation.
⇒ RS-24 Yars (SS-29)
Fitted for launch from Silo, as well as for Mobile launch trucks.Generally viewed as the followup (modernized version) of the Topol-M / SS-27.
However, modern Topol class missiles still form a core of the Ballistice force, and it's likely that
they will hold that status for quite some time to come. For the last statement: some reports say differently.
Introduced in 2007, and it reached a production status around 2010. However many adaptations seem to have
been done after 2010, and quite some tests have been performed too in the period 2010-2017.
It's a 3 stage missile, using Solid fuel.
It's a MIRV capable missile. Likely to be in the configuration of 3, 4, up to 6 warheads. Reports of specifying up to
10 warheads, are generally questioned. But, "4" is likely to be the default number of warheads (100-300 kT).
The missile is currently a long-term piler in the Deterrence policy.
Range: around 12000 km
Accuracy (CEP): very high. Probably 150 m.
Number in operation: likely to be around 108 systems.
MIRV capable: likely to have up to 4 (or up to 6) warheads in the class 100-300 kT.
Irregularities are implemented in the final flight paths of the warheads (maneuverable reentry vehicles), and are intended
to make interceptions practically impossible. It's possible that "Avangard" gliding techology is used.
Speculative content:
- Since RS-24 is the current state of the art, and most proven ICBM with MIRV, it's likely the numbers will grow larger
than the often estimated number of 108 systems. Note that this is a speculative statement.
- A derived variant of the warhead exists, build for the RS-26. This missile may circumvent/bypass the INF agreements
since the missile may have been classed as long-distance ICMB's, but it is actually intended for medium range operation.
Below is a YouTube Clip. It's unknown in how far the content of this clip is fully accurate. However, I think it is quite accurate.
New Yars ICBM will beat any anti-missile defence
⇒ Topol classes ICBM's (SS-25 / SS-27)
Two main variants exist:The first one: RT-2PM Topol (or SS-25 sickle).
The follow-up: RT-2PM2 Topol-M (or SS-27).
The first Topol entered service in 1988 as fully operational. The first concepts and designs go back
as early as (probably) around 1977.
The first test launch of the Topol-M was 1994.
The RT-2PM2 Topol-M (or SS-27) can be considered to be the father of the RS-24 Yars.
But modern Topol class missiles still form a core of the Ballistice force, and it's almost certain that
they will hold that status.
Recent testlaunches of the SS-27 seems to confirm this.
Both are fitted for launch from Silo, as well as for Mobile launch trucks.
The RT-2PM Topol is generally considered to be the first mobile (Mobile launch trucks) ICBM.
The SS-25 is considered to be a single (large) warhead weapon. The SS-27 is very comparable to the SS-29 (RS-24),
because it's MIRV configuration of 4, or up to 6, warheads.
Some reports also attribute sophisticated "maneuverable re-entry" capabilities in the final flight paths.
This is supposed to be implemented after seperation of the warhead(s) from the carrier missile (third stage).
Range: around 11000 km
Accuracy (CEP): high. Probably 300m - 900m, or better.
Number in operation: likely to stay around 170 systems. This holds primarily for the SS-27.
Number of warheads:
SS-25: likely to be configured for one large warhead (800 kT or larger), but it could be modified for MIRV too.
SS-27: likely to be MIRV capable: likely to have up to 4 (or up to 6) warheads in the class 100-300 kT.
The numbers for the warheads, vary over reports and articles. Sometimes, the Topol-M is listed
as a single warhead weapon too (non MIRV capacity).
However, it's very likely that the SS-25 uses one large warhead, while the SS-27 is per default configured for MIRV.
⇒ The modern R-36 variants (R-36M / SS-18 Satan and R-36M2 Voevoda / SS-18 Mod.6)
The "R-36M" or NATO qualifier "SS-18 Satan" is a monster. You can say no less than this.The collection of R-36 variants, is a large family of missiles, some of which were build end '60's and early '70's.
However, the modern variants still form an extremely powerful component in the Russian nuclear force.
The '60's and early '70's machines, have been phased out oufcourse, and replaced by newer ICBM's.
Although the history is very interesting, even more interesting are the incredable capabilities of the "ORB"
variants, which could even "stay" in orbit for a certain amount of time.
Many variants were typed by the qualifier "MOD" (model) like MOD4, MOD5 etc..
Today, still some modern R-36 variants form a core of the Russian nuclear deterrence, and the specs are awesome.
Well, I mean "awsome" in a depressing tone, since the payloads are enormous. Those modern R-36 variants
are the most powerful ICBM's today, until the new "RS-28 Sarmat" will be fully operational.
Two main variants are in operation:
-The R-36M, or also known as SS-18 Satan (NATO name).
-The R-36MUTTKh and R-36M2 variants.
The SS-18 Satan has an enormous payload (or throwweight). It is believed by most sources, that it may
be configured with one 20 MT (megaton) warhead, or, it can be configured for MIRV, where various
numbers of warheads are published by various sources. Some report for even over 14 warheads.
In MIRV configuration, I find a (sort of) consensus of a possible configuration of 10 warheads of 0.5 MT,
or even well over 0.5 MT, which may form the payload.
SS-18 Satan:
Launch: From silo only.
Range: around 11000 km
Accuracy (CEP): high. Probably 300 - 400 m.
Number in operation: Once a large number. Today, or in the near future, it will make place for the newer RS-28 Sarmat
Most sources say that today at least 40 R-36M's have an operation status.
MIRV capable: likely to have up to 10 (or up to 14) warheads in the class 0.5 MT - 1MT.
Thus: Just 1 missile is thus capable of destroying a nation of the size of Germany or Great Brittain.
The machine can also be configured to have an absurd payload of a device having an explosive power of 10MT or even 20MT.
Below is a YouTube Clip of a test launch of SS-18 Satan.
Launch of a R-36M / SS-18 Satan
⇒ RS-26, Rubezh/Avangard/Frontier (SS-X-31 / SS-X-29B - derived from SS-29)
This new machine is largely based on the RS-24 Yars, as it uses (only) the first two stages of that missile,and it seems to use adapted warheads of the Yars, as well.
It (sort of) "hovers" in the "grey area" of being classified as an ICBM, or as an "Intermediate Range" nuclear missile.
Treaties specify an ICMB, if it can reach a distance over 5500km. Interestingly, the RS-26 have been tested to reach
over 5800km. Thus, it's an ICBM, according to the INF specifications. However, it's substantially smaller
than other current Russian ICBM's, and it's typical targets seem to be within a radius of 5500km.
In my opinion, it's rather tempting to say, that this devices is clearly ment for "Intermediate Range" purposes.
One should notice, that if any note or article says that a device might be a treaty breach, that a crosscheck
with other sources, is pretty much mandatory.
Everything on the RS-26 is somewhat downsized. The mobile truck is smaller, and so is the missile itself (compared
to for example RS-24 Yars). The smaller dimensions has certain advantages, as easier to maneuver, faster etc..
It's excusivly for trucks only, and it's likely that no silo will house them.
Warheads themselves evolve too ofcourse. It's rather likely that the newer ICBM warheads might use newer tactics
like using a sort of "surfboard" irregular gliding path towards their targets.
This manner of speaking must not be taken too literally, since the speeds of warheads is enormous.
But gliding, evasive and seemingly "irregular" paths, is a true new feature of ICBM warheads.
There is one type of RS-26, but it is also often referred to as RS-26 Rubezh or "Avangard", where the latter term
is used to referr to the "gliding" technology of warheads.
The same sort of thechology is used (or will be used) on the RS-28 Sarmat or Satan 2.
Launch: From trucks only.
Range: ???? A large distance for this missile seems to be 5800km
Accuracy (CEP): very high. Probably in the order of 100m.
Number in operation: not known. Number planned: likely to be high.
MIRV capable: likely to be similar as RS-24 Yars, thus up to 4 (or up to 6) warheads in the class 100-300 kT.
The YouTube Clip below, is somewhat "fast" and possibly confusing, but later on, it shows some details on the RS-26 Rubezh.
RS-26 Rubezh
⇒ RS-28 Sarmat (SS-X-30) or "Satan 2"
It may certainly be viewed as the successor of the R-36M or SS-18 Satan missile.One should keep a note like this, cool and business-like, but the RS-28 Sarmat, is a missile with an absurd
over-capacity. One such missile alone, is able to completely flatten Germany, or France, or comparable region.
Having seen the devices above, like the RS-24 Yars, Topol class, RS-26 etc.., one might wonder on the neccessity
of the RS-28 Sarmat, or, in other words, what inspired the Russian Federation?
One reason might be to have the certainty that the "Deterrence works, no matter what..".
Indeed, if a number of Sarmat are fired, it will always hit, and I believe no presently existing shield (like ABM),
will work.
It is probably fair to say that Western / NATO Anti-Ballistic Missile missiles "progress",
(at least partly) triggered the Russians too, to create the RS-24 Yars and RS-28 Sarmat.
But..., now there is the problem of absurdly large and efficient missiles. Those don't go away soon.
It's expected that the R-36M / SS-18 Satan will gradually be phased out, as the Sarmat slowly get's fully
operational, and the number will grow to the desired force.
It is believed that the payload may exist in up to 16 smaller warheads (hunderds of kT), up to a lower
number of MT class warheads, and theoretically maybe even larger warheads.
Some reports speak of 20, to even 24 smaller warheads (100 kT class).
The "Avangard" warhead gliding technology is implemented with the Sarmat. However,
the missile lends itself for certain selected mixtures of large- and smaller warheads.
Launch: From silo (for now).
Max Range: around 14000 km - 17000 km
Status: Most tests completed. Not in full operation yet.
Accuracy (CEP): high. Probably less than 100m.
Number in operation:
-Unknown, but the first batches will likely produce around 50 missiles, in operation after 2020.
-Maybe the number goes to > 100, depending on START agreements, in conjunction with the number of other new types of ICBM's.
MIRV capable:
- likely to have up to 16, or 20 warheads in the class 100kT - 300kT (*).
- or a lower number of Megaton class warheads.
- mixtures of lower and larger warheads.
Evasion technology: Warhead "gliding" evasion technology.
Probably implemented: FOBS which mean that warheads can stay in orbit, until triggered to start the descend.
Note: I do not dare to provide a link to a YouTube clip, since some clips seem to show the R-36M / SS-18,
or just components like a stage test, instead of the full "real thing".
(*): Please remember that "Fat Man", the bomb thrown at Nagasaki in WWII, was about 20 kT.
This concludes the small survey of modern Russian ICBM's. Next, we will go to strategic bombers,
submarine launched nuclear weapon systems (SLBM's), and nuclear cruise missiles.
5.2.3 Long range bombers:
For interceptors, fighter jets, fighter/bomber multirole planes, then names as "Sukhoi" and "Mig"are most prominent in the Russian Airforce, and Naval forces.
No doubt that many of their later models must be placed in the air-superiority classes.
Indeed, also bomber- fighter/bomber, for short- and medium range exist, and quite a few have
capabilities to carry nuclear payloads (like cruise-missiles).
For long-range (strategic) bombers, we will touch upon the Tupolev Tu-160(M2), Tu-95,
and Tu-22 bomber planes.
⇒ Tupolev Tu-160 ("White Swan") and the updated Tu-160M2
The Tupolev Tu-160 machine, is operational since 1986.Around 1998 it momentarily seemed, that upgrades on the Tu-160 would be scrapped. But as data shows,
upgrades have indeed been carried out. The very latest (completely overhauled) version is the Tu-160M2.
Production will start as of 2018. This section deals mainly on the Tu-160.
This "Concorde lookalike" plane is supersonic, with a max speed of Mach 2, or slightly above.
It's considered to be extremely capable, in delevering nuclear weapons. Especially, it can carry
up to 12 Kh-102s nuclear cruise missiles, of which it is believed that the range of such missile
is well over 2000km.
One of the original cruise missiles, was the Kh-55 cruise missile. A conventional and nuclear variant existed.
The variety of Ks missiles, in time, is indeed rather large too. The conventional Kh-101 is an upgrade to the
conventional Kh-55. The Kh-102 is the latest cruise missile with a nuclear warhead.
It's a subsonic air-launched cruise missile, believed to use a low-altitude operational flight.
As already mentioned, it's believed that the max range is over 2000km (some reports say "well over 1000 miles").
It is further very likely that the modern Kh variants have a form of stealth implemented, like using radar
absorbing materials.
Modern guiding systems, or programs, make the missile very accurate, as well as it seems possible that
the missile is even capable to re-select another target, in flight.
The Tu-160 is ofcourse also usable for using gravity bombs, however, the standard cargo bombarrays
are designed for the Kh series.
The latest upgraded subtype is the Tu-160M2, which is very close to operational status (early 2018).
The history of the Tu-160 is very much linked to the relation of Russia and the Ukraine.
At a certain point before 1991, the Ukraine had (around) 19 Tu-160. However, since the breakup of
of the Soviet Union, the Ukraine was not really able to support this fleet.
In 1999, Russia bought (around) 8 Tu-160 back, and the remaining Tu-160 were neglected or cut up.
The number of fully operational Tu-160's (right now) in the Russian Federation is not fully clear.
It seems that around 2008/2009, 16 operational Tu-160's are in service at the Russian Federation.
It's realistic to say that the number of planes today, due to re-instates, is somewhat higher: maybe 24.
It seems rather obvious that the new Tu-160M2, will see a certain production rate, however,
I have not found any realistic estimation in terms of numbers.
However, I have little doubts that this effective bomber, that is the rebuild Tu-160M2 (as of 2018),
will be a piler in the triade of deterrence of the Russian Federation.
Also, NATO will see it more often along the coastlines, near the European borders, replacing the Tu-95.
One noteworthy point is this: using cruise missiles, the Tu-160 is able to carry out a remote strike,
and even a remote nuclear strike. This is different from a bomber using gravity bombs, which must penetrate
into the target area.
Specs:
Max speed: mach 2+
Max Range: at least 12000 km (assumed with 6 Ks missiles)
Ceiling: 16 km
Engines: 4 × NK-32
Overhaul: the Tu-160M2 is a complete overhaul in terms of electronics, control systems etc..
Delivery:
-max 12 x Kh-101, or Kh-102, or other Kh serie of missile.
-large range of different gravity (free fall) bombs.
Numbers: At least 16 Su-160. Maybe 24. The Upgraded Tu-160M2's, as of 2018, will be added to enter service.
Some unconfirmed sources refer to a future number of about 50 Tu-160M2's, as of 2023.
Note: the "total" range is the true max distance. The "combat" range is often considered to be considerably less
than half of the max range, but other interpretations are used too.
There are quite a few (YouTube) vids, showing the Tu-160 in action, like deploying cruise missiles.
But it's rather unethical to refer to them in this note. However, the following vid (no violence) gives a good
view of it's overall shape and dimension: Flight of the original Tu-160 White Swan.
The second vid clearly displays Russia's commitment on the new, completely revised, Tu-160M2.
VIDEO: Flight of Tu-160 White Swan.
VIDEO: Russia's commitment on the Tu-160M2.
⇒ Tupolev Tu-95 (Bear)
Able to cover very large distances, with a large payload, characterizes some subtypes of the "Bear".This was the "typical" cold war long distance bomber. But it still has an active role,
and will certainly be around for quite some time to come.
This plane is not a "jet", but uses 4 turboprop engines with contrarotating propellers, enabling the Tu-95
to reach a max speed of about 925 km/h, which is comparable to a civilian airliner jet.
In time, a large number of variants existed. For example, a naval patrol version is typed the Tu-142.
The first Tu-95's are from 1952. However, many upgrades have been implemented, and almost all planes
today, are not build earlier than the '90's.
Many were decomissioned, others were upgraded or rebuild for other duties.
For example, the Tu-142 series, have specialized functions, like naval patrol, or anti-sub duties, and cannot
as such be counted as the typical long-range strategic bomber.
Most "military" related sources, say that nowadays the Tu-95MS (the bomber), and Tu-142 long range maritime aircraft,
are the only active machines in service today (apart from a few very specific versions).
For the true bomber role planes: once it was meant to carry a large amount of gravity bombs.
However, some variants (e.g. H series) were rebuild, to carry and launch the Kh cruise missiles too,
just as the Tu-160 is able to do so.
So in general, many Bears (Tu-95MS) are capable to carry the same variety of Kh cruise missiles,
as described in the section of the Tu-160 above.
However, this does not hold for the Bears with specific roles (like naval/anti-sub Bears).
The Bear was the "typical" bomber to cruise along Western coastlines (often Europe,
and in a few cases, North America too), but such patrols (Europe) seems more and more to be given
to the Tu-160.
It's enormous total range of nearly 15000 km, will garantee that it will have a role for years to come.
Just like the Tu-160, the long-range cruise missiles enable the Tu-95 to execute remote strikes,
conventional and nuclear. It does not need to penetrate the target area's.
Note: the "total" range is the true max distance. The "combat" range is often considered to be considerably less
than half of the max range, but other interpretations are in use too.
About "absolute" numbers of operational Bears today, there seems to be some "fuzzyness", at least, to me.
Again, since the breakup of the Sovjet union, quite a few Bears returned to Russia, while others
were neglected or cut up. This holds for example for Bears once stationed at the Ukraine, and Kazachstan.
Specs:
There is no single set of specs, applicable for all Bears that existed once.
The Bears (subtype H type, or Tu-95MS) equipped for the long-range strategic role, the following holds:
Max speed: fastest Bear's reach 925 km/h.
Range: near 15000 km (as often reported, but no data in relation with payload)
Ceiling: 13.5 km
Engines: 4 × NK-12
Delivery: Long-range bomber Bears: max 6 to 8 Kh series of missiles.
Numbers:
-Likely around 32 Tu-142 series, (including some specialized versions Bear's) in service at the Russian Navy.
-Several numbers of Tu-95MS are distributed at various bases (like Engels base etc..). I have no concrete numbers,
but some sources refer to about close to 40 Tu-95MS as an overall number, including close-variants of this subtype.
This suggests a total number of 72 Bears in operational status. However, Reliability of this data is "Low".
It seems rather save to assume to total of (at least) 55 operational Bear's (Tu-142 + Tu-95MS) in total.
There are quite a few (YouTube) vids, showing the Bear, and some also display it in action.
The following vid (no violence) gives a good overal view of it's overall shape and dimension.
VIDEO: Intercepting a Bear at Alaska.
⇒ Tupolev Tu-22 ("Backfire")
(Sometimes also referred to as Tu-26).The first one appeared in 1969, quite rapidly followd by some variants in the years that followed.
Although a supersonic bomber, those first generations never could quite convince military experts.
The Tu-22M3 entered service around 1983. This one was a complete overhaul and it shared nothing from predecessors,
exept it's overall external "looks".
Finally, it was indeed qualified as a capable bomber, although the max range (and combat range)
still remained a bit feeble, compared to what's understood to be real long-range bombers,
like the Tu-160 and Tu-95MS bombers.
One important designated function, especially in the '80's, was probably an "anti-carrier"
role, mainly due to the standard armament of Kh-15 or Kh-22 cruise missiles.
It was never directly displayed as a nuclear bomber, but it has the capacity to assume that role.
Certainly the refitted Tu-22M3 will have arrays to house the nuclear Ks series of missiles.
The max range of about 7000km (or combat range of about 2500km) may just be enough, to put it in
the long-range bomber class.
Since 2015, the bomber did quite a few sorties in Syria, mainly using gravity (free fall) bombs.
Over all those years, it seems likely that well over 500 Tu-22x machines were build. Most are gone
by now. But it's not obsolete today. It's certain that the Russian Federation wants to keep a core
fleet of such planes, probably in the order of 100, and modernize those Tu-22M3's once again.
Specs:
Max speed: Mach 1.88
Max range: 7000km (combat range over 2500km)
Ceiling: little over 13 km
Engines: 2 × NK-25
Number: core fleet of at least 100 upgraded Tu-22M3
Note/Correction: in a former version I came up with a total of around 30. It now seems more likely to be
in the order of 100 Tu-22M3's. This comes from more carefully inspecting various sources.
Delivery:
-Large range of gravity bombs, like FAB-250, 270, FAB-1500, or specialized Naval ordonnance.
-Anti-ship cruise missiles Kh-15, Kh-22, Kh-55 in internal bombarray.
-External mountpoints for Kh-15 class of missiles (typical 3).
There are quite a few (YouTube) vids, showing the Tu-22M3 in action, but it's rather unethical to
refer to them in this note. However, the following vid (no violence) gives a good view
of it's overall shape and dimension: Taxi and takeoff Tu-22M3
VIDEO: Taxi and takeoff Tu-22M3
Remarks:
(1). Ofcourse, many large planes were skipped in this section, like Heavy Transport-, Reconnaissance planes etc..
Only "strategic (long-range)" bombers were sketched.
(2). Planes which are almost obsolete, or which do not play any significant role anymore in the strategic theater,
were skipped.
(3). Quite a few Mig and Sukhoi fighter/bombers exist at the armed forces in Russian Federation. Most of them
can cover a distance which can be typed as "medium-range".
I like to discuss them in the section which covers tactical weapons.
Also: the central theme in this note is: delivery systems which have nuclear capabilities.
5.2.4 Current SSBN's (subs), SLBM's (missiles),
and nuclear long-range drones like Status-6
The Sovjet Union, and later the Russian Federation, have produced a dazzling array of Submarines,conventionally- and nuclear powered. You can further make all sorts of divisions in types,
like "ballistic missile carrier", or "attack submarine" etc..
You may encounter many NATO designators for all such "older" types, like Echo, Whiskey, Charlie,
Delta, Alfa, Sierra etc.. etc.., when bowsing through various Military/Naval websites.
For us, only the later models are relevant, of which we can be sure that they will remain in service
for a relevant period of time. Also, I only focus on Subs which (under regular service), are equipped
with nuclear armament, like SLBM's, or cruise missiles, or torpedo's etc..
The table below, simply shows the subs which I think are the most interesting. Ofcourse, many older
types are still in service.
So, please remember that the table below, and the discussion which follows, *only* deals on more recent
and modern Submarines, skipping the older ones (like before 1985).
I like to stress the fact, that the discussion below, only deals on modern subs (say as of the '90's),
which uses modern technology, with a strongly reduced noice profile, and carry nuclear armament.
As a completely different class: There exists various Autonomous mini subs, or drones, able to carry
nuclear devices. Most notable member is the "Status 6" or "Poseidon" (unmanned) autonomous device,
which is quite similar to a submerged ICBM, and is likely to carry a large thermonuclear device.
So, in particular, I like to spend a few words on the following Subs:
| Project: | Nato Name: | Total/planned: | Currently operational: | Remark: |
| Projects 955/955A/955B | Borei classes | 14 | 4 (over several subtypes) | SSBN - main task: SLBM carrier |
| Project 941 | Typhoon | 6 | 2 (probably 4 decommissioned) | SSBN - main task: SLBM carrier |
| Projects 971 (I/U/M) | Akula classes | ? | 14 (over several subclasses) | main task: nuclear Attack sub |
| Project 885/885M | Yasen classes | 8 to 10 (?) | 2 | main task: nuclear Attack sub |
| Status-6/Poseidon | Kanyon | ? | ? | long-range Autonomous Drone (submerged ICBM) |
| Belgorod Project 09852 | Modified Oscar II | ? | ? | Special Ops and Launch platform Status-6 |
The term "SSBN" refers to a nuclear powered submarine, which is capable to launch Balistic missiles.
Those missiles carry one or more nuclear warheads. Almost always, there are multiple warheads involved
per missile.
The term "SLBM" is short for "Submarine Launched Ballistic Missile", thus referring to the missile itself.
⇒ The new Borei (Borey) class sub (Projects 955/955A/955B):
A subject like enummerating operational subs, and those scheduled to enter service in the near future,probably does not look as an especially difficult task.
However, I found that finding consensus among articles, or analysts, is not always easy.
Currently, the Borei class (Borey class) form the latest subs in the Russian Navy.
The first vessel commenced it's sea trials in June 2009.
There are probably three projects, defining three Borei classes.
It started out with Project 955. Followed later by Projects 955A and 955B.
These specs are also often referred to as Borei I, Borei II and Borei III.
Three vessels of the Borei 955 class (at the time of writing), were indeed constructed and have
an operational status.
The fourth one, is just finished, and was build according to the 955A specs (Borei II). Here some further
technical innovations are implemented, like further reducement of the noise profile.
It seems that Borei III might be delayed, or (partially) posponed, or even abandened. This is not fully clear
at this moment. Considering the policies of the Russian Federation, it might also be true that the Borei III
is back on the drawing board again, or that selected features will be implemented at Borei II vessels
which will be build after 2023.
Although the Borei I and II classes have a similar name, there are substantial different "specs"
between the classes, like a strongly reduced noise profile for the II class.
A consensus between analysts seem to exist, that in total 14 Borei class vessels will be delivered, where
most of them are of Borei 955A (or of the Borei II) type. The first 3 delivered, were build according to the
original 955 specs.
It's planned that 8 Borei's will be operational in 2022, while the rest will follow after 2023.
→ All of them will carry the "Bulava" SLBM (SS-N-32) where the first 3 vessels have 16 launchtubes,
and the later vessels probably will have the same number of launchtubes.
Some reports or analyst maintain however, that the later Boreis's will probably have 20 launchtubes.
It seems to me that 16 is the number for future vessels as well.
→ All of them will also be equipped with the SS-N-15 anti-ship/anti-sub torpedo's, which may carry
a 20 kT nuclear warhead.
| Project: | Class name: | Total number planned: | Currently operational: |
| 955 | Borei I | 3 | 3 |
| 955A | Borei II | 11 | 1 |
| 955B | Borei III | posponed/abandened/under study? | 0 |
The Borei seems to be a replacement for the Delta class subs. Most analyst name the Typhoon class subs too
as to be replaced by Borei. I am not so sure of this, which will be explained when we will take a look
at the Typhoon class subs.
These subs are capable of diving to at least 400m, and have a submerged speed of about 45 km/h.
The crew consists of about 107-130 members, and it's length is about 170m, with a displacement of around 24000 ton.
The Bulava SLBM:
-NATO name SS-NX-30 or SS-N-32.
-Up to 6 to 10 warheads in MIRV of 100-300 kT.
-Maximum distance of 8500 to 10000 km.
-Evasive maneuverability capability.
-CEP: about 250 m.
-Below is a YouTube Clip of 4 test launches of Bulava's, from the first operational Borei vessel.
4 test launches of Bulava's
-Below is a link to a nice picture of the architecture of a Borei II vessel:
Schema of the Borei II (i.redd.it)
⇒ "Status-6/Poseidon/Kanyon" and Delivery systems:
Ofcourse, the new Borei class of subs are real. They exist ofcourse.These are machines with great capabilities and an enormous nuclear fire-power.
But if we consider some new deep-sea drones, which are supposed to exist, or which the Russian Federation
is developing, I cannot say anything less than that we are entering a "misty" territory.
One name of a large unmanned drone, which is often heard, is "Status-6", or also called "Poseidon", or also known
by it's NATO identifier "Kanyon".
You may doubt it's existence, as many folks do. I personally had strong reservations too.
Especially, the first specs of Status-6, which surfaced a few years back, were nothing less than abnormal.
Basically, the first specs which came out (or were rumoured) were something like this:
-Unmanned large underwater Torpedo/Drone or UUV.
-Cruise depth of around 1000m, cruise speed of 100-185 km/h.
-Range many thousends of miles (similar to a submerged ICBM).
-Nuclear propulsion, indeed making large distances possible.
-length of about 24m, width about 1.6m. Probably fired from a specialized/modified large Sub.
-Warhead: in the order of 100MT thermonuclear warhead.
-Possibly even using a Cobalt mantle, making it effectively a Cobalt bomb.
The "term" torpedo, would be ill-chosen. A description as a "autonomous robotic submarine" would
probably fit it better.
The listing shown above, does not seem to be very realistic. 100MT warhead is really very heavy, and an undersea
drone to export it over vast distances, seems not realistic. Also, what about navigation? At 1000m depth, it sure
is not easy to follow a precise trajectory, unless it surfaces once in a while, to establish position and correct
it's course. Also, the seafloor is not exactly flat and smooth at all places, etc.. etc..
As another thing, if the above listing would be true: such a device would be unmanageble. Once fired, it goes,
and nobody can do anything about it. Secondly, it would be able to contaminate a whole continent.
It simply does not make sense, not even for the "darkest mind" around.
However, you could simply say that the same holds for the current collection of ICMB's, existing
in the East and West.
If I say "not realistic", does not mean that it would not be "feasable".
Not withstanding the fact that those specs listed, seems to be unrealistic, in March 2018,
Pres. Putin addressed his Nation and also mentioned the existence of unmanned, submerged nuclear drones.
This changed matters for me, and probably for other folks too, and his speech really confirmed the existence
of undersea drones carrying large nuclear devices.
Indeed, I take the words of Pres. Putin in such context, very seriously.
Having long-range drones with a nuclear device, still is another story from the "100MT continent killer".
It could simply mean a submerged drone, rather equivalent in capabilities as a hypersonic cruise missile
like a Zircon or Bhramos, which might knock out a carrier fleet.
There seems not to exist easily accessible information about Status-6. There are however, some figures
easily obtainable from the Internet, which shows Status-6 in some detail. You can find them yourself,
using Google.
Unfortunately, I cannot show pictures of vessels and devices and stuff, since I cannot know which
of them are protected by copyrights, unless they are confirmed to be in the Public Domain.
It's true that the affairs around Status-6, resembles the situation in the early '50's of the former century.
At that time, the Sovjets had developed the T-15 nuclear torpedo, carried by the Sub classified as project 627.
This enormous torpedo was intended to strike US ports and shores. The sub itself, was more like a machine
dedicated and constructed around the launchtube. This one really existed.
In a way, it seems that history repeats itself when referring to Status-6.
From this perspective, and remembering Pres. Putin's speech, and the fact that I am personally
convinced that the Russian Federation wants to be able to have nuclear deterrence "no matter what...",
makes me believe that Status-6 is indeed the longrange submerged equivalent of a large ICBM.
However, even if the 100MT turns out to be (the more realistic) warhead of 20MT, it still would
be a formidable weapon, in terms of pure destruction. That would even still hold for 10MT.
Note: the largest nuclear device ever produced, was around 50 MT (the Sovjet bomb "Tsar Bomba", 30 october 1961).
This fact makes the number of 100MT, even more unrealistic.
However, if Cobalt and/or Uranium mantles are used, with the pure intention to contaminate the larger part of
a continent, I really cannot call it a weapon anymore. I think you know what I mean here...
Because the nuclear firepower of the Russian Federation already is enormous, when considering their regular
ICBM's and SLBM's, the existence of Status-6 is utterly useless.
But it's here, and development/construction would make it an operational member in the nuclear arsenal
as of 2020, as I see it.
About the numbers, I have no clue. Given the fact that "special mission" subs exist, which seem
to be able to fire 4 to 6 of such "torpedo's", I fear the worst.
I apologyze for a certain degree of possible speculative content in this section. But that is just
the result of knowing that a certain device exist, while many parameters are simply unknown.
Additions at July 2019:
(1): It now seems that a modified Oscar II sub, a vessel probably called the "Belgorod", or Project 09852,
might function as a Special operations Sub, including the task as a launch platform for Status-6.
Please see the section on the "Belgorod / Project 09852" below.
(2): Several recent (but scarce) articles have studied Status-6, for as far as is possible
for an undisclosed device. A commonly listed explosive output for Status-6, is 2 Megaton,
which is much more realistic compared to the figures above.
However, (1) and (2) are not exactly proven, but nonetheless seem to be realistic assumptions.
⇒ The Typhoon class Submarine (Project 941):
Note: In Russia, this class is called the "Akula" class, while the NATO designator is "Typhoon".Since a later hunter/killer Sub is called "Akula", I will keep calling the Project 941 subs,
as the "Typhoon" class.
These were the largest subs ever build. They became gradually operational over the years in the '80's.
In total, 6 were build. Each had 20 launching tubes for the R-39 SLBM's (SS-N-20 Sturgeon).
It's certainly true that in those days, they represented an awesome and powerful nuclear force.
There were also famous for their high degree of stealth and low noise profile, as measured from
the technical perspective of those times.
They operated often in Icy seas, and their enormous strength was proven constantly. I think it's
hard to find any match for the toughness of these machines. There isn't any.
Very cool are also the two large "escape chambers", on both sides, for 85 crewmembers each.
To characterize those vessels: length: 175 m, max width: 23 m, max speed: 27 knots,
crew: around 160, Submerged Displacement: 48000 tons.
It's true that the series are candidates for decommission. In fact, 3 or 4 of them *probably* already
have been decommisioned.
The R-39 SLBM's have been decommissioned too, and have no operational status anymore.
However, the two remaining vessels have, so I believe, a sort of reduced operational status.
Assuming that there still exists two vessels, then one of them, the "Dmitriy Donskoy", is
still "near" an operational status.
Ofcourse, the operational costs of such large machines are extremely high. However, the requirements and needs
of the Russian navy for the near future is not clear, and as said before, they might get other duties,
different from the Ballistice Missile carrier as they once were.
It's commonly believed that the current operational Typhoon is sometimes used as a test platform
for new SLBM's like the Bulava.
However, to completely refit them for the "Bulava" SLBM (SS-N-32) does not seem likely, since that would
violate current treaties.
But, the value of treaties can be questioned nowadays, whether you believe that or not.
If indeed 2 Typhoon's are still around, then for the nearby future, a few possible scenrio's are:
-One vessel might be refurbished for other duties. One vessel might be frozen, and stay idle for some years.
-Both vessles will be refurbished for other duties (special ops, cruise missiles platform etc.. etc..).
-Or both vessels will be phased out since e.g. the modern Borei's are much cheaper to operate.
-A very cool picture can be find at the following link:
Schema of the Typhoon (www.hisutton.com)
-The following clip shows a Typhoon (Dmitriy Donskoy TK-208) in a recent Navy Parade (St. Petersburg),
as still alive. So, the largest and overall strongest sub ever build, is still in shape.
Navy Day in The Russian Federation (St. Petersburg)
-The following clip (10 minutes) gives more insight in these machines. It's quite obvious that
the Typhoon (Akula Project 941) absolutely is the largest, and strongest, submarine EVER build.
Typhoon - the largest submarine ever (Horizon)
⇒ The Akula classes of Submarines (Project 971):
The former two subs (Typhoon, Borei) are carriers of long-range SLBM's. These are weapons that fit intothe nuclear deterrence policy. However, they carry short-range nuclear devices too, like their anti-ship/anti-sub
torpedo's. See their specs in the former sections.
The Akula class is a real Hunter/Killer sub. This time, we see a sub which is especially designed to destroy
ships and subs of the enemy.
However, they carry intermediate-range nuclear cruise missiles too, extending their possible targets, which
thus might be located deep land inwards.
There exists 3 to 4 subclasses, a bit depending on how you look at matters. Each time, the newer subclasses
can be viewed as strong technical updates compared to the earlier classes.
However, the dimensions changed too with later subclasses (they became larger).
Before the '80's, people were quite right when they said that Russian subs were noisy, where the Western
vessels had a clear advantage over them. Since the second half of the '80's, that begun to change dramatically.
When the first Akula became operational, around 1986, the Western Navies and Intelligence services, were deeply
impressed by the stealthy features of the Akula class. Since the first one, the later subclasses performed
even better in noise reduction and other stealthy feautures.
To characterize those subs (Akula II and III): length: about 113 m, max width: 13.5 m, max speed is largely unknown,
but it is certainly above 32 knots, crew: around 70, Submerged Displacement: around 13800 tons.
All Akula subclasses have nuclear propulsion, and are believed to be able to reach astonishing depths.
For the Akula III, the max depth is estimated to be in the order of 600m.
Ofcourse, the first subclasses (Akula and Akula I) will not be build anymore, since better updates
have been commissioned (Akula II and Akula III).
The currently operational number of Akula's is not exactly known. Also, a few might have the status of being
overhauled, and a few others might have a reduced operational state.
To complicate this a bit further: At least one Akula (971I) was leased to India. At least one Akula (971M)
was reused for the initial Borei class.
I found consensus among most analysts, that 14 Akula's are currently operational.
That number is not exactly in line with my table below. But as it seems to me, really exact information
is not available in the public sphere.
The following table tries to illustrate the Akula classes and their status.
| Project: | Class: | Total number: | Currently operational: |
| 971 | Akula | 7 | 3 (4 decommissioned?) |
| 971I | Akula I | 6 | 6 |
| 971U | Akula II | ? | 1 |
| 971M | Akula III | ? | 1 |
Cruise missiles:
Traditionally, the first Akula's were equipped with 12 Granit (SS-N-21 Sampson) submarine-launched cruise missiles.
These have a range of about 3000km and use a single 200 kT warhead.
The fact that the last 8 years, the Russian Federation made enormous progress in "short/medium/long" range cruise missiles,
(whether in the sub-/super-/hyper- sonic classes), I find it extremely difficult to say which type of cruise missiles
are fitted in the later generations of Akula's. I did not found solid data.
However, it seems likely that one of the "Kalibr" types will be installed in recent Akula's.
Hunter/Killer ordonnance:
For "local" use, to Hunt/Kill enemy vessels or subs, a number of SS-N-15 or SS-N-16 "anti-ship/anti-sub" torpedo's
are available which may carry a 20 kT nuclear warhead.
⇒ The Yasen classes of Submarines (Project 885 and Project 885M):
Note: the "Yasen" class is sometimes also referred to as the "Graney" class.This class, is a new Sub, and is often portraid as the successor of the Akula class.
Thus, the Yasen is primarily an "attack submarine" too, just like the Akula's are.
Ofcourse, the Yasen class subs, use nuclear propulsion.
Many of the Akula's II and III subclasses are still fairly recent, so it will take
a substantial period as from now, before the Akula's are phased out.
Indeed, a few of the earlier Akula's were overhauled, and the last Akula was handed over to
the Russian Navy as recent as 2009.
To be more concrete: the new Yasen subs will live quite some time alongside a number of the
Akula II and III classes.
Ofcourse, as time goes on, the Akula's will go, and their duties will be taken over by the Yasen subs.
In December 2013 the first Yasen, the "Severodvinsk", was ready to enter service in the Russian Navy.
Most reports say that 6 more are in various stages of construction, and it is expected that most of them
will be finished construction, and have went through all sea trials, somewhere around 2023.
One of them (the "Kazan") is now actually under sea trials, meaning that in 2018/2019, two of them
ill be fully operational.
It's quite likely, that 8 will be the total number of Yasen subs. However, this is somewhat uncertain too.
The statements above, only are trustworthy if the Defense budgets of the Russian Federation will not
collapse below certain tresholds. Indeed, new subs like the Borei class are under construction too, and many
developments occur in many other disciplines in the armed forces of the Russian Federation.
Let's compare the dimensions/specs of the Akula's (III), with the Yasen:
Akula III: length: about 113 m, max width: 13.5 m, max speed is largely unknown,
but it is certainly above 32 knots, crew: around 70, Submerged Displacement: around 13800 tons.
Yasen: length: about 119 m, max width: 12 m, max speed is largely unknown,
but again, it is certainly above 32 knots, crew: probably around 70,
Submerged Displacement: around 13800 tons.
Remarks:
- The tonnages listed are no typo's. In most reports, both the Akula III and Yasen "Severodvinsk",
are reported to have a Submerged Displacement of around 13800 tons.
Some other reports list a Submerged Displacement of around 11800 - 12000 tons for the "Severodvinsk". - The number of crew members listed for the Yasen ranges from 50 up to 90 in various reports.
- The Yasen class has an extremely sensitive spherical sonar installed, filling up the larger part
of the bow. - New alloys have been applied with superlow magnetic resolving properties to evade advanced
enemy detecting sensor systems.
Most reports speak of a max depth of around 550-600 m.
There are actually two subclasses of the Yasen: Yasen - Project 885, and the Yasen-M - Project 885M.
As the Yasen subs go through various building/implementation phases, it's quite possible that
newer subclasses will be introduced, each more innovative compared to the former ones.
Main weaponsystems:
Two main types of systems are implemented:
Torpedo's/Missiles for local Hunting/Killing.
Various systems are implemented for hunting/killing of enemy vessels and subs in the (relatively)
local neighborhood. Among that armament are 8 torpedo launchers, implemented as 6x650mm and 2x533mm systems.
Cruise missiles:
The Yasen will be equipped with medium range cruise missiles of various types (3000-5000km),
able to carry a conventional or nuclear warhead.
The last 10 to 20 years (or so), the Russian Defense industries went through a very strong upgrade
in advanced technologies, which is clearly visible in their current types of cruise missiles.
The Yasen class has 8 VLS reloadble tubesystems, where that system is capable of firing multiple
types of cruise missiles. Likely cruise missiles are:
-Onyx series,
-Kalibr series,
-Kh series,
-and very likely even the Zircon class of missiles.
The number of missiles which the Yasen class may have onboard, depends on the mix of cruisemissiles,
but typical figures which are often reported are something in the range of 32, 40.
The cruise missiles can be fitted with a nuclear warhead.
Another section below, will dive a bit deeper in those new cruise missiles, including the Hypersonic missiles.
⇒ The "Belgorod", or Project 09852 class:
I'am afraid that detailed information is not available in the Public domain.Below you may find some information, but nothing seems to be really confirmed in any way.
All available clues, which came available in early 2019, seem to point that Project 09852
is a "special mission" submarine, for a large array of tasks.
The main tasks seem to be:
- That it is a carrier for the Status-6/Poseidon nuclear torpedo. It might have up to 6
of such unmanned drones. Still, speculations exists on the exact details of Status-6.
But it is reasonable (at this date, July 2019), to assume that it is an autonomous device,
which is quite similar to a submerged ICBM, and is likely to carry a 2 Megaton thermonuclear device. - Some articles suggest that it might carry the Losharik (Project 10831) deep-diving midget submarine,
for special operations. Some analists view this smaller sub as a saboteur submarine,
for destroying enemy networks and otherwise placing charges.
Other articles speak of the Paltus minisubmarine, which unfortunately add to the confusion. - It implements and contributes to the Arctic "Harmony" submarine detection network.
Unmanned autonomous stations are deployed at all relevant locations in the Artic seabed,
utilizing hydro-acoustic equipment in order to detect any enemy submarine. - It carries the "Harpsichord" UAV (Unmanned Autonomous Vehicle) or "Klavesin" UAV's.
The "Belgorod" is often portraied is a modified Oscar II sub. However, the dimensions differ
substantially from the Oscar II.
The main dimensions are: Displacement: about 24000 tons submerged, Length: about 178 meters,
Beam: about 15 meters, crew: probably around 110.
It's an enormous sub, but in terms of tonnes, it's still quite smaller than the Typhoon.
⇒ The Husky classes of Submarines:
It might indeed be so, that well after 2020, the Russian Federation will start to build a newsubmarine, which some analysts refer to as the "Husky" class of submarines.
I will leave out any comment on this submarine, since it's still in a design phase, and any real
substantial, and trustworthy details, are not clear to me, yet.
5.2.5. Overview Cruise Missiles with (optional) nuclear Warhead:
The following cruise missiles are of interrest to us, namely the:- 9M730 Burevestnik,
- P700 Granit series,
- P800 Onyx (Oniks) series,
- 9M72x SSCx. Notably the SSC-7/8 series, or related to Iskander-K.
- 9M729 or SSC8 (SSC-8).
- Brahmos series (India/Russia),
- Kalibr series,
- Kh series (including the Kh-47M2 Kinzhal),
- 9K720 Iskander / Iskander-M / Iskander-K (R-500)
- (*) Zircon series.
Important:
-Along the way, I found that a listing like below, will not have accurate data on the specs,
at all times. The listing is good enough for a good "overall impression", however, it's simply
a fact that uncertainties exists in specs like yield of the warhead, max. range, numbers, etc...
-Many older types are not listed here (like the P500 Bazalt etc..). Also, types which are
solely designed for a conventional warhead, are omitted too.
An exception is the family Zircon missiles.
-(*): Zircon: It's very questionable if the hypersonic Zircon could be equipped with a nuclear warhead.
It's likely that it's capabilities will come from pure Kinetic energy and/or conventional warheads.
It seems especially designed to destroy targets through it's extreme velocity (and possibly a conventional
warhead). However, many articles call it nuclear capable, which I simply question to be correct.
-There exists almost no reliable Public details on the 9M730 Burevestnik.
-I find it very difficult to find trustworthy info on several missiles, like the SSC-8 (9M729).
-If any note or article, suggests a treaty breach for a certain missile, a crosscheck with other sources
is mandatory, otherwise the information must be regarded as useless.
-I will not mention any export model (by the Russian Federation) to other states, of any of the missiles.
I have no clue as to how many folks read this simple note. I suspect it's a real low number.
Independent on how many readers there are..., anyone wants, and expects, trustworthy information.
I don't want to dissapoint you, but as with many new military objects in the Russian Defence,
a number of features are simply estimates, while other features are rather preciese.
However, the estimations generally seems vary quite a bit. But the overview is "sufficient"
to "position" the weapon in the military scene.
For a number of cruise missiles as listed above, I cannot say anything else than the some data
remains a bit "foggy", if one is only able to access Public, and open, information.
This is espcially true for the max. range of such weapon, and the type of optional nuclear warhead.
We are going to discuss all of the missiles above, in a very "light-weight" manner. My personal point
is that the cruise missiles which are able to carry a nuclear warhead, are extremely dangerous.
⇒ Ofcourse, we know of the large array of ICBM's and SLBM's, as we saw them in previous sections.
Those ballistic missiles are extremely dangerous, but they are also "embedded" in rather tight
functional/technical protocols, govering the "state" of the missile.
Since they are here for such a long time by now, the protocols also had time to stabilize into
into a "reasonable" set of ways to control the devices. There was, so to say, more time to settle down
into "reasonable" control.
Note: the term "reasonable" does not mean that I agree with any procedure around missiles.
Personally, they are dangerous at all times. The expression is solely in the context, to compare
the procedures around ICBM's, against the downsized smaller products like cruise missiles.
⇒ I strongly believe that "downsized" smaller producs, like cruise missiles, are governed
by less strickt protocols. Although you cannot call them "tactical" anymore, local command structures
may have a large weight in actually deploying the systems.
⇒ Also, they are more likely to be deployed in a smaller/medium conflict between
NATO and the Russian Federation.
⇒ Some of the missiles listed above, seems to be a violation of the INF treaty.
That's my personal opinion, but needs to be made plausible using other sources as well.
⇒ Hypersonic weapons capable of carrying a nuclear payload or conventional charge, have a
a certain intrinsic design flaw. For example, when an ICBM is launched, matters are clear (so to say).
However, if this cruise missile is launched, the opponent does not know if it carries a conventional,
or nuclear payload. This uncertainty may lead to nasty results.
⇒ Quite offensive too, is the application of nuclear propulsion in the "Burevestnik" missile, as it
in principle makes the weapon range and flight-duration, extremely high.
It's also experimental technology, which makes the whole concept a bit of a gamble. Even test scenarios
in peacetime introduces a large risk, even without a payload, since a nuclear reactor is onboard
the missile.
-What defines a cruise missile?
We should not interpret any definition as "too strickt". Ofcourse there are many types of missiles,and every type has it's own set of characteristics.
What is rather typical of cruise missiles, is that they in general:
- After launch, they sort of "cruise" to their target. This may be at very low altitude, following
the terrain, or it might be at higher altitudes.
As an extreme example, there indeed exist sea-surface skimming rockets, which simply fly meters
above the surface. However, generally, they may cruise at any altitude.
- They are not ballistic. They do not leave the atmosphere. Typical altitudes are tens of meters,
to several kilometers above the surface.
However, some cruise missiles may follow a much higher path like 30km. - They may be equipped with a jet, turbo jet, ramjet, or scramjet engine. (Sc)ramjet will be explained below.
Nowadays, especially Russian modern cruise missiles, use scramjet engines, allowing hypersonic speeds. - They usually have (shorter) wings, contributing to the lift, but the body of modern missiles
may contribute as well in lift. - They may use satellite for positioning and navigating, but "terrain contour mapping facilities",
like e.g. TERCOM, might also be used. - In the not too distant past, the majority of types of cruise missiles, typically had a max range
of a few hundreds of km. Ofcourse, many exception existed to the former statement.
In the last few decades, for several types, we saw an increase in max ranges, even up to 1500 km or so,
ot even quite a bit more. - A cruise missile might be launched from the surface (like from a vessel, or truck), but airborne launches
from a plane are often implemented too.
-Sub-, Super-, and Hyper sonic speeds.
-Subsonic means that the missile has a cruising speed below Mach 1. In some technicalarticles the treshold is defined at 0.8 Mach. As an approximation, we will simply use Mach 1.
-Supersoninc generally means that the missile has a cruising speed well above Mach 1.
Usually, the range of 1.3 Mach up to Mach 3, or up to Mach 5, is used to characterize supersonic speeds.
-Hypersonic generally means that the missile has a cruising speed well above Mach 5.
With Mach 5 or higher, speeds are well above 1 mile per second (mi/s), or even quite a bit faster than 1 mi/s.
At such speeds, a conventional warhead might be omitted (depending on the purpose or target), since
the Kinetic energy alone, might be enough to destroy the target, which may be even as large as a Frigate.
To put it in perspective: ballistic ICBM's may reach speeds like Mach 8 up to Mach 22. However,
even though ICBM's are much faster, the special thing about hypersonic cruise missiles is that they may skim
the surface (even though maybe at 30km, 50km or so), undetected, with a nuclear payload.
By the way, due to physical restrictions, the larger part of the path of a hypersonic missile
using a scramjet, has a minimum- and maximum altitude. In effect: it cannot "fly to low", except
for the last phase of it's mission.
-Hypersonic stealth.
With any Hypersonic device propagating in the atmosphere, then it becomes surrounded by regionsof ionized gas, which strongly affect the interaction of electromagnetic waves to and from the device.
As a consequence, Hypersonic cruise missiles have the advantage of being largely stealthy for radar.
You might remember this effect too from spacecrafts, returning into the atmosphere (like Apollo etc..).
While decending at great speed, there were several minutes of complete radiosilence.
It can be said that the Russian Federation has the techical leading position in developing and producing
the extremely fast hypersonic cruise missiles.
High speeds obviously have great advantages. The enemy have great difficulties to detect, target and
destroy the missile. Hypersonic cruise missiles are generally considered as being unstoppable.
Secondly, just the kinetic energy of the missile might be sufficient to destroy the target.
Now, let's take a look at the current cruise missiles, which are in service at the Russian Federation.
From the listing above, a couple have been around for quite some years now, like the P700 and P800.
Other were developend as recent as in the last decade, or the last few years.
⇒ The Zircon missile:
Russian identifier: 3M22 ZirconNATO identifier: SS-N-33
It's indeed clear that it's a formidable weapon, with outstanding performance for the tasks
it is designed for.
For example, it's a device where a Carrier fleet has no adequate answer for.
Some folks classify the Zircon as a "hype", or "hoax", or fairy tale.
That's nonsense, since there is more than enough proof, that it exists. However, there still
might be some fine-tuning issues around, to solve.
It's indeed completely amazing that such an advanced device was so quickly in operational status,
without the (expected) flood on technical issues, since the first prototype in around 2013.
There were indeed some issues on mounting the device in various launching platforms, on various vessels.
A common idea which comes up when browing through many articles, sites etc.., is that the Zircon will be
a rather standard weapon on many sorts of vessels in the Russian Navy, which are:
overhauled older vessels, newer frigates, cruisers, and even corvettes, and ofcourse the subs wich were
desribed in the former sub chapter. As I see it, a multi purpose Vertical Lauch System (VLS) is
under construction, which allow the device to be ported along many types of vessels.
It's a good example of an effort of the Russian Federation to strive to interoperability and integrated
portable systems.
It's not only a sea launced missile. Modifications exist, to launch it from truck or airplane.
The machine is first launched using a small booster stage with solid-fuel, to accelerate it to well above
Mach 1. Then the booster decouples, and the scramjet starts.
Here are the main specs:
-Range: at least 500km, depending on the choosen trajectory (altitude).
Many analysts speak of a range of 500-640km, up to a max of 1000km, depending on the choosen trajectory.
-Speed: above Mach 5. Many reports speak of Mach 6.
-Upgrade: It's likely that the Zircon can be viewed as an upgrade to e.g. the P700 granit series,
using a standard, portable, VLS platform.
- CEP or accuracy: The accuracy of the impact point is extremely high, and must be expressed in meters.
- Warhead: The Zircon is likely to use it's kinetic energy only (resulting from the speed > Mach 5),
but it can be fitted with a conventional warhead too.
For as far as the information goes which I am able to acces, it's likely that the Zircon can be
classified as a non nuclear hypersonic cruise missile.
I can still be wrong here. But I seriously believe, after study of data and missile dimensions,
it will be a non nuclear missile. What is it doing in this note then? The answer is, that I first
saw it as a missile with an optional nuclear warhead. It seems that I was wrong.
Ofcourse, quite some time ago, small nuclear warheads even fitted in Howitzer grenades, so if
some administration really wants nuclear warheads of a few kT, it is possible!
Just think of the M65 atomic cannon, aka "Atomic Annie", which is just an example of a cannon
using nuclear shells. At some time, there were lots of them. Fortunately, the US and Sovjet Union
stopped with this development around 1991/1992.
I guess I want to say that the 3M22 seems not to be designed for having a nuclear charge.
Ofcourse, with lots of effort, anything is possible.
It is safe to assume that the Zircon will be produced in large numbers, since most
operational Navy vessels will be equipped with a mixture of the Kalibr and Zircon missiles.
⇒ The Kh-47M2 Kinzhal / Dagger:
This time, we will see some details of a series which are capable of carrying a nuclear payload.Especially Western forces have some worries about the Kh-47M2 Kinzhal cruise missile.
Unfortunately, not much details around the Dagger can be found. However, some features are
pretty clear. Indeed, the Dagger is a modified "Iskander" missile, which is a surface launched
nuclear capable missile, with a range in the order of 500km. More details are know of the "Iskander".
The "Kinzhal" is lifted to a high altitude, by e.g. a Mig 31K, or a Tu-22M3 airplane.
It's not a scramjet machine. In that respect, it's more like a missile with traditional propulsion.
But it shares important features with cruise missiles, in the fact that it get launched from a plane,
and "cruises" on a path to the target just like a non ballistic cruise missile would do.
You can argue on the fact whether the term "ballistic" or "non-ballistic" path would apply.
But since the "parent", the "Iskander", is a short range ballistic missile, it seems fit to type
the "Kinzhal" in a similar way. Personally, I think a little different. See my interpretation below.
While it thus operates in the atmosphere (like after being launched from e.g. a Mig 31), it accelerates
to a speed > Mach 10, and at some (?) point, it starts to maneuver around something we might call the
"virtual path" which corresponds to the path which, more or less, a regular ballistic missile would take.
We must interpret that maneuvering as evasive behaviour, in order to evade enemy counter measures.
So, since that "virtual" path looks somewhat similar to a ballistic path, many folks would call it
a ballistic missile. But it shares features with cruise missiles too, and that's why other folks
classify it as a cruise missile. Still others, would type it as "aero-ballistic".
After release from a Mig or Tupolev (or other appropriate airplane), it climbs to a certain
altitude (?), then following, is a sort of, what we might call, a virtual ballistic path.
If regarded as a cruise missile, then the features which really sets it apart, are:
-Longer range of > 2000km.
-Air to Surface missile.
-Evasive maneuvering applied, in order to make precise prediction of it's next positions impossible.
-Conventional or nuclear warhead.
-Speed > Mach 10, which is extremely fast.
-CEP or accuracy: must be expressed in terms of 10-20 meters.
-numbers (current or projected): ?
Some analysts view the "maneuvering capabilities" as an implementation of the Avangard technology,
which is applied with the Sarmat too. I personally think it's a different kind, and I think
that "Avangard warhead gliding technology" is only applied with ICBM warheads.
Because of plasma stealh, high speed, and the evasive maneuvering capabilities, most analysts say
that this device bypasses any NATO ABM or "anti-ballistic missile" defense system.
The "Kh-47M2 Kinzhal" is new. Tests were only as recent as in the start of march, 2018.
I have not found good data on the present- or projected numbers of this missile.
Also, I did not found good data on the magnitude of the optional nuclear warhead.
INF breach? No, not according to the precise rules.
I tell you, that I have to be extra extra careful here. The strange thing is, that e.g. the "Iskander"
is occasionally portraid as an INF breach. First you should know that there are quite of few subtypes
in the Iskander family. Some folks have found reasons to believe that a few subtypes have a larger range
than the lower treshold distance of the INF treaty (basically it specifies a range of 500 - 5500km).
Note that this subsection is about the "Kinzal", and not the "Iskander" family of missiles.
But formally, the "Kinzal" is not a violation of the INF treaty. Read the following line closely:
(prohibitive key rule of the INF treaty)
..
..ground-launched ballistic and cruise missiles with ranges of between 500 and 5,500 kilometers..
..
By the way, sea launched missiles are excluded too from INF.
I tell you again, that I have to be extra extra careful here. In the alinea below, you will find my
personal opinion, and conclusions:
Treaties specify a missile as an ICMB, if it can reach a distance over 5500km. The RS-26 Rubezh
have been tested to reach just over 5800km. Thus, it's an ICBM, according to the INF specifications.
However, it's substantially smaller than other current Russian ICBM's, and it's typical targets are
within a radius of 5500km. If you ask me. this weapon, can rightfully been seen as a rather "smart"
bypass of the INF, since this ground-based system obviously can reach targets within 5500 km.
A bit stronger: it's especially designed for distances below 5500 km.
The RS-26 Rubezh was already described in section 5.2.2 (ICMB section), above.
With the cruise missiles, there might be deviations too, if you would ask me.
If the found data on the 9M730 and SSC-8 is correct, these are pretty much deviations too.
If such information, as presented in the alinea above, has your interest, you should always
cross-check such data with other sources. Most of my note is simply a description of nuclear devices,
but the alinea above is a "sort of an exception", and deals about "treaty breaches", which always needs
to be validated with other sources.
If any note or article, suggests a treaty breach, a crosscheck with other sources is mandatory,
otherwise the information must be regarded as useless.
⇒ The 9K720 Iskander / Iskander M / Iskander K / Iskander "family":
Important:I have difficulties in finding consistent data on the various types of missiles.
Some reports seem to contradict, and the specs are quite often not clear (to me).
The Iskander missile forms a rather wide family of missiles.
It started out with a sort of missile, which we really must classify as "ballistic".
Some later types, might be viewed as "cruise" missiles.
Again in short: a main feature of a ballistic missile is, that it follows a path like a fired shell
would do. It's fired from the surface, climbs towards some maximum altitude, then descends towards
it's target. A main feature of a cruise missile is, that it cruises along the terrain, or at a certain altitude,
towards it's target.
-Main features Original 9K720 Iskander (SS-26 Stone or SS-X-26):
-Can be seen as a short-range Ballistic missile.
-Fired from road mobile system (heavy truck).
-Probably replaces the SS-23 spider (launced from truck as well).
-Introduced in 1996, more widely adopted as of 2006.
-Max range is probably around 400km.
-Nuclear or conventional warhead.
-Output of nuclear warhead: could not find consistent data.
-Number of missiles: sometimes reported to be around 112.
-CEP/accuracy: to be expressed in meters.
-Main features Iskander-M:
Often to be reported as a modified (regular) Iskander (see above), but with this instance, strong evasion
maneuvering capabilities have been implemented. The missile performs it's maneuvering
around a virtual ballistic path.
It's sometimes reported to have a slightly enlarged maximum range, of, in the order of 500km.
-Main features Iskander-K:
The Iskander-K might be seen as a "carrier missile" for the R500 cruise missile, or other variants.
Most reports mention that the Iskander-K is a mobile platform for:
-9M728 or SSC-7 or R-500 cruise missile.
This missile is a non-ballistic missile, and acts like a cruise missile.
The reported range is often > 500km.
The missile is nuclear capable. I have not found data on the output of nuclear warhead in kT.
-9M729 or SSC-8 or Kalibr variant.
This missile is a non-ballistic missile, and acts like a cruise missile.
The range is often reported to be > 1500km. (seems to be non-verfified data).
The missile is nuclear capable. I have not found data on the output of nuclear warhead in kT.
As you see, vital data seems to be missing.
But in a subsection below, I will focus on the SSC-7/8 types, and still try to say something useful
on these devices. That's however not guaranteed.
If the "surface-to-surface" missile 9M729 or SSC-8, indeed exceeds the 500km lower INF limit, it can be
interpreted to be in violation of the INF treaty.
Again, if any note or article, suggests a treaty breach, a crosscheck with other sources is mandatory,
otherwise the information must be regarded as useless.
⇒ P700/P800:
Russian Identifier: P-800 OniksNATO Designator: SS-N-26 Strobile.
Russian Identifier: P-700 Granit
NATO Designator: SS-N-19 Shipwreck.
The P-700 seems more involved in Naval activities, like as a surface-to-surface missile lauched
from sub or vessel.
The newer P-800 seems more involved in landbased activities, like as a surface-to-surface missile lauched
from truck or other launching facility, but can be used in Naval activities as well.
From that latter statement, and the fact that the P800 is more recent, it's rather plausible that
the more versitile and lighter P800, is a followup of the P700.
Both missiles are cruise missiles, with a max. speed about Mach 2.5 at higher altitudes.
At lower altitutes, the range and max speed is considerably lower.
The P800 uses a ramjet, while the (older) P700 uses a turbojet engine.
P700: length: about 10m, weight: about 7000kg (fully loaded).
P800: lenght: about 8.6m, weight: about 3000kg (fully loaded).
⇒ The P-800 Oniks / SS-N-26 Strobile:
Note: The name "Yakhont" is often used for the export model.
The P-800 still is a relatively new cruise missile. It became operational in the early 2000's.
It's most likely targets any surface based target, like landbased objects as well as vessels.
The reported ranges vary from about 120km, to 300km, to about 600km.
It's a nuclear capable cruise missile. Regrettably, I have not spotted consistent values
in the yield of the nuclear warhead, in any publication. The max value seen is 500 kT.
Actual published values are very rare, and thus seems not fully reliable.
It seems rather plausible, that this sort of missile can minimally transport a 150kT nuclear warhead.
About the max ranges:
The missile can operate as a surface skimming missile. As such, it's max speed, and max range
is considerably lower, compared to a high altitude cruising route.
This then corresponds to the values of 120km and 300km. It's only that certain reports mention
a max range of about 600km, that I mention that value. It's not known how reliable that latter max range is.
The missile has a ramjet engine, but uses a booster stage brings it up to speed. In this sense, it's
a two-stage missile. It's a hypersonic missile with a max speed of about Mach 2.5.
There exists confirmed footage (photo's) where the P-800 was test launched from Navy vessels,
but from trucks too.
It looks as if the Indian/Russian "Brahmos missile" was based on the specs of the P-800.
Also in appearance, the Brahmos and P-800 look strikingly similar.
The CEP or accuracy, must be expressed in meters.
There are thus uncertainties about a good estimate of the number in operation, and a reliable
value of the yield of the (optional) nuclear warhead.
⇒ The P-700 Granit / SS-N-19 Shipwreck:
It very likely that the P-700 is a candidate to be phased out. It became operational around 1985.
Indeed, a even followup like the P-800 is much more recent.
Since the P-700 seems to be especially equipped for Naval activities, it seems likely that
the Zircon and Kalibr missiles are the moderized replacements.
It looks like this is indeed taking place at various vessels in the Russian Navy.
The P700 uses a turbojet engine, while modern cruise missiles use a ramjet or scramjet engine.
It can be equipped with a nuclear warhead. The largest yield reported is 500kT.
Again, I am not sure about such number, since consistent values are rare. But there can be no doubt
that both can easily transport a 150kT warhead.
Once it was a "popular" cruise missile on various vessels. It's not gone by now, but I guess
that it will be replaced by Kalibr/Zircon's, so the current number of operational missiles seems
to be somewhat less relevant.
⇒ Kalibr family:
It's possible that in this section some names/types are incorrectly used.I am still working at it. It really seems to be a bit of swamp to find correct names
with the correlated types. Sorry for this.
The complexity in the variants of Russian cruise missiles, never stops to amaze me.
What many call the "Kalibr" missile, is not very far from relatives as certain "Kh series".
Also, according to some documents, there exist P900 devices which are also very close in resemblence
to the "Kalibr" too, if I understand it all correctly.
Concepts and some early models even existed as early as the mid-'80's, but the Kalibr only matured
as of (around) 2002.
All the subtypes, have differences in: (1) range, (2) type of launching platform (e.g. Sub, Vessel),
(3) meant for export, (4) nuclear capability Y/N, (5) types of target,
(6) type of possible trajectories (e.g. skimming surface, or higher altitudes etc..),
(7) and if it has the feature of "terminal phase speed boosting capability".
Although there are quite a lot of "relatives", three main types (I believe) can be distinguished,
which most folks would indeed name as the "Kalibr" (Caliber) cruise missile.
It seems to me, that NATO designators like SS-N-30A, or SS-N-27 Sissler, were also in use for some older types
of Kalibr missiles, which typically all had a shorter range like in the order of 300km.
Also, as I found it in various articles, such designators were also applied for "E", or KLUB (Club) export models.
But, to my surprise, the NATO designator like SS-N-30A is (also) (reused?) for a modern longer range model,
like the 3M14.
I must say that I still have not solved this issue in a proper way.
-3M51 / P900 (shorter range missile):
Seems to be a shorter range missile, for about 200-450km. It's about 8m length, warhead about 300kg,
it's nuclear capable, and is especially designed to be an anti-vessel device.
It seems to be an alternative followup for the P700, or P800.
It uses a Turbojet engine. Subversions exist for use on modern (or modernized) Subs, or Navy vessels.
Data is, withouth any doubt, a bit "foggy" to say the least. The data from the scarce documents seem to
point to a device which is a subsonic surface skimmer, with terminal phase speed boosting capabilities,
reaching supersonic speed in that last phase.
-3M14x with NATO designator SS-N-30A (longer range Kalibr missile):
The "x" is a letter which further characterizes the subtype (like "T" or "K" or other). Since articles are
not consistent, I will use the "x" instead.
This is indeed somewhat strange, but the inconsistencies really seem to exist. That is, in my observations.
Here I mean the missile which the Russian Navy used, in firing from the Caspian Sea, to several targets
in Syria, covering at least distances of 1400km.
It's believed that the missile can indeed be equipped with a nuclear warhead as well.
Nowadays, analysts assume (or have reasons to believe) that the max range is somewhere in 1500km - 2500km.
This is the rather well known Kalibr cruise missile. If folks casually talk about the "Kalibr", they often
seem to refer to this particular missile.
It was indeed a sort of surprise to the rest of the World, that the Russian Navy used a Tomahawk-like missile
with even better specs compared to the US/UK Tomahawk.
It also seems that the 3M14(x) is sometimes also referred to as the Caliber-NK complex in some articles.
-3M54 with NATO designator SS-N-27 (longer range Kalibr missile):
I am still not sure whether this only refers to Klub/Club export versions.
Sometimes it is also named as 3M54 alpha, which seems (I am not sure) to be a P900 variant.
Still working on it...
⇒ SSC8 / 9M729 (among other delivery systems, using the Iskander-K):
By now, I have learned that categorizing the various cruise missile systems, really is a daunting task.Since the SSC8 / 9M729 (SSC-8) seems to be a bit politically loaded as well, I must admit that I am scared
not to have the specs in good shape. This is why a pospone this one, until I have better information.
I am not sure at all, but it seems (to me) that some sites/articles just refer to others, in a circular fashion.
As said, I am not fully sure here.
Ofcourse, I have a completely insignificant website. Indeed. Who reads this anyway?
Nevertheless, I fully admit, I am scared to use wrong information.
⇒ 9M730 Burevestnik:
The information in this subsection is unfortunately quite minimal too.For a large part, it expresses my personal observations/opinion.
Missile: 9M730 Burevestnik
NATO designator: SSC-X-9 Skyfall
Personally, I believe it's a reality, however not in a production state.
Some credible articles mention test flights, where an unknown number have simply failed.
When one steps into information on this device, it looks like you are reading the script of some
James Bond movie, or reading some Marvel comic.
It sure is not easy to believe any sort of intel on the Burevestnik.
The key point namely, is the application of a nuclear-powered ramjet engine for use in the Burevestnik.
When we say "nuclear powered", we do not talk about the warhead. No, here we mean the application of
nuclear power in the propulsion system, leading to an virtually unlimited range of the missile.
Many folks doubt it's existence, or are very skeptical. Others say that it is pure bluf.
You may wonder why I still am diving into this one, while there exists so much uncertainties around
this special type of cruise missile.
I think that, so to say, premature concepts of both the "Kanyon/Poseidon", and the Burevestnik, were "born"
when the cold war was at it highest. Not with those specific names, or with any technical detail available.
No, just as concepts. However, slowly, and especially after 2002/2003, the ideas got more and more momentum.
Just think of it: It's far more easier to stuff a large (autonomous) long range torpedo with a high-end
nuclear device, compared to an enormous expensive "Star Wars (SDI)" project, as the US once was planning
to implement. Such a large torpedo (sort of unmanned sub) then should be something like the equivalent
of an ICBM, making the SDI project much less efficient. Especially if you have a large number of such devices.
So yes...: The ideas were born long time ago.
Do not forget, the US already tried a similar project (of a nuclear powered missile), in the early '60's.
This was the "Pluto ptoject", and the US even got quite far with that, until the futher costs and revenues were
again evaluated, the project was halted. Also, US ICBM technology strongly improved at those times, which was
additional motivation not to persue this project further.
Both the paperbased "Kanyon/Poseidon", and the "Burevestnik" concepts, got even more life-elixer,
at the time where the US announced it Star-wars (SDI) project. As we know, the Star-wars (SDI) project never
really came from the ground.
Shortly after, the USSR collapsed, due to various reasons.
The later "Russian Federation", rebuilded itself. In later phases, Pres. Putin did played an important
role is East-west relations. I think we can say that (more or less) as of 2002/2003, the relations seriously
started to deteriorate.
In June 2002, the US withdrew from the "Anti-Ballistic Missile Treaty", and plans were deviced to place
ABM systems in Poland, Czech republic and other states.
It must be said that the Russian Federation itself, dropped the START II treaty, shortly after the US
dropped the ABM treaty.
At that point, the older projects "Kanyon/Poseidon", and the "Burevestnik", were revived, and actual
research started.
As the Russians often have declared themselves, new ABM systems in Eastern Europe, threatened the
strategic balance between the US and the Russian Federation, and that they would come with
appropiate countermeasures.
This is not my theory: With respect to these older ideas of the superweapons, there exists quite a few
articles studying the arms race, as of 1945, from a historical/sociological perspective.
This sort of information, combined with the speech of Pres. Putin, when he addressed his nation at
march 1, 2018, and specifically mentioned this special type of cruise missile, makes the existence
of the Burevestnik very likely.
In the Public domain, there is hardly any solid information on the Burevestnik, with respect of dimensions,
details of the engine, type of warhead etc.. etc..
I don't think that you must doubt it's existence. Although I also believe it's not in any form of
a ready production state.
Finally, I find it an offensive weapon, and even dangerous in peace time, including test flights,
even without a warhead, since the device carries a high-energy nuclear reactor.
The autonomous nuclear armed torpedo, that is, Status6/Kanyon/Poseidon, was covered in section 5.2.4.
Concluding remark about all of the cruise missiles listed and described above:
I started out this section (5.2.5), with an impressive list of modern cruise missiles.
But..., I must now admit that there are truly lots of missing pieces in the specs of those machines.
I am sorry for that, but this is simply what it is....
5.2.6. Supplies of fissile materials and imports/exports:
I was planning to do this for the Russian Federation only. Presently, I think I will shift gear a bit.I will do a more ambitious project: namely supplies of fissile materials and imports/exports
for all nuclear capable countries.
This will be the main subject of Chapter 6. So, anything meant for this subsection, will be in
Chapter 6.
Sofar about The Russian Federation. New information, or updates, will be placed in this section.
5.3 Main current nuclear weapons of France.
5.3.1. Current overview main nuclear systems:
In februari 1960, France performed their first test of a fission bomb.Thereby it became the fourth nuclear capable state (after the US, Sovjet Union, and Great Britain).
It seems reasonable to assume that currently, France has about 350 nuclear devices "Operational/Stockpiled".
-The majority is meant for use in SLBM's on submarines.
These can be considered to be strategic weapons.
-The best estimation I could find is a figure of about at least 50 reserved for Air-Surface missiles,
most notably to be mounted on the Rafale, and still too, for some Mirage types of airplanes.
These can be considered to be tactical weapons.
-Unknown how many are "somewhere" in the chain of development, up to Candidate for dismantling.
The French government, on several occasions, declared that a number of 300 devices would fit
their policy of deterrence.
At a glance:
| Tactical weapon systems: | |
| ASMP, and ASMP-A cruise missiles: | Range: about 500 - 600 km. Speed: about max Mach 3. Warhead: probably 150 kT - 300 kT Specifics: ability to cruise at low altitude. Delivery: fired from Rafale. Number: around 50 |
| Strategic weapon systems: | |
| Triomphant class of nuclear submarines |
Number of subs: 4. Fitted with SLBM's: each sub with 16 SLBM's. SLBM: M51 or M51.2 (French design, and development). Range: probably max 8000 to 10000 km. Speed: probably max Mach 20 - Mach 25. Warheads: likely to be 6 in MIRV configuration, per missile. Warhead probably 100 kT. For the M51.2: 150 kT. Accuracy (CEP): probably around 200m. |
5.3.2. Tactical nuclear weapons:
History:France had quite an array of free-fall (gravity) bombs, succesively in operation during the '70's
up to the early '90's, like the AN11, AN22, AN52 and several others.
These were operated by fighter jets, like certain (adapted) Mirages, or adapted bomber planes.
Since the early '90's. They have all been decommissioned.
Currently:
Most notably the ASMP, and ASMP-A cruise missiles, fired from Rafale, Mirage, and comparable planes.
Highly likely to be distributed among the Airforce and Air-Naval services (Navy).
ASMP-A:
Range: about 500 - 600 km.
Speed: about max Mach 3.
Warhead: thermonuclear warhead, probably 150 kT - 300 kT
Specifics: ability to cruise at low altitude.
Delivery: fired from Rafale, and some Mirage types.
Other modern cruise missiles, like the "Perseus", are not candidates for nuclear warheads.
5.3.3. Strategic nuclear weapons:
Most notably the new Triomphant class of nuclear submarines, equipped with SLBM's (16).Four of those vessels are in operation, as of 2010, with no plans for others.
SLBM: M51 (or M51.2:), French design, and development:
Range: probably max 8000-10000 km.
Speed: probably max Mach 15 - Mach 25.
Warheads: likely to be 6 in MIRV configuration, per missile.
Thermonuclear warhead, probably 100 kT. For the M51.2: 150 kT.
CEP: probably around 200m.
It's not clear in howfar older types (SLBM M45) are preserved or dismantled.
The new ASN4G cruise missile (in development?):
It seems that France started developing the "ASN4G" cruise missile, most often seen by
various analysts, as to be France's first hypersonic cruise missile.
One of the other requirements seems to be, that the device must have a max. range of at least 1000 km.
It can be viewed as the successor of the ASMP-A, and it will likely use a nuclear warhead with
a yield of 150 kT - 300 kT.
There are still uncertainties around the ASN4G. Various articles mention two main routes which
development might take:
-The Camosis type, which is highly tuned for stealth and with a max speed of 4,000-5,000 km per hour.
Then this would be a supersonic device. The minimum max range (1000 km) would apply here.
-The Prometheus type, which would become a true hypersonic missile (> Mach 5).
The minimum max range (1000 km) would apply here too.
Sofar about France. New information, or updates, will be placed in this section.
5.4 Main current nuclear weapons of Great Britain (UK).
It must be understood that here, we only talk about nuclear capable devices.That is, SPEAR, Brimstone, Harpoon missiles etc.. etc.., are not of immediate interest here.
5.4.1. Current overview main nuclear systems:
-The British Government does not have an open policy on it's own nuclear arsenal, in terms ofnumbers, and sizes of nuclear devices.
An often heard number (in magazines, wiki's etc..) is "about 200" devices, of which we may assume
that they are reserved for the Trident II D-5 missiles in the Vanguard-class submarines.
-Also, the British Government, in principle, still allows US nuclear weapons to be stored on British soil.
Formally, the nuclear deterrence is solely build on 4 modern SLBM based Vanguard-class submarines.
Those entered service in the period 1993 - 1999.
A programme for the successor of the Vanguard class is accepted.
In 2016 the Britsh decided to start to build a fleet of 4 new "Dreadnought-class" submarines,
likely to be operational somewhere around 2028 - 2030.
Presently, there seems to be a lack of nuclear tactical capabilities. But the strategic component
is very strong, based on the 4 SLBM based Vanguard-class submarines.
However, it's possible that Vanguard-class submarines may carry (when needed), medium range missiles,
or other better optimized delivery systems for shorter ranges, instead of Tridents.
It's simply not disclosed information. It's dangerous here, to slip into speculations.
Notes:
(1): A popular US tactical weapon is the nuclear B61 gravity bomb (thus dropped from airplane).
There exists a number of subversions of such weapon. It's not impossible that such bombs
are stored in the UK as well, as they are indeed stored as well in some NATO countries.
(2): In present day climate between East/West, in my opinion, it cannot be excluded that the UK
might consider introducing nuclear capable cruise missiles. That might be seen as a strange remark,
but the UK seem to value independence more than most other W. European countries.
Ofcourse, this is shamelesly speculative.
At a glance:
| Tactical weapon systems: | Officially: none. |
| Strategic weapon systems: | |
| Vanguard-class of nuclear submarines |
Number of subs: 4. Fitted with SLBM's: each sub with 16 SLBM's. SLBM: Trident II D-5 missiles (US development). warheads: up to 6 or 8 in MIRV configuration. Standard as 100 kT. Selectable between various kT output. Range: US Trident II D-5 about 12000 km. Max speed: around Mach 15 - Mach 24. Accuracy (CEP): probably around 200m. Missiles exist in a "shared pool" with the US. Number of British reserved missiles: likely around 200. |
5.4.2. Tactical nuclear weapons:
Formally, it seems to be none. And formally, it is declared to be none.This used to be very different in the past. For example, around the end of the '80s, the UK had around
250 tactical weapons, of which most of them were WE-177 bombs that could be dropped from e.g. Tornado jets.
A smaller number of other types of bombs (most designed to be delivered by plane), were around too.
It's said that all of them were decommisioned.
It's possible that Vanguard-class submarines may also carry better optimized delivery systems for shorter ranges,
instead of using Trident SLBM's.
Also, it's possible that still Tridents can be given a "sub-strategic", or "near-tactical role",
if the British wishes to do so. For me personally, it's a bit hard to see how a MIRV based
long-range missile, can be put in a tactical short-range role. I can be very wrong here.
Furher, I could speculate about many alternatives, but it's not allowed to do so.
However, it's no secret that the smaller B61 tactical (gravity) bomb, is also stored at some other NATO member countries.
The effectivity of B69, is seriously doubted by many experts, since in Europe, the East side (Russia) is extremely
well defended. Likely, no "non-stealth" jet, or bomber, will get through.
Still the US keeps on developing the B69 further. The "12" version will be better, and true stealth jets/bombers
may be seen to be very effective. Personally I think different, and stealth jets/bombers was a nice idea in the
early 2000's, but no more with modern multi-radarfrequencies SAM batteries.
5.4.3. Strategic nuclear weapons:
Excusively by the Trident II (D-5) missiles in the 4 Vanguard-class submarines.Per submarine:
Tubes: 16 launchtubes. 16 Trident missiles. It's reported that generally a "partial fill" is in place (likely 8).
warheads: up to 8 in MIRV configuration. Thermonuclear. Standard as 100 kT. Selectable between various kT output.
Range: US Trident II D-5 about 12000 km.
Max speed: around Mach 15 - Mach 24.
Pool: The Royal Navy shares their missiles from a shared pool with the U.S. Navy.
Sofar about the UK. New information, or updates, will be placed in this section.
5.5 Main current nuclear weapons of India and Pakistan.
After studying the region near their border, from different perspectives, I would call it "quite hot"for a possible military nuclear confrontation, in a near future. This is suspected among a few people,
but attention in the public, or media is rather low, as it seems to me.
India is arming itself to the teeth. Pakistan is under a high pressure due to the explosive growth of the
population, low economy, and the increasing lack of vital resources, like water.
The latter rescource is quite a complicated factor in border regions. For example, construction of dams,
might hugely impact the population on one side, in large areas near the border.
I am not sure how many folks will take a look this note: I think that the numbers are very low.
But for the few souls that do: I can recommend you to take a look at the geo/socio/political factors
around resources claimed by India and Pakistan, which can directly impact the lives of many millions of people,
like water.
This combined with the fact of territory disputes, and nummerous armed conflicts since 1947,
makes the idea of a larger war, a real possibility.
For a good evaluation, a deep knowledge of geo/political/social structures in that regions is
very important too.
Depending on it's location, the Pakistani's missile "Shaheen III", is practically able to hit
a state as Israel, and surroundings, as well. How is that being evaluated by relevant Organizations?
Well, you may say that the same holds for almost all other nuclear capable States like
the Russion Federation, India, China etc..
It seems that I am sort of speculating, or hinting, on the degree of stability of States.
Indeed, I personally do not think that Pakistan looks pretty "stable", like in politics, and
social environments.
So, let's try to investigate the current status of nuclear weapons in both countries.
Important:
-It's simply a fact that large uncertainties exists in specs like yield of the warheads, max. range, numbers of
deployed devices, numbers in development, etc...
This is simply due to the fact that reports deviate, analysts have different opinions etc..
The listing is however good enough for a good "overall impression".
-Both countries do not provide clarity of their nuclear forces.
While India has quite a deep military relations with the Russian Federation, a similar relation
exists with Pakistan and China.
All those socio/political relations are ofcourse rather complex, and enormously interesting.
But, that's not the subject of this note.
It's a completely different sort of science, if you want to study such subject, into a reasonable,
and accurate, level, it has to be Academic. For a decent analysis, this is mandatory.
In that respect, this text is a very primitive sort of note. It's merely an attempt to "list" devices
and features of those devices.
Commonly, many sources often attribute 130 to 160 operational nuclear devices, to each country.
For me, it's more like 150 to 180 operational nuclear devices, if indeed a relevant portion of the sum
of operational missiles (and also SLBL's for India) can be equipped with nuclear weapons.
However, for both countries it's also true that the facilities to aquire weapon-grade U and Pu, is
rather large, and has increased as of about 2010, due to an increase in nuclear facilities (nuclear plants).
In two subsections, I like to discuss Pakistan and India seperately. It could be true that some capabilities
are overstated, like MIRV capabilities. MIRV capability is "true" ofcourse, but possibly in a somewhat
primitive implementation. Don't get me wrong: I certainly take their nuclear arsenal very seriously.
Indeed: Both countries take each other very serious, for about the conventional- and nuclear arsenal.
The following is just an example: Recently India signed a deal with the Russian Federation
to purchase S400 SAM systems. These can indeed also be seen as ABM systems.
I will review the ABM systems on both sides too, ofcourse.
5.5.1. Pakistan:
⇒ Nuclear capable MRBM's, SRBM's, cruise missiles from Pakistan:
The first two missiles in the table below, are very recent and might only be called operational,in the sense that Pakistan have build at least a few of them which are able to be launched.
The Shaheen missiles cleary carry a Chinese footprint, as is claimed by many analysts.
Often, it is claimed that the Ghauri missiles are similar to the NK Hwasong-7 or NoDong 1 missile.
Those claims can be found in serious literature and articles, and are consistent.
I find it very disturbing in how recent the most modern missiles are (ballistic- and cruise missiles).
It looks like that the arms race between the two States is accelerating.
The table below, is far from finished.
Table: Nuclear capable missiles of Pakistan. There might be a few that I have missed.
This Table is Valid for 2018/2019.
| Name: | Type: | Range: | MIRV capable: | Currently operational: | Number: | Nuclear payload(s): |
| Ababeel | MRBM | around 2200km | Likely | Yes | ? (low) | Yes |
| Shaheen III | MRBM | around 2700km | No | Yes | ? (low) | Yes |
| Shaheen II | MRBM | around 2000km | No | Yes | likely well over 10 devices | Yes |
| Ghauri II | MRBM | around 2000km | No | Yes | likely well over 20 devices | Yes |
| Ghauri I | MRBM | around 1500km | No | Yes | likely well over 20 devices | Yes |
| Babur I | Surface launched Cruise missile | max range 700km | Yes | likely well over 10 devices | Yes | |
| Babur II | Surface launched Cruise missile | max range 750km | Yes | likely well over 10 devices | Yes | |
| Babur III | Submarine launched Cruise missile | max range 500km | Yes | likely well over 10 devices | Yes | |
| Ra'ad | Air launched Cruise missile | max range 350km | Yes | ? | Yes | |
| Ra'ad Mark II | Air launched Cruise missile | max range 550km | Yes | ? | Yes | |
| Ghaznavi | SRBM | around 300km | No | Yes | likely well over 20 devices | Yes |
| Nasr | SRBM | around 90km | No | Yes | likely well over 20 devices | ? Likely not |
All missiles above can be equipped with a conventional, or nuclear warhead. Except for the Nasr,
of which I am not sure that it can use a Pakistani manufactured nuclear warhead.
As you can see, I largely did not even succeeded to find trustworthy numbers of devices.
By now, I am quite sure that reasonable estimates of the numbers of such missiles are
impossible to produce (unless maybe, one is able to access classified information).
As of the Shaheen MRBL's, a certain level of evasive maneuvering capabilities, seem to have
been implemented, according to various sources. For the Ababeel, that is MIRV with evasive maneuvering
capabilities, is no less than enormous technical achievements.
The table above is not quite ready yet. I am still checking in how far the other cruise missiles
are operational. There seem to be a few additional ones indeed.
⇒ Nuclear gravity bombs Pakistan:
Both countries are large. India is even enormous. Both are very powerful from a militairy pointof view, nuclear and conventional. In both countries, the terrain is really tough.
But both will not "win" a nuclear war. In such case, there will only be losers, including
the rest of the World.... Including You and Me, no matter where You live...
Conventionally, Pakistan will not win from India, simply because of the hardware and manpower
at disposal of India.
India: became a nuclear State in May 1974.
Pakistan: became a nuclear State in May 1998.
Before missile technology really matured, since the early 2000's, both Nations relied much on
delivery of gravity based nuclear devices, in other words, simply free-fall "bombs", using Jets and Bombers.
Ofcourse the Ra'ad seems to be a preferrable device for a tactical delivery, as well as the short
range ballistic missiles (for tactical delivery).
The airforce is impressive indeed. Close to a 100 F16's, a large number of Mirages, and a large
number of (largely) Chinese build JF-17 Thunder. The JF-17 is inspired by a mix of several planes
and a predecessor might be the J-7 / Super 7, ultimately ending in the JF-17.
It cannot be denied that it "looks" like a hybrid of the F16/Mig21.
Most articles however state, that the JF-17 is jointly build by China and Pakistan.
Also, most articles speak of a very capable, and affordable multi-role fighter/bomber.
Apart from those planes, a dazzling array of other fighters, bombers and supporting planes
form the Airforce of Pakistan.
Ofcourse, the central question is: which planes can carry nuclear gravity bombs, and possibly
the Ra'ad (or comparable) missile?
Again, I have some difficulties here. Some Mirages are certainly capable. But what about the JF-17?
I simply did not found convincing facts, that the JF-17 is a nuclear capable fighter jet.
There exists indeed data which expresses numbers of squadrons/planes, capable to deliver
nuclear gravity bombs. However, there still exists lot's of unclearity, at least for "me".
I have to pospone this for a moment.
⇒ Stability and Security Risks:
The following is not my theory: Some researchers have expressed serious doubts with respectto security protocols around the nuclear arsenal. Nothing is silo based. All those
surface based missiles are supported by "Transporter Erector Launchers" (tel), or in other words,
road mobile launchers. Especially, the smaller SLBM's are very "movable".
One might argue, that the more a device fits a tactical role, the higher such risks are.
Ofcourse, such considerations are in conjunction in how far you would consider Pakistan
to be a stable state, and in how far extremist groups have certain support in the country.
Many professional studies have been performed on Nuclear security, on India and Pakistan.
In general, the image that emerge, is that India seems fairly aware of all possible security
issues on all Nuclear objects (not only weapons systems, but also nuclear plants, storage etc..),
and for Pakistan, there seems to exist a lesser awareness of Nuclear security in general.
It's fine that rather positive reports exist. My own opinion is less positive, and that
primarily focusses on smaller tactical units.
But we also see that Cyber attacks increase, on a Global scale. I have no clue how far
Pakistan and India have taken appropriate measures against e.g. cyberattacks.
Do not listen to me, along a multitude of rather positive reports: I am not positive.
There is a higher risk for Pakistan, certainly for smaller, mobile, tactical units.
Even a dumb skull like me, can imagine that these might be interesting "targets"
for certain dangerous groups.
I wonder if sufficiently "monitoring" is in effect, if at all desirable, on any
nuclear risk, for both Countries.
⇒ Naval forces Pakistan:
Presently, this is a rather large, but not very modern force. First, the coastline is not large, certainly not incomparison with India. Secondly, Pakistan seemed not to be a state which can afford a large new, modern Navy.
However, is the above really true?
To me, the aquisition of 4 new Chinese Type "054As" frigates, came a bit as a surprise.
Also, the likely aquirement of Turkish and Chinese corvettes is not a small investment either.
The airforces and landbased military, are certainly impressive. The Naval forces used to be relatively small,
and outdated. However, quite a collection of new ships have been ordered.
It looks laike that PAK Navy is, or at leat will be, quite a force.
Next to the larger frigates, and corvettes, there are many smaller patrol/missile boats.
However, it's a bit hard to see how many vessel are, and will be, fully operational now, and the coming years.
This statement simply arose due to rather severe budget limitations imposed on the whole of the Pakastani economy.
Four new Chinese Type "054As" frigates: (4053ton/134m/14500km range)
This is about a modern, powerful, multirole Frigate. These entered service in the Chines Navy, around 2007.
Pakistan ordered 4 of such vessels, and it's likely that they will enter service as of 2020 and upwards.
These will mean a large boost to the capabilities of the Pakistan Navy.
Older frigates:
The Zulfiquar-class (4), Tariq-class frigate (4), and one older American frigate.
It's likely that some will be decomissioned, as the new "054As" frigates will enter service.
Submarines:
PAK Navy operates 5 older subs, and likely some Chines Yuan-class submarines too, in the near future.
Question is, how "operational" these subs really are, since low economics might hamper those subs too.
Anyway, the members are 3x Agosta 90B class subs, and 2x Agosta 70 class subs.
Finaly we enter the "nuclear part" of this section, since the Agosta 90B class subs are SSC subs,
meaning that submarine launched cruise missiles are their primary armament.
Various articles have made it plausible that these vessels are fitted for the Barbur III cruise missile,
which can carry a nuclear payload.
5.5.2. India:
Next, we are going to discuss the nuclear capabilities of the 4th Military Poweron this Planet, namely India.
The military forces are indeed large, and is increasingly modern and sophisticated.
Let's look at a few examples:
(1). For example, the "INS Arihant" (Arihant class) is India's first Nuclear-Powered Ballistic Missile submarine,
equipped with K4 SLBM's. It's the first fully operational vessel, out of a projected number of 4 of such
vessels in total (some articles even speak of 6 vessels). The category of vessels is called the Arihant class.
The second sub, the "INS Arighat" is close to completion, and might begin seatrials somewhere in 2020.
(2). Recently, even a modern (Indian build) Aircraft carrier began seatrials. This is the "INS Vikrant".
It might be put in service, and be fully operational, somewhere in 2020.
It's desplacement is around 40000 tons, with a length of 261m.
It has adequate armament, and all needed facailities, as might be expected from a modern Carrier.
But really special is probably the fleet of (around) 26 - 30 "MiG-29K" fighter/bombers,
which the INS Vikrant will host.
The 29K is a specialized (e.g. reinforced) MIG-29, for usage on a Carrier. All analysts agree that
the MIG-29 is an allround and formidable machine.
The INS Vikrant, currently is not the only carrier. India operates the "INS Vikramaditya" too, which
is a rebuild/refitted Kiev class vessel from the Sovjet Union. Another rebuild carrier is the "INS Viraat".
See below.
(3). Missile technology.
Remember e.g. the Chandrayaan-1 mission (2008) to the Moon? No doubt India even masters the technology
of launching, guiding, and entry, probes to the Moon, and even for controlled decends to the Surface.
You might e.g. also take a look at GSLV Mk-III rocket, and comparable, to get an impression of
the capabilities of India's Space Agency (ISRO).
Ofcourse, the above example is for scientific (peaceful) missions. But it gives you an idea too
on India's capabilities and missile technology.
If you want, you can find nummerous examples. Ofcourse, below, I will focus on military missiles only.
5.5.2.1. Current SLBM's and nuclear submarines from India:
(1). Arihant class Nuclear-Powered Ballistic Missile submarines and armament.
The first sub, is equipped with 4 launcing tubes. The 3 later subs, of which the dimensions aresignificantly larger, will be equipped with 8 launching tubes.
As it seems today, two main types of medium range SLBM's form the primary armament.
No specs have been disclosed on these missiles, but various articles estimate the following:
K-4: Likely completed testing. Max Range 3500km, warhead about 2.5 ton. Likely no MIRV yet. CEP: in meters
K-15: Likely completed testing. Max Range 750km, warhead about 1.0 ton. CEP: ?
I have not found any details on the warheads.
The K4 is likely to be the first choice SLBM for this class.
(2). Leased Subs from the Russian Federation.
Just recently, India made a deal with the Russian Federation to lease the third nuclear poweredsubmarine, of the Akula class.
I am not sure if this third one, is meant to replace a former leased sub (INS Chakra).
However, it seems very likely to be a replacement of the INS Chakra (I).
It's not very easy to find out, if, on the longer term, India will operate just one, or two
leased subs from the Russian Federation. But all signs added up, I think it will be one vessel in total.
But it could also handle about two vessels. No source is fully conclusive enough.
So, for the leased Akula class: it's either one or two.
As you might have read from section 5.2.4, there actually are three subclasses in the Akula class,
namely I, II, and III, depending on the "generation" of subtype of vessel, and specification.
In case of India, it seems currently to be about the Akula I class type of vessels.
If the latest "lease" from Russia will be executed, then that sub will be an Akula II sub.
These vessels are not SLBM capable machines, instead, there focus is on hunting/killing.
And indeed, those subs are extremely capable for their tasks.
There is however, optional capabilities of nuclear torpedoes and nuclear capable cruise missiles,
since the Russian counterparts simply have these options.
It seems extremely unlikely, that Russian ordonnance is availble for those leased machines.
Thus, it's very likely that the Indian vessels will use conventional ordonnance only.
It might be so that a main motivation as to why India leased those hunter/killers,
is to counteract any Foreign threats from any of the seas in their vincinity. You must also know,
that especially the relation between India and China, is not very good indeed.
In that perspective, those vessel(s) expose a serious deterrence for anyone approaching the territioral zones
of India.
(3). Other conventionally powered, not nuclear capable, Submarines.
There exists a considerable fleet of conventionally powered, not nuclear enabled, subs.These are models in the Kalvari class, Sindhughosh class, and Shishumar class subs.
In total, we seem to have 12 - 15 vessels here.
It's a rather powerfull conventional force, mainly of attack submarines, armed with variety of
torpedo's, cruise missiles, and several forms of ordonnance against ship- and landbased targets.
For our discussion: this category is likely not nuclear capable, or intended to be.
Conclusion for submarines: only the Arihant class of Nuclear-Powered, SLBM submarines,
are nuclear capable.
5.5.2.2. Nuclear capable ICBM's/MRBM's, and cruise missiles from India:
It was only until the early 2000's, that India solely relied on the use of free-fall/gravity bombs,delivered by e.g. Mirage 2000 fighter/bomber jets (and similar planes).
However, since that time, the development of nuclear capable ballistic missiles, took off
sharply, resulting in quite some array of nuclear capable missiles today.
To get a good idea of India and socio/political relations, the best way is to dive into
Academic studies, since all the rest might be a bit unreliable, or a bit flawed.
You might wonder what that statement above, is doing here. There might be multiple "drives"
that motivates India to build their arsenal, as to what it is today.
- One thing is beyond doubt: India and Pakistan are both in an armsrace, and they are "doing well".
Fortunately, there are indeed a few bilateral treaties in effect, and both parties have
an open "hot line" in case nuclear escalation threatens.
- India/China relations are pretty cold too. There have been some armed collisions (1962)
and some nasty aftermath eversince. You might want to consult historical material on all
of these issue's.
Just imagine, in just over 15 years, an enourmous development took place with respect to
ballistic- and cruise missiles. This justifies to say that India tries to arm itself
to the teeth, and certainly makes no joke about it.
I know myself ofcourse, that the above sounds a bit silly perhaps. But this is my own
observation and interpretation. Yeah, what exactly is going on? Are Pakistan and India
so afraid of each other, or do we mis something?
Or is perhaps the USSR-USA cold war of the '70's/'80's, mirrored here?
Do you generally hear much comments from World Community about it? Personally..., I hear nothing...
For those Indian Nuclear capable ICBM's/MRBM's/SRBM's, and cruise missiles, I collected
the following information:
Table: Nuclear capable missiles of India (except very short range, which are not listed).
This Table is Valid for 2018/2019.
| Name: | Type: | Range: | Nuclear capable: | MIRV capable: | Currently operational: | Number: | Max speed "v": |
| Brahmos I | Cruise missile (landbased) | 300-500km | likely no | - | Yes | Significant number | Supersonic (mach2 < v < mach3) |
| Brahmos II | Cruise missile (landbased) | ? | likely no | - | In development | - | Hypersonic (v > mach5) |
| Airlaunched Brahmos | Cruise missile (airlaunched) | ? | likely yes | - | In development | - | Supersonic (mach2 < v < mach3) |
| Nirbhay | Cruise missile | around 1000km | likely yes, around 10kT | - | close to Production | - | Subsonic. Most test were completed. |
| Surya (undisclosed) (*) | ICBM | 8000-12000km | Yes, MIRV 3-6, each 250kT | Yes, 3-6 | Test phases | Test/Pilot specimens | - |
| Agni 5 | ICBM | 5000-8000km | Yes | Likely, # of warheads:? | Likely still in development | low number | - |
| Agni 4 | MRBM | up to 4000km | Yes, likely 150kT | No | Operational | low number | - |
| Agni 3 | MRBM | up to 5000km | Yes, likely 150kT | No | Operational | Significant numbers (>10) | - |
| Agni 2 | MRBM | up to 3500km | Yes, likely 150kT | No | Operational | Significant numbers (>10) | - |
| Agni 1 | SRBM | up to 1000km | Yes, likely 20kT | No | Operational | Significant numbers (>10) | - |
| Prithvi-I Prithvi-II Prithvi-III Dhanush |
SRBM's | 150-300km, III:700km | Yes, likely up to 20kT | No | Operational | Significant numbers (>20) | Supersonic |
(*) The Surya is still subject of debate. Some analysts even question it's existence.
Indeed, a number of conflicting reports exist.
However, like all Superpowers, a longrange ICBM (>10000km) is a true "added value" to the
deterrence of a Nation, that is, deterrence on a Global scale. This makes the existence of the Surya
(or Agni-6?) more than likely, also given the proven techniques and highly skilled levels
within ISRO and DRDO.
There exists indeed some confusion around the Surya, and the Agni-6. Some analysts maintain
that one development takes place, known under the names Agni-6 and Surya. This means that
both names would then refer to the same project. For me personally, the confusion is not resolved.
-It's not certain if India really masters MIRV technology, but it seems very likely
that it has that capability, again given the proven techniques and highly skilled levels
within ISRO and DRDO.
-As was true with Pakistan, I was not able to produce reliable numbers of operational devices.
-However, for an "impression" of India's capabilities for ICBM/MRBM/SRBM and cruise missiles,
the table above might be of some assistence.
5.5.2.3. The Airforce and free-fall (gravity) bombs:
Possible developments:
-There were some advanced projects started up, like an agreement with the Russian Federationto develop a derivative of the Sukhoi SU-57. The status of such projects at this time,
regrettably is not clear. One thing is quite sure, the Su-57 is very expensive, so a question
might be how far that adventure goes. Indeed, it's very ambitious.
The Su-57, like the US F-22 Raptor, are considered to be the most advanced fighter/bombers today,
in terms like speed, range, agility, stealth, and nuclear carrying capabilities.
Sorry I am not able to say more about it.
-Nirbhay: Although the Nirbhay cruise missile originally is developed to be launced from mobile landbased
platforms, development for a derivative for launch from a fighter/bomber, is utterly likely.
There were indeed some startup problems with the Nirbhay, but today (june 2019), the machine
goes rather "well" I believe.
Various Su models are good candidates for carrying that missile.
There is absolutely no doubt in my mind, that India will pursue that road.
-Airlaunched Brahmos: This cruise missile originally is developed to be launced from mobile landbased
platforms. However, an Airlaunched Brahmos is practically operational, which is likely to be
nuclear capable. Recently, tests were performed using the SU-30MKI fighter/bomber jet.
Current Force fighter/bomber jets:
A large part of the Airforce consists of Jaguar and Mirage 2000 fighters, which needs to be replaced.But things are not very clear. It might also be true that a number of those Jaquars and Mirages, simply
get's upgraded. As a main party, the ways how Hindustan Aeronautics Ltd (HAL) operates over time,
is not always cristal clear.
True replacements are also in progress, and for example, some Rafale fighter/bombers
are already ordered, and a small number might be in service right now.
It's however not possible to give an exact table of operational jet fighter/bombers, since the
process is taking place, and it seems that occasionally, a certain choice has been changed
to an alternative choice of fighter/bomber.
It also looks like that several setbacks and delays have seriously hampered all upgrade- and
replacement plans.
Anyway, the India Airforce is very powerful, and very divers in it's fighter/bombers.
I'am not sure whether that diversity is a "plus" or a "min", but some jets have very
specific capabilities, like the undisputed nuclear role of the Mirage 2000.
For the current jets, that form the core of the fighter/bombers, here are some
rather unreliable numbers (+ or - 20% or something):
Table: fighter/bomber jets.
| Type: | Number: |
| Mirage 2000: | at least 40 |
| Rafale: | at least 36 were recently ordered. 106 in total? |
| Sukhoi Su-30: | at least 240 |
| Mig-29: | at least 70 |
| Mig-27: | 50? (not sure at all) |
| Mig-21: | around 110 |
| Jaguar SEPECAT: | around 90 |
| Tejas LCA Mark-I: | 16 (for now) |
Next to this list, nummerous support-, transport-, surveillance-, patrol-, heavy lift-,
and various other planes, are part of the Indian Airforce.
You may wonder why my listing has a rather high uncertainty.
- First, many upgrades (instead of replacements) seemed to be planned, but nothing
seems certain here.
- Replacements by "what", also seems not fully certain here. The order of the Rafale
looks pretty certain, but for others it did not became clear to me, even while I invested
quite some time trying to figure it out.
For nuclear capable jets for free fall nuclear devices: the Mirage is certain for that role.
The SU-30 MKI is suitable as well. For cruise missiles like the Nirbhay, Brahmos
likely multiple candidates exists. The SU-30 MKI is a candidate for sure.
5.5.2.4. Some further remarks on the Indian Navy:
We have seen that the Airforce is no less than enormous. Now, what about the Indian Navy?Rather enormous too! It's actually one of the most powerful Navy's on the Planet.
For the scope of this note, it's unneccessary to list every detail of a Frigate or any
other vessel. But highlighting the number, and types of vessels, is important, to
appreciate the power of the Indian Navy.
-It's likely that some models will be equiped with the "Dhanush" or similar
nuclear enabled cruise missiles.
-In principle, any modern frigate/destroyer, can be fitted for the Bhramos cruise missile.
The Bhramos can be fitted on multiple mountpoints/launching systems, like e.g. VLS.
-OLD frigates/destroyers: Some older frigates/destroyers came (modified) from the
Russian Federation. As far as I found, none were fitted with e.g. P700 Granit series,
P800 Onyx (Oniks) series, or similar older systems, or modern Russian cruisemissiles
(except the jointly developed Bhramos, and the Russian Kh-35).
-NEW frigates/destroyers: End 2018, early 2019, contracts were signed for building
4x modern frigates, by the Russian Federation. These frigates will be equiped with an arry of
"state-of-the-art" Russian weaponry, including the Kalibr (klub/export) cruise missile.
These are likely to be the Admiral Grigorovich class, or project 11356 vessels.
-The existing Talwar class (6 vessels), and various others, uses the export (klub) Kalibr
missile too.
Subs:
-Arihant class Nuclear-Powered Ballistic Missile submarines and armament:One operational, one beginning seatrials around 2020, 2 or 4 more planned for the late 2020's
-Leased Nuclear powered Russian Akula class attack subs:
At least one operational, possible we have 2x Akula class subs operational.
-Conventional subs, non-nuclear, no nuclear weapon systems.:
These are models in the Kalvari class, Sindhughosh class, and Shishumar class subs.
In total, we seem to have 12 - 15 vessels here.
Frigates/Destroyers (typically 3000 - 7000 ton) - Blue Navy:
| Type: | Number: |
| Recently, Russia and India signed contracts in November 2018, on the delivery of 4x Project 11356 frigates. These will include a variety of modern weapon systems, including the Kalibr (klub export) cruise missiles. These are likely to be the Admiral Grigorovich class, or project 11356 vessels. |
at least 4 for > 2024 |
| The modern Kolkata class: frigates/destroyers, 3 in service, as of 2014-2016. |
3 in service |
| Delhi class: destroyers, 3 in service, as of 1990-2000. | 3 in service |
| Rajput class: destroyers, 4 in service, as of 1980-1988. | 4 in service |
| Talwar class: Frigates, as of 2003. Uses the Kalibr (klub export) cruise missiles |
at least 3 in service |
| Godavari class: Frigates, as of 1983. Probable candidate to phase out. |
1 in service |
| Shivalik class: Frigates, as of 2010. Uses the Kalibr (klub export) cruise missiles. |
3 in service |
| Brahmaputra class: Frigates, as of 2000. Uses the Kh-35 (SS-N-25) or Kh-35E cruise missiles. |
3 in service |
Corvettes and support vessels (landing-, transport-, patrol vessels etc..) - Green Navy.
An enormous collection of green water Corvettes, and various support vessels,are part of the Indian Navy. It's not needed for the scope of this note,
to go into any detail.
5.5.2.5. ABM: Anti Ballistic Missile systems:
ABM systems are considered to be a vital element in defence, and may function asa part in "deterrence" too. Or..., is nowadays the Defence role a bit overstated?
Modern problems for ABM systems:
The Russian Federation is capable of using hypersonic cruise missiles, or ballistic missilesusing an irregular, unpredictable, virtual path. For such systems, it is realistic to say that
ABM systems have a very low probability to neutralize such missiles.
Note: Ofcourse, you might say, that an "Anti Ballistic Missile" systems, is designed to counter
"Ballistic missiles" in the first place, and not specifically against cruise missiles.
That's right.
It must be understood that the term "ABM", indeed, for all practical reasoning, applies to
intercepting ICBM's and MRBM's/SRBM's only, and thus not for other systems like cruise missiles.
For ICBM/MRBM and similar, once out of a exo atmospheric ballistic path, and later entering the
decent stage, speeds might be in a range of mach 15 - mach 20 in the terminal phases,
which may be considered to be untouchable too.
Ofcourse, once in relevant atmospheric resistance, speeds may diminish a bit, but often still remain
in the mach 8 - mach 10 range, or even much faster.
However, relatively short after launch, and nearing, or crossing a LEO trajectory, the missiles
might be prey to ABM systems. This might also be true, in the first phases of decent.
But "Avangard" and related technolgies, will enable irregular, unpredictable paths, meaning
that in any phase during decent, the warheads are again pretty much untouchable.
-Some ABM systems are designed for a max plafond of say 20, 30, 50, 70 km. Others are exo-atmospheric
and may reach heights of 100, 150, 200 km.
-Some ABM systems (1) fully rely on impact with the incoming device (destroy by kinetic energy),
while (2) on the other end of the spectrum, the ABM system uses a nuclear detonation which may
destroy the incoming devices (for example, Russian systems near Moskow).
(3) Most systems ABM systems however, use HE fragmentation charges to eliminate missiles.
It's probably fair to say that for modern incoming threats, ABM systems generally have a rather
low success rate. Ofcourse, that's a general statement, and it also depends on the type
of system and origin (manufacturer).
Remarkably, the ABM systems of India, are pretty good, at least for about targets with a precise
trajectory, and thus interception is in principle possible, given a correct tracking mechanism.
See below.
Anti Ballistic, or Anti Satellite?:
A Low Earth Orbit (LEO), starts as of (around) 180km altitude. That low altitude, does not allow anyobject to orbit Earth for a long time.
As from 300km altitude (or so), orbits become more stable. The International Space Station (ISS),
orbits the Earth at an altitude of around 440km.
LEO is characterized by altitude between 180km - 2000km. A Mid Earth Orbit (MEO) is charcterized by
an altitude of 2000km - 35780km.
A sattelite could for example, orbit in a (near) circle around Earth with an altitude of say 700km.
It could als have a very excentric orbit (elliptical), with a near point to Earth of several hundreds
of km, and the far point many thousands km away.
There are many options here, and it's all a matter of Pure Physics.
A "test" sattelite, brought in orbit to test an ABM system, could have any altitude, given that it's
still relatively near Earth, like 180km, 200km, or maybe even 300km etc..
By the way, a Chinese test in 2007, used an object with an altitude way over 500km.
Ballistic missiles often follow a sort of skewed parabolic path. ICBM's generally follow a long arc,
and with some "fantasy", you may see a rather "flat" skewed parabolic as well. However, the last stage
of a modern missile containing the Warheads in MIRV, most often have small thrusters to position
the that last stage according to it's mission.
It's true that older ICBM last-stages, follows a free-motion arc, with it's highest altitude (apogee) somewhere
around 2000km - 2500km (or somewhat higher or lower), and subsequently enters the decending stage.
March 2019: India destroys a satellite in low-orbit Space:
Around march 26, 2019, India managed to destroy one of it's own satellites (probably MicroSat-R),
at an altitude of near 300km.
While that is a monumental achievement, it still was an object with a precise and thus predictable trajectory.
Shooting a satellite is often called ASAT (anti-satellite technology).
With that landmark, India placed itself among countries which have managed more or less the same:
China, USA, and the Russian Federation.
It can be argued that Israel manages such technology too, but formally seems not to be "on the list".
This step of India, might be interpreted as a signal to China and Pakistan, and possibly even was
highly motivated by the Indian elections which were soon taking place, in order to enhance
the popularity of Pres. Modi.
By the way, killing satellites in this manner, creates debri, which poses a real threat to
other spacecrafts, including manned spacecrafts.
Luckily, this satellite was in lower LEO (300km altitude), so much of the debri will burn-up
in the atmosphere the coming months.
Anyway, the test succeeded.
This ASAT event, can also be seen as an advanced ABM test, but ofcourse the target was an object
having a precise trajectory.
The target was destroyed using kinetic impact, and not using HE fragmentation. It could wel be
that metal strips targeted the satellite, and completely destroyed it due to high kinetic impact.
I have not certainty about the missile itself, but it's possibly an improved AD-1/AD-2 missile.
ABM systems:
⇒ inner atmospheric, or "endo-atmospheric": AAD and PAD
It's actually a complementary system, to cover atmospheric targets (meaning "in" the atmosphere,
or "endo-atmospheric"), called the AAD system, and the PAD system.
Advanced Area Defence (AAD system missile) is an atmospheric missile, capable of intercepting
incoming targets at an altitude of up to 30 km.
What is remarkable, is the fine grained targeting radars involved, and optical devices, which makes a
high hitrate possible against traditional ballistic targets.
PAD is the system that operates against targets while still having an altitude of around 80km.
For lower altitudes like 30km, then AAD comes into play.
AAD: up to 30km
PAD: up to 80km
⇒ outer atmospheric, or "exo-atmospheric": AD-1 and AD-2
This is covered by the AD-1 and AD-2 missile systems. These are high-end hypersonic missiles,
capable to operate well above the atmosphere.
⇒ inner atmospheric / outer atmospheric.
India also purchased S300 (some time ago) and S400 systems (relatively recent).
These come in a multitude of variants. Some variants are explicitly suitable
to perform an ABM role.
I personally have no doubt that the S500 will be ordered too, once the export models have
become fully operational.
For now: section 5.5 is done.
Sofar about Pakistan and India. New information, or updates, will be placed in this section.
I most certainly do not pretend to be complete on the subject. Far from it !
However, for a simple "impression" about the current capabilities, it might have some value.
5.6 An attempt to say something on the Nuclear capabilities of NK.
This is quite a special project, as I see it, for me personally.Ofcourse, as for most folks, NK is a sort of Black Hole, and not much info (seems to be)
available, for how far their nuclear capabilities goes.
As might be expected, "vagueness" rules here. There is no reliably number to be found.
Only "estimates" go around, which also vary considerably (like min=5, max=60 for operational devices).
A number of "60" is absolutely unrealistic. But what are reasonable intervals then?
I will use two approaches: (1): a weighted interval, derived from reasonable reports,
and (2): an approach that will also take into account failed detonations 2006-2013.
I can imagine that you skip this chapter, since you probably do not like BS anyway.
My findings:
One thing seems quite obvious: since quite some time, NK tried to develop a fission weapon, but
they seemed to be enormously handicapped with the correct "timing issues" around the
implosion technique, and probably also by insufficiently high enough "% high-grade" U235 or Pu, which likely
produced a number of "fizzles" in the first decade of the 2000's.
If an implosion by the outer shell is not near perfect, some parts compress the pusher faster
than other parts, where the effect then will be that the symmetry will be completely spoiled, and
and just a very partial amount of fission occurs, which will produce a detonation of an extremely
low yield.
I am also not saying that there was not "enough" U235 or Pu, but it has to be near 90% or better,
unless your other parameters are near perfect (geometry, reflectors etc..).
This is my theory, which deviates somewhat from the wiki's etc.., which you can find everywhere.
If you have read some chapters above, many factors play a role to start an overall "superfast" rate
of fission (e.g. geometry, critical mass, neutron reflectors, initial flux etc.., and a near
perfect spherical implosion to uniformly compress the subcritical parts into supercritical etc..).
Possible origins of the nuclear capabilities:
It's an extensive, and interesting, and sometimes "vague" history of the origins of NK'snuclear capabilities. There is no shortage of info to someone who would write a 500 page book
on all events, and all speculations, and historical facts, and who was involved.
There was some early involvement of the Sovjet Union, when nuclear research seemed to be
a rather legitimate option at that time (early '60's), and much later, by Pakistan, where
Kahn supplied vital information on procedures on how to enrich Uranium.
This whole history is quite interesting, but I like to refer the reader to other and
more appropriate sites, to learn more.
The are many places to find historical info. One such place might be:
Chronology of U.S.-North Korean Nuclear and Missile Diplomacy (armscontrol.org)
It's I think a good chronology of important facts, but maybe a tiny bit "coloured" from a
Western point of view. But I'am not even sure of that, and I don't want to do it unjustice, but it seems that way.
Current number of nuclear devices, 2018/2019: According to reports, and what I believe.
This is ofcourse the key information. Many reports have been published, on estimates onthe number of operational devices, and estimates of high-grade U235 or Pu, which allows NK to produce
other devices in a relatively short time. Those estimates vary considerably.
These are like min=5 and max=60 for operational devices. For a weighted mean when considered all
reasonably trustworthy reports, it seems to be around 15 for truly operational devices.
In my (rather superfluous) investigations, I can tell you the following:
I only used articles of institutions which have at least some scientific backing, and which seem
to be independent from Agencies, Governments and such stuff.
- The min/max numbers of operational devices, along all reports, are between 5 and 60.
- A weigted mean along all reports would deliver a number around 15 for operational devices.
As at seems, when studying different reports:
⇒ Around 15 for operational devices.
Deviations:
When considering the timeline during all tests, and considering/assuming a number of "fizzles"
at the first testphases, I propose a different interval. First, please notice that the idea
of fizzles (failed explosions) seems not to be taken into considerations, at official reports.
My proposal then would be (for up until 2018/2019):
⇒ Any number between 5 and 13. It looks like that 7 might be a reasonable estimate.
You may doubt that, or completely reject it. It's based on my own reasoning.
Rough timeline of possible nuclear tests.
-October 9, 2006: North Korea conducts the very first underground nuclear test near P'unggye.Seismic data collected by SK, Japan, and US, a yield around, or just below, one kiloton was observed.
It has every characteristic of a fizzle to me.
You may assume further, that for the first serious test, NK used enough U235 or Pu for a reasonable
large effect. Certainly "first time", since experience with boosting, geometry etc.. was not yet
available.
Unless you would believe that they were targeting for a 1 kT yield. It's unlikely.
-May 25, 2009 North Korea conducts the second underground nuclear test near P'unggye.
Seismic data indicates a yield of around, or just below, 4 kiloton.
Improved detonation, still rather small, indicating a non perfect spherical implosion,
possibley in combination with insufficiently % highgrade fissile material, and/or
in combination with a failed geometry of supporting elements (e.g. reflector, initial flux etc..).
Indeed, still characteristic of an imperfect nuclear detonation, as a fairly good fizzle.
-February, 12 2013: North Korea conducts the third underground nuclear test near P'unggye.
Finally, a succesful nuclear detonation. Seismic data indicates a yield of around, 6 to 14kT.
I believe that 12 Februari 2013, marks the final day of a first complete nuclear test, based on pure fission.
In the period thereafter, over a few years, some other tests followed.
At some moment, januari 2016, NK claimed a test of a H bomb. This is most certainly NOT a true multistage
thermonuclear device.
However, it's very likely, that they finally mastered the "boosting" principle,
using Lithium Deuteride, or small amounts of Li6, with small amounts of Tritium and Deuterium.
Indeed, the last test was very powerful, often estimated to be in the range 60 to 110kT.
The timeline of 2006, up to 2013, resulting in the first practical fission weapon, indicates the
"hard time" or struggle of NK, "to get it right".
Based on this, and other intel, like that NK is on a hold for further production since the
first talk with Pres. Trump, and the strong sanctions, and the fact the NK already partially has
cleared some important testsites.
About the number 7 (interval 5-13): The "7" is sort of "weighted", since ofcourse mathematically the number
"9" would fit the interval better. However, I have better faith in the interval [5-13], than in some
fixed number, like 7 or 9 etc..
Let's see if we can find someting usable about the "anatomy" of their devices.
Then after that, I will try to list a representable table of current ballistic missiles.
I already did some work. It seems that NK is quite mature in all sorts of ballistic missiles.
However, I believe that they do NOT have a full ICBM yet (2018/2019), wich will cross LEO,
at some point, and then on re-entry of the warhead in the atmosphere, can survive a mach 8 - mach 20
terminal velocity on the final decend.
Possible anatomy.
Ballistic missiles.
Conventional weapon systems.
5.7 Main current nuclear weapons of China (People's Republic of China).
I had my text on China ready, but on a recent close inspection,
it simply was not good enough. I have to redo that text.
5.7.1 Current ICBM/MRBM/SRBM (landbased).
5.7.2 Current Strategic Bombers.
5.7.3 Current SLBM's and nuclear submarines.
5.7.4 Current nuclear capable Cruise missiles.
5.7.5 Other nuclear capable elements (Navy, Airforce, Army, UAV's)
5.8 Main current nuclear weapons of the USA.
5.8.1 Current ICBM/MRBM/SRBM (landbased).
5.8.2 Current Strategic Bombers.
5.8.3 Current SLBM's and nuclear submarines.
5.8.4 Current nuclear capable Cruise missiles.
5.8.5 Other nuclear capable elements (Navy, Airforce, Army, UAV's)
Appendix 1: Materials in Nuclear Technology.
It helps to get a good idea on how the Uranium and Plutonium isotopes are aquired, and howUranium imports/exports go around. Also, how much of those isotopes is available for all
nuclear capable countries? This is an important question too.
I am afraid that this is going to be a rather lengthy chapter in this note.
So, let's see what we can find here.
First, let's consider some important elements/isotopes needed in the nuclear business.
⇒ 6.1 Beryllium:
This is the fourth element in the well-known Periodic Table, which starts with H (Hydrogen), He (Helium),Li (Lithium), Be (Beryllium) etc.. The isotope 94Be is a stable isotope.
⇒ The application in nuclear devices:
The most important application in nuclear weapons, is the implementation as a "reflector" of neutrons.
A fissile core, often multiple parts, is surrounded by conventional explosives, and this structure will be
again surrounded by the (often spherical) reflector made of Beryllium.
The conventional explosion compresses the parts of the fissile material (like Pu).
When fission starts to become relevant (all measured in μsec), outbound neutrons will be partly
reflected back (scattering) into the core, again contributing to the fission process.
As anoher usage in the same configuration, it will act as a tamper (for an extremely short period), which
keeps the core together until fission reaches a point with too much heat and pressure. However, the fisson
has become very efficient by now, and the superfast detionation follows.
Beryllium is thus an important element in modern weapon architectures.
⇒ Mining and production of Beryllium:
Beryllium is very strong, stiff, and has a relatively high melting point temperature (2349F).
Beryllium looks like darkgrey metallic stuff, and is extremely light in weight (e.g. compared to Aluminium).
Various Beryllium alloys have also a growing application in e.g. micro electronics, due to very good
performances like heat dissipations etc.. But in various other sectors alloys are applied.
It's expected to be a growing market.
Beryllium, and several alloys and compounds, are very toxic and can only be handled using strict procedures.
Most of the Beryllium ore is found and processed in the US. Second comes China, and thereafter follows
Brazil, and some countries in Africa (Mozambique). In Russia and Kazachstan production once was low, but was
picked up again aroud 2011.
Two main minerals, bertrandite and beryl, are mined for beryllium. To actually produce Beryllium, a lengthy
and costly procedure is followed.
Currently, only three countries, which are the US, China and Kazakhstan, seems to process beryllium ores
into the metal and various Alloys/Compounds.
⇒ Some main mining/processing companies:
Important: I am not fully sure of the accuracy of the listing below.